Скалярное произведение в координатной форме

§7. Скалярное произведение в координатной форме. 

      Пусть векторы a  и  b  заданы своими координатами в ортонормированном базисе { i,  j,  k }:

 и  . Умножая скалярно a  на  b, получим

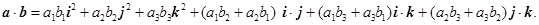
 Для выбранного базиса выполняются соотношения:   Отсюда

Рекомендация для Вас - 2.4 Собирание славянских земель и расцвет Киевской Руси.

получаем:   −   Скалярное произведение в ортонормированном базисе

равно сумме попарных произведений координат.

Таким образом, имеем:        

Пример. Вычислить длины векторов и косинус угла между ними: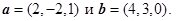

{}              

Замечание.  В косоугольном базисе формула для выражения скалярного произведения через координаты будет, естественно, отличаться.