Случайные функции

5. Случайные функции

5.1 Характеристики случайных функций

Случайная функция – функция, которая в результате опыта может принять тот или иной неизвестный заранее конкретный вид. Обычно аргументом случайной функции (с.ф.) является время, тогда с.ф. называют случайным процессом (с.п.).

С.ф. непрерывно изменяющегося аргумента t называется такая с.в., распределение которой зависит не только от аргумента t=t₁, но и от того, какие частные значения принимала эта величина при других значениях данного аргумента t=t₂. Эти с.в. корреляционно связаны между собой и тем больше, чем ближе одни к другим значения аргументов. В пределе при интервале между двумя значениями аргумента, стремящемся к нулю, коэффициент корреляции равен единице:

,

т.е. t₁ и t₁+Dt₁ при Dt₁®0 связаны линейной зависимостью.

С.ф. принимает в результате одного опыта бесчисленное (в общем случае несчетное) множество значений – по одному для каждого значения аргумента или для каждой совокупности значений аргументов. Эта функция имеет одно вполне определенное значение для каждого момента времени. Результат измерения непрерывно изменяющейся величины является такой с.в., которая в каждом данном опыте представляет собой определенную функцию времени.

С.ф. можно также рассматривать как бесконечную совокупность с.в., зависящую от одного или нескольких непрерывно изменяющихся параметров t. Каждому данному значению параметра t соответствует одна с.в X_t. Вместе все с.в. X_t определяют с.ф. X(t). Эти с.в. корреляционно связаны между собой и тем сильнее, чем ближе друг к другу.

Элементарная с.ф. – это произведение обычной с.в. Х на некоторую неслучайную функцию j(t): X(t)=X×j(t), т.е. такая с.ф., у которой случайным является не вид, а только ее масштаб.

Рекомендуемые материалы

С.ф.  - имеет м.о. равное нулю. p[x(t₁)] – плотность распределения с.в. Х (значения с.ф. X(t)), взятой при произвольном значении t₁ аргумента t.

Реализация с.ф. X(t) – описывается уравнением x=f₁(t) при t=t₁ и уравнением x=f₂(t) при t=t₂.

Вообще функции x=f₁(t) и x=f₂(t) – различные функции. Но эти функции тождественны и линейны тем более, чем более (t₁®t₂)  t₁ ближе к t₂.

Одномерная плотность вероятности с.ф. p(x,t) – зависит от х и от параметра t. Двумерная плотность вероятности p(x₁,x₂;t₁,t₂) – совместный закон распределения значений X(t₁) и X(t₂) с. ф. X(t) при двух произвольных значениях t и t¢ аргумента t.

 .                          (66.5)

В общем случае функция X(t) характеризуется большим числом n-мерных законов распределения .

М.о. с.ф. X(t) - неслучайная функция , которая при каждом значении аргумента t равна м.о. ординаты с.ф. при этом аргументе t.

 - функция, зависящая от x и t.

Аналогично и дисперсия - неслучайная функция.

Степень зависимости с.в. для различных значений аргумента характеризуется автокорреляционной функцией.

Автокорреляционная функция с.ф. X(t) - неслучайная функция двух аргументов K_x(t_i,t_j), которая при каждой паре значений t_i, t_j равна корреляционному моменту соответствующих ординат с.ф. (при i=j корреляционная функция (к.ф.) обращается в дисперсию с.ф.);

                  (67.5)=(34.3),

где  - совместная плотность распределения двух с.в. (значений с.ф.), взятых при двух произвольных значениях t₁ и t₂ аргумента t.  При t₁=t₂=t получаем дисперсию D(t).

Автокорреляционная функция - совокупность м.о. произведений отклонений двух ординат с.ф. , взятых при аргументах t₁ и t₂, от ординат неслучайной функции м.о. , взятых при тех же аргументах.

Автокорреляционная функция характеризует степень изменчивости с.ф. при изменении аргумента. На рис. видно, что зависимость между значениями с.ф., соответствующим двум данным значениям аргумента t - слабее в первом случае.

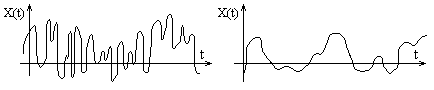
Рис. Корреляционно связанные случайные функции

Если две с.ф. X(t) и Y(t), образующие систему не являются независимыми, то тождественно не равна нулю их взаимная корреляционная функция:

                (68.5),

где  - совместная плотность распределения двух с.в. (значений двух с.ф. X(t) и Y(t)), взятых при двух произвольных аргументах (t₁ - аргумент функции X(t), t₂ - аргумент функции Y(t)).

Если X(t) и Y(t) независимы, то K_XY(t₁,t₂)=0. Система из n с.ф.  X₁(t), X₂(t),...,X_n(t) характеризуется n м.о. , n автокорреляционными функциями  и еще n(n-1)/2 корреляционными функциями .

Взаимная корреляционная функция (характеризует связь между двумя с.ф., т.е. стохастическую зависимость)  двух с.ф. X(t) и Y(t) - неслучайная функция двух аргументов t_i и t_j, которая при каждой паре значений t_i, t_j равна корреляционному моменту соответствующих сечений с.ф. Она устанавливает связь между двумя значениями двух функций (значения - с.в.), при двух аргументах t₁ и t₂.

Особое значение имеют стационарные случайные функции, вероятностные характеристики которых не меняются при любом сдвиге аргумента. М.о. стационарной с.ф. постоянно (т.е. не является функцией), а корреляционная функция зависит лишь от разности значений аргументов t_i и t_j.

,                                 (69.5)

Это четная функция (симметрично OY).

Из (69.5)® .

При большом значении интервала времени t=t₂-t₁ отклонение ординаты с.ф. от ее м.о. в момент времени t₂ становится практически независимым от значения этого отклонения в момент времени t₁. В этом случае функция K_X(t), дающая значение корреляционного момента между X(t₁) и X(t₂), при ½t½®¥ стремится к нулю.

Многие стационарные с.ф. обладают эргодическим свойством, которое заключается в том, что при неограниченно возрастающем интервале наблюдения среднее наблюденное значение стационарной с.ф. с вероятностью, равной 1, будет неограниченно приближаться к ее м.о. Наблюдение стационарной с.ф. при разных значениях t на достаточно большом интервале в одном опыте равноценно наблюдению ее значений при одном и том же значении t в ряде опытов.

Иногда требуется определить характеристики преобразованных с.ф. по характеристикам исходных с.ф. Так если

                                                             (70.5),

то  т.е. м.о. интеграла (производной) от с.ф. равно интегралу (производной) от м.о. (y(t) - скорость изменения с.ф. X(t),  - скорость изменения м.о.).

При интегрировании или дифференцировании с.ф. получаем также с.ф. Если X(t) распределена нормально, то Z(t) и Y(t) распределены тоже нормально. Если X(t) – стационарная с.ф., то Z(t) уже не стационарная с.ф., т.к.  зависит от t.

Примеры корреляционных функций.

1)  (из (2) при b®0);                      2) ; 

3) ;                                                      4) ; 

5) (из (3) при b®0);                                      6)  (из (4) при b®0).

На графиках a = 1, b = 5, s = 1.

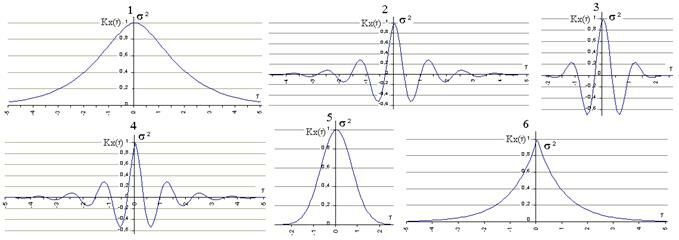
a - характеризует быстроту убывания корреляционной связи между ординатами с.ф. при увеличении разности аргументов этих ординат t.

a/b - характеризует "степень нерегулярности процесса". При малом a/b ординаты процесса оказываются сильно коррелированными и реализация процесса похожа на синусоиду; при большом a/b периодичность с частотой b становится незаметной.

Корреляционные функции 4 и 6 – не имеют производных при t=0. Соответствующие спектральные плотности:

2) ;

3) ;

4) ;

6) .

Чтобы найти корреляционную функцию интеграла (производной) от с.ф., нужно дважды проинтегрировать (продифференцировать) корреляционную функцию исходной с.ф. сначала по одному, затем по другому аргументу:

                                                      (71.5).

Формула (71) для стационарной функции примет вид:

.

Корреляционная функция с.ф. и ее производной . Для дифференцируемого стационарного процесса ордината с.ф. и ее производной, взятая в тот же момент времени являются некоррелированными с.в. (а для нормального процесса и независимыми).

При умножении с.ф. на детерминированную получаем с.ф. Z(t)=a(t)X(t), корреляционная функция которой равна

K_Z(t₁,t₂)=a(t₁)a(t₂) K_X(t₁,t₂)                                                     (72.5),

где a(t) - детерминированная функция.

Сумма двух с.ф. является тоже с.ф. Z(t)=X(t)+Y(t) и ее корреляционная функция при наличии корреляционной связи между X(t) и Y(t):

K_Z(t₁,t₂)=K_X(t₁,t₂)+ K_Y(t₁,t₂)+2K_XY(t₁,t₂),                                        (73.5)

где K_XY(t₁,t₂) - см. (68.5) - взаимная корреляционная функция двух зависимых с.ф. X(t) и Y(t).

Если X(t) и Y(t) независимы, то K_XY(t₁,t₂)=0.     М.о. с.ф. Z(t):       .

5.2. Выбросы случайной функции за заданный уровень

Необходимость определения вероятностных характеристик процесса пересечения с. функцией заданного уровня возникает, когда необходимо вычислить вероятность того, что в течение срока службы нагрузка, действующая на строительную конструкцию, не превысит допустимого уровня. Найдем вероятность пересечения случайной функцией (дифференцируемой) X(t) некоторого уровня а в течение времени t. Полагая скорость изменения с.ф. V(t)=dX(t)/dt постоянной в течение времени dt (с точностью до бесконечно малых второго порядка) условие пересечения функцией X(t) уровня а за малый промежуток времени dt:

X(t)<a; X(t)+V(t)dt>a                                                            (74.5)

или

a-V(t)dt<X(t)<a (V(t)>0)                                                    (75.5).

Вероятность этого события (выраженного условием (75)):

                                                       (76.5),

где p(x,V) - совместная плотность распределения с.ф. X(t) и V(t).

Ввиду близости пределов внутреннего интеграла (его заменили на p(a,V)Vdt - площадь прямоугольника) вероятность выброса:

                                                         (77.5).

Если разделить вероятность выброса Q_a на время dt, в течение которого он ожидается, получится временная плотность вероятности выброса за уровень а в момент t (среднее число выбросов в единицу времени):

                                                             (78.5).

В случае стационарного с.п. X(t) и Y(t) - независимые с.ф. и (при том  и известна автокорреляционная функция для X(t) - K_X(t)), следовательно,

p(x,V)=p_x(x)×p_V(V),                                                              (79.5)

где p(x,V) - совместная плотность распределения X(t) и Y(t); p_x(x)×и p_V(V) - соответственно плотности распределения X(t) и Y(t).

Тогда временная плотность вероятности выброса:

                                        (80.5),

где  - м.о. положительной скорости V(t).

Для нормального распределения X(t):

                                                      (81.5)

распределение скорости V(t) будет также нормальным и независимым от распределения X(t):                                                           (82.5).

М.о.  вследствие стационарности процесса. По (72) .

Подстановка (82) и (81) в (80) даст для временной плотности вероятности выброса

                                                   (83.5).

Доказательство (83.5):

.

Заменим подынтегральное выражение,

,

 тогда

,

и тогда .

Чем больше уровень а, тем меньше q(a). При очень малом значении q(a) выбросы можно рассматривать как редкие события, т.е. как независимые с.в.

Если число выбросов в течение времени t подчиняется закону Пуассона  (66), тогда вероятность того, что за время T не произойдет ни одного выброса при условии, что X(t) – стационарная функция

P_t=exp[‑q(a)T]                                                                 (84.5)

Это функция надежности.

В случае нестационарной функции

                                                                   (85.5).

6. Приближенные методы нахождения распределения функций с.в.

6.1 Метод Монте-Карло (метод рандомизации)

Есть система двух с.в. X и Y и p(x,y) – совместная плотность их распределения. Данный метод позволяет найти плотность распределения p(U), где U=U(X,Y).

Для одномерной с.в. Х, где р(х) – плотность ее распределения, можно найти p(U), причем U есть функция от X:

U=U(X)).

Суть метода в том, что аргументам X и Y даются случайные значения, распределенные согласно p(x,y). Случайные числа для значений аргументов можно брать по таблицам (есть таблицы для равномерного, нормального распределений, распределения Пирсона и т.д.) или определять на ЭВМ по специальной программе. Каждой случайной точке (x_i,y_j) соответствует определенное значение функции U(x_i,y_j). После реализации достаточно большого количества значений с.в. U их можно сгруппировать по интервалам nD<U<(n+1)D и построить ступенчатую аппроксимацию искомой кривой распределения p(U). Метод эффективен при использовании ЭВМ и при разрывности функции U(X,Y) (или при различном ее аналитическом описании в различных областях плоскости XOY).

Если есть функция двух с.в. U=U(X,Y) и p(x,y) – совместная плотность распределения X и Y, то

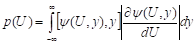
(получено из (40.3) и (29.3)), где x=y(U,y).

                                                                  (86.6)

и

                                                       (87.6),

Вместе с этой лекцией читают "9 Направления оперативной организации ДД".

но для двух аргументов.

6.2 Метод статистических испытаний

Производится достаточно большое число статистических испытаний по схеме Бернулли, т.е. на каждом испытании генерируются случайные реализации всех исходных величин. Далее, например, если необходимо определить вероятность отказа системы, то испытания проводятся n раз, и каждый раз проверяется условие наступления отказа (например, Q>R, где Q – фактическая нагрузка на систему, R – прочность системы). Затем частота появления отказа: P*(A)=m/n, где m – количество отказов. При n®¥ -

P*(A)®P(A),

где P(A) – вероятность наступления отказа, являющаяся достоверной величиной.

В данном методе необходимо оценить погрешность определения P*(A) при определенном количестве испытаний n¹¥ или оценить количество испытаний n, необходимое для достижения частотой наступления отказа P*(A) достаточной достоверности.