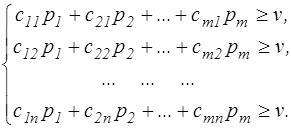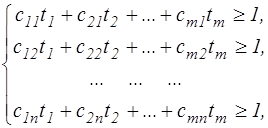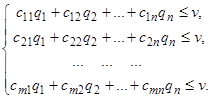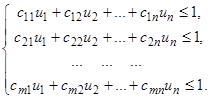Основные понятия
Тема 9 Игровые методы обоснования решений
Основные понятия
Одна из задач теории оптимальных решений - принятие решения в условиях неопределённости. Для обоснования решений разработаны специальные математические методы, которые рассматриваются в теории игр. Теория игр принадлежит к наиболее молодым математическим дисциплинам. В 1927 г. французский математик Э. Борель сформулировал "фундаментальную теорему" теории игр - теорему существования оптимальных стратегий, которую в 1928 г. доказал Дж. фон Нейман. А в 1944 г. появилась капитальная монография по теории игр Дж. фон Неймана и О. Моргенштерна "Теория игр и экономического поведения". В дальнейшем теория игр превратилось в самостоятельное математическое направление, имеющее практическое применение.
Теория игр - это теория математических моделей конфликтных ситуаций, интересы участников которых различны, причём они достигают своей цели различными путями. Теория игр изучает математические модели так называемых конфликтных ситуаций (т.е. ситуаций, при которых интересы участников либо противоположны и тогда эти модели называются "антагонистическими" играми, либо не совпадают, хотя и не противоположны, и тогда речь идет об "играх с непротивоположными интересами"). Основоположники теории Нейман и Моргенштерн попытались математически описать характерные для экономики явления конкуренции как некую "игру".
В наиболее простом случае речь идет о противоборстве только двух противников, например двух конкурентов, борящихся за рынок сбыта. В более сложных случаях в игре участвуют многие, причём они могут вступать между собой в постоянные или временные коалиции, союзы. Игра двух лиц называется парной; когда в ней участвуют n игроков - это "игра n лиц"; в случае образования коалиций игра называется "коалиционной". Необходимость анализировать такие конфликтные ситуации, в свою очередь, привела к возникновению теорию игр, задачей которой является выработка рекомендаций по рациональному образу действия участников конфликта.
Чтобы исключить трудности, возникающие при анализе практических конфликтных ситуаций в результате наличия многих несущественных факторов, строится упрощенная модель ситуации. Такая модель и называется игрой. Конфликтная ситуация в игровой модели развивается по определённым правилам. Естественной базой для анализа конфликтных ситуаций служат широко распространенные игры - шахматы, шашки, карточные игры. Поэтому теории игр свойственна следующая терминология: "игроки" (стороны, участвующие в конфликте), "выигрыш" (исход конфликта) и т.д.
Суть игры в том, что каждый из участников принимает такие решения (т.е. выбирает стратегию действий), которые, как он полагает, обеспечивает ему наибольший выигрыш или наименьший проигрыш, причём этому участнику игры ясно, что результат зависит не только от него, но и от действия партнера (или партнеров), иными словами, он принимает решения в условиях неопределённости. Неопределённость результата игры вызывается различными причинами, которые можно разбить на три группы, соответственно и классифицируются игры:
1. Особенности правил игры вызывают такое разнообразие в её развитии, что предсказать результат игры заранее невозможно. Источники неопределённости такого вида называются комбинаторными, а соответствующие игры - также комбинаторными. Примером может служить шахматная игра. Однако комбинаторная сложность игр носит исторически преходящий характер благодаря использованию соответствующего математического аппарата и вычислительной техники. (Например, компьютер в шахматы может уже играть в ранге гроссмейстера, а когда-то только на уровне мастера). Для целого ряда комбинаторных игр найдены выигрышные комбинации путём решения логических задач не слишком большого объёма.
2. Другим источником неопределённости является влияние случайных факторов. Игры, в которых исход оказывается неопределённым исключительно в результате случайных причин, называются азартными (игры в кости; игра, состоящая в отгадывании, какой стороной упадет монета; рулетка).
Рекомендуемые материалы
3. Третий источник неопределённости состоит в отсутствии информации о действиях противника, о его стратегии. Игры такого рода называются стратегическими.
Рассмотрим эти игры более подробно. Было уже сказано, что такие игры могут быть парные и множественные. Так как наибольшее практическое значение имеют парные игры, то рассмотрим только их. Участников игры обозначим через А и В. При этом под игрой условимся понимать некоторую последовательность действий (ходов) игроков А и В, которая осуществляется в соответствии с чётко сформулированными правилами. Правила определяют возможные варианты действий игроков, объём информации каждой стороны о действиях другой, результат игры, к которому приводит соответствующая последовательность ходов. В большинстве игр предполагается, что интересы участников поддаются количественному описанию, т.е. результат игры определяется некоторым числом.
Ходом в теории игр называется выбор одного из предположенных правилами игры действий и его осуществление.
Стратегией игрока называется план, по которому он совершает выбор хода в любой возможной ситуации и при любой возможной фактической информации. Естественно, что игрок принимает решение по ходу игры. Однако теоретически можно предположить, что все эти решения приняты игроком заранее. Тогда совокупность этих решений составляет его стратегию. В зависимости от числа возможных стратегий игры делятся на конечные и бесконечные. Задачей теории игр является выработка рекомендаций для игроков, т.е. определение для них оптимальной стратегии.
Оптимальной называется стратегия, которая при многократном повторении игры обеспечивает данному игроку максимально возможный средний выигрыш.
Простейший вид стратегической игры - игра двух лиц с нулевой суммой (сумма выигрышей и проиграшей равна нулю) т.е. один игрок выигрывает столько, сколько проигрывает другой. Игра состоит из двух ходов: игрок А выбирает одну из своих возможных стратегий Ai (i=1,…,m), а игрок В выбирает стратегию Bj (j=1,…,n), причём каждый выбор производится при полном незнании выбора другого игрока. Лучше всего игру продемонстрировать на примере.
Исходные данные игры задаются в виде матрицы выигрышей (или платёжной), все элементы которой положительные. (Любая матрица выигрышей, содержащая отрицательные элементы, может быть преобразована в матрицу с положительными элементами, если все её элементы увеличить на соответствующее положительное число). В этой задаче сторона А имеет три возможные стратегии: А1, А2, А3, сторона В - четыре возможные стратегии: В1, В2, В3, В4. Элемент сij матрицы выигрышей - выигрыш игрока А, если он выбрал стратегию Ai, а игрок В выбрал стратегию Bj. Строки матрицы соответствуют стратегиям Ai, столбцы – стратегиям Bj. Элементы матрицы выигрышей могут быть положительными, отрицательными или равными нулю. Эти элементы определяют суммы, которые сторона В обязана уплатить стороне А в заранее определённой ситуации (AiBj) (это в том случае, когда все элементы платёжной матрицы больше 0).
Таблица 9.1
|
Ai | Bj | Наименьший выигрыш А
| |||
| B1 | B2 | B3 | B4 | ||
| A1 | 35 | 35 | 3 | 10 | 3 |
| A2 | 24 | 1 | 6 | 90 | 1 |
| A3 | 40 | 60 | 10 | 15 | 10 |
| Наибольший проигрыш B
| 40 | 60 | 10 | 90 |
|
Если элемент матрицы отрицателен, то сторона А уплачивает стороне В сумму, равную абсолютному значению элемента. Если элемент равен нулю, то никакой выплаты не происходит. Требуется определить оптимальные стратегии, максимизирующие средний выигрыш правой стороны.
Пусть игрок А выбирает некоторую стратегию Ai; тогда в наихудшем случае (например, если выбор станет известен игроку В) он получит выигрыш, равный  сij. Предвидя такую возможность, игрок А должен выбрать такую стратегию, чтобы максимизировать свой минимальный выигрыш а. Принято говорить, что сторона А руководствуется принципом максиминного выигрыша
сij. Предвидя такую возможность, игрок А должен выбрать такую стратегию, чтобы максимизировать свой минимальный выигрыш а. Принято говорить, что сторона А руководствуется принципом максиминного выигрыша  .
.
То есть сторона А выбирает стратегию А3, которая гарантирует ей наибольший (10) из трёх возможных наименьших выигрышей (3, 1, 10).
Определяемая таким образом величина а называется нижней ценой игры, максиминным выигрышем, или сокращённо максимином. Стратегия  , обеспечивающая получение а, называется максиминной.
, обеспечивающая получение а, называется максиминной.
Если рассуждать аналогично, сторона В выберет стратегию В3, которая гарантирует ей наименьший (10) из четырёх возможных наибольших проигрышей (40, 60, 10, 90).
Принято говорить, что сторона В руководствуется принципом минимаксного проигрыша:  .
.
Величина b называется верхней ценой игры, или минимаксом. Соответствующая проигрышу b стратегия  - минимаксной.
- минимаксной.
 Принцип, который определяет выбор сторонами стратегий, соответствующих максиминному выигрышу или минимаксному проигрышу, часто называют принципом минимакса или принципом осторожности.
Принцип, который определяет выбор сторонами стратегий, соответствующих максиминному выигрышу или минимаксному проигрышу, часто называют принципом минимакса или принципом осторожности.
Если стороны А и В будут использовать принцип минимакса, то выигрыш стороны А составит с33=10. В нашем случае нижняя цена игры а равна верхней цене игры b. В этом случае игра называется вполне определённой, а выигрыш а=b называется значением игры и равен элементу матрицы  .
.
Вполне определённые игры иногда называют играми с седловой точкой, т.к. элемент  в матрице такой игры, являющийся одновременно минимальным в строке i0 и максимальным в столбце j0, и называется седловой точкой платёжной матрицы. Отклонение от неё любой из сторон приводит к уменьшению выигрыша для игрока А соответственно, увеличению проигрыша для игрока В. Седловой точке соответствуют оптимальные стратегии игроков, их совокупность - это решение игры, которая обладает следующими свойствами: если один из игроков придерживается своей оптимальной стратегии, то для другого отклонение от его оптимальной стратегии не может быть выгодно.
в матрице такой игры, являющийся одновременно минимальным в строке i0 и максимальным в столбце j0, и называется седловой точкой платёжной матрицы. Отклонение от неё любой из сторон приводит к уменьшению выигрыша для игрока А соответственно, увеличению проигрыша для игрока В. Седловой точке соответствуют оптимальные стратегии игроков, их совокупность - это решение игры, которая обладает следующими свойствами: если один из игроков придерживается своей оптимальной стратегии, то для другого отклонение от его оптимальной стратегии не может быть выгодно.
В общем же случае фактический выигрыш игрока А при различных действиях партнеров ограничен нижней и верхней ценой игры a£v£b.
Итак, если платёжная матрица содержит седловую точку, то решение игры известно: каждый из игроков применяет свою оптимальную стратегию. Возникает вопрос нахождения решения для игр, матрицы которых не содержит седловой точки. В таких играх а<b. Применение минимаксных (максиминных) стратегий для каждого из игроков обеспечивает выигрыш, не меньший а, и проигрыш, не превышающий b. Для каждого игрока естественен вопрос увеличения выигрыша (уменьшения проигрыша). Решение состоит в том, что игроки применяют не одну, а несколько стратегий. Выбор стратегий осуществляется случайным образом.
Случайный выбор игроком своих стратегий называется смешанной стратегией. В отличие от этого, в играх с платёжной матрицей, имеющих седловую точку, говорят, что решение находится в области чистых стратегий. То есть, если платёжная матрица не имеет седловой точки, то оказывается, что для определения успеха необходимо выбрать стратегии А и В с определёнными вероятностями или частотами при многократной игре, и такие стратегии называются смешанными. Доказано, что для всякой игры с нулевой суммой всегда существуют оптимальные смешанные стратегии. Общее значение верхней и нижней цены называется ценой игры.
Смешанная стратегия для стороны А обозначается:
 ,
,
где p1, p2, p3 - вероятности использования соответствующих чистых стратегий, при этом p1+p2+p3=1.
Смешанная стратегия, которая гарантирует данной стороне наибольший возможный выигрыш (или наименьший проигрыш) независимо от действий другой стороны, называется оптимальной.
Для определения оптимальных стратегий поведения сторон в задачах теории игр используется:
а) с полной информацией - наиболее часто аппарат линейного программирования;
б) с неполной информацией (при наличии некоторого риска) теория игр;
в) при неопределённости - теория стратегических решений.
Таким образом, теория игр тесно связана с такими пограничными областями экономико-математического моделирования, как линейное программирование, теория стратегических решений, и задачи одной области могут переходить в другую и наоборот.
Теперь, когда основные понятия теории игр ясны, рассмотрим общую постановку задачи теории игр.
Постановка задачи и выбор критерия оптимизации
Пусть в игре принимают участие две стороны: А и В. Условия игры заданы платёжной матрицей (см. табл. 9.2 на след.с.).
Таблица 9.2
| A | B | ||||
|
| B1 | … | Bj | … | Bn |
| A1 | c11 | … | c1j | … | c1n |
| … | … | … | … | … | … |
| Ai | ci1 | … | cij | … | cin |
| … | … | … | … | … | … |
| Am | cm1 | … | cmj | … | cmn |
Требуется определить оптимальные вероятности использования стратегий, максимизирующие средний выигрыш первой стороны.
Выбранную стороной А стратегию будем соответственно обозначать А1, А2, …, Аm, аналогично стратегии стороны В – символами В1, В2, …, Bn; pi - вероятность использования стратегии i первой стороной A, qj - вероятность использования стратегии j второй стороной В, при этом  .
.
Построение математической модели
Средний выигрыш первой стороны А:
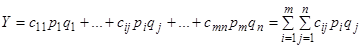
Ограничения:
 .
.
Исследование математической модели
Для получения оптимальных вероятностей использования стратегий А1, …, Аi, …, Аm (B1, …, Bj, …Bn) необходимо взять соответствующие частные производные от целевой функции, приравнять их нулю и решить систему уравнений:
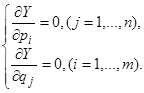
Для примера исследуем матрицу размерности 2х2:
Дана матрица выигрышей.
| Аi | Bj | |
|
| B1 | B2 |
| A1 | с11 | с12 |
| A2 | с21 | с22 |
Требуется определить оптимальные смешанные стратегии:
 .
.
Математическая модель этой задачи:
 ,
,
при этом p1+p2=1, q1+q2=1.
Обозначим р1=р, а р2=1-р, аналогично q1=q; q2=1-q. Подставляя полученные выражения в математическую модель и беря соответствующие частные производные, находим:
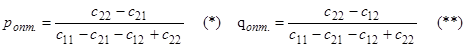
При этом должны выполняться необходимые условия:
0£ропт.£1; 0£qопт.£1.
Значения ропт., qопт., меньшие нуля, необходимо считать равными нулю, а большие единицы - равными единице.
Подставляя оптимальные значения ропт., qопт., 1- ропт., 1- qопт. в целевую функцию Y
 ,
,
получаем максимальный средний выигрыш первой стороны:
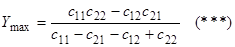
Анализируя эту формулу, видим, что при с11с22-с12с21=0, т.е. с11/с12=с21/с22, игра становится безобидной. Существует так называемая основная теорема теории игр, состоящая в следующем: каждая конечная игра имеет, по крайней мере, одно решение, возможно, в области смешанных стратегий.
Применение смешанной стратегии позволяет получить выигрыш, равный цене игры: а£v£b.
Для оптимальных стратегий игроков имеет место соотношение
 .
.
Применение игроком А оптимальной стратегии  должно обеспечивать ему при любых действиях игрока В выигрыш не меньше цены игры v.
должно обеспечивать ему при любых действиях игрока В выигрыш не меньше цены игры v.
Поэтому должны выполняться следующие соотношения:
|
| (9.1) |
Аналогично, для игрока В оптимальная стратегия игрока  должна обеспечивать при любых стратегиях игрока А проигрыш, не превышающей величину v, т.е. справедливо соотношение:
должна обеспечивать при любых стратегиях игрока А проигрыш, не превышающей величину v, т.е. справедливо соотношение:
|
| (9.2) |
В дальнейшем соотношения (9.1) и (9.2) используются для решения игры. Вообще, задача решения игры, если её матрица не содержит седловой точки, тем сложнее, чем больше значения m и n.
Стратегии игроков А и В, для которых вероятности рi и qj отличны от нуля, называются активными.
Методы решения задач теории игр во многом зависят от условий задачи и от вида матрицы выигрышей первого игрока.
Как уже упоминалось, если матрица С имеет седловую точку, то решение игры сводится к нахождению седловой точки матрицы С. Оптимальные стратегии игроков определяются при этом координатами (i0, j0) седловой точки матрицы С, а цена игры - элементом  .
.
Если матрица С имеет размер mx2 или 2xn, то решение задачи может быть получено графически.
Покажем на примере.
Пример 9.1.
C=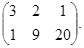
В плоскости переменных (p, v) построим vj(p) - ожидаемый средний выигрыш первого игрока, применяющего первую стратегию с вероятностью р при условии, что второй игрок отвечает чистой стратегией j(j=1, 2, 3):
v1(p)=3p+1(1-p)=2p+1,
v2(p)=2p+9(1-p)=-7p+9, 0£p£1
v3(p)=p+20(1-p)=-19p+20
В точке А пересечения прямых
v1(p) и v2(p) гарантирован-
 v ный выигрыш первого игрока,
v ный выигрыш первого игрока,
 20 изображённой жирной линией,
20 изображённой жирной линией,
достигает наибольшего значе-
с23 ния.
р1+р2+р3=1.

 10 2р+1=7р+9,
10 2р+1=7р+9,


 A 3 с11 9р=8, р=8/9.
A 3 с11 9р=8, р=8/9.
 с22 2 с12
с22 2 с12
 1 P2 P3 р*=(1/9, 1/9); q*=(7/9, 2/9, 0)
1 P2 P3 р*=(1/9, 1/9); q*=(7/9, 2/9, 0)

 с21 1 с13 v*=25/9.
с21 1 с13 v*=25/9.
P1 1-P1 P

 0 1
0 1
Следовательно, игрок А применяет стратегию А1 с вероятностью 8/9, а стратегию А2 - с вероятностью 1/9. Игрок В применяет стратегию В1 с вероятностью 7/9 или В2 с вероятностью 2/9. При этом его выигрыш (игрока А) в среднем составляет 25/9 единиц. Столько же составляет средний проигрыш игрока В.
Пример 2. Найти решение игры, заданной матрицей:
С= .
.
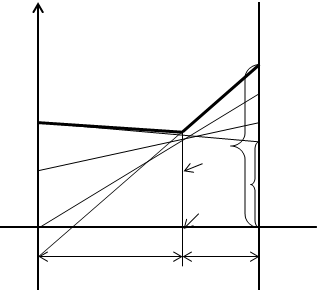
Матрица имеет размерность 4х2, поэтому решение задачи находим для игрока В. Рассматриваем задачу на минимизацию верхней границы проигрыша для игрока В. Следует отметить, что геометрические построения имеют смысл использовать для определения активных стратегий игроков. Затем решение игры можно получить с помощью формул (*), (**) и (***). Формулы эти можно использовать, так как из соответствующей матрицы исключаются все стратегии, кроме активных, и она содержит 2 строки и 2 столбца. Отрезок NK определяет цену игры. Активными стратегиями для игрока А являются первая и четвёртая.
v
 | |||
 | |||
6 А4
5 А3
А1 4 K C42 L 4 А2
3 А1
А2 2 v*
C12
А3 N
0 q2 q1 1 q
-1
q1= q2=
q2= Q*=
Q*= ; p1=
; p1= p2=
p2= P*=
P*= v*=
v*=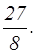
Pешение игр с матрицей mxn, если min{m;n}>2, рассмотрим позднее.
Метод отыскания оптимума функции двух переменных уже в принципе мы рассмотрели - это применение частных производных этой функции и приравнивание их нулю.
Рассмотрим метод Брауна приближённого решения задач теории игр, он подходит и для матриц, размерностью больших 2.
Метод Брауна представляет собой модель практического взаимного обучения игроков, при котором каждый игрок, анализируя способ поведения противника, старается ответить наилучшим способом. Этот метод относится к итерационным, т.е. получающим решение за какое-то количество шагов, причём точность вычисления зависит от числа ходов и от выбора начальной строки.
Первый игрок выбирает одну из своих стратегий. Второй игрок отвечает стратегией, которая минимизирует выигрыш первого игрока. Каждый игрок отвечает на очередной ход противника той своей стратегией, которая является оптимальной относительно всех предыдущих ходов противника.
Рассмотрим решение задачи с матрицей
С= .
.
Первый игрок пусть выбирает i0=3. Второй игрок, просматривая 3-ю строку, выбирает с33=1 – наименьший элемент строки и отмечает его “*”. Справа от матрицы выписываем элементы 3-го столбца. Первый игрок, зная выбор второго и просматривая выделенный столбец, выбирает в нем максимальный элемент (отмеченной звездочкой) и назначает i1=1. Второй строкой под матрицей выписываем суммарный выигрыш первого игрока за 2 хода.
Минимизируя выигрыш первого игрока за два хода, второй игрок выбирает j2=2 и т.д.
Частота выбора строк и столбцов определяет компоненты приближенного решения, элементы со звездочкой определяют суммарный выигрыш за n ходов.
Вычисления в итерационном методе Брауна удобно располагать, как в приведенной таблице:
Таблица 9.3
 2 0 9 6 9* 9 9 9 15 21* 23* 23* 23* 23 23 23 25 28
2 0 9 6 9* 9 9 9 15 21* 23* 23* 23* 23 23 23 25 28
1 3 6 0 6 9* 12* 15* 15* 15 16 19 22 25* 28* 31* 32* 31
4 2 1 3 1 3 5 7 10 13 17 19 21 23 25 27 31 35*
 |
4 2 1* 3 11 12 13 14
6 2* 10 9 В левом верхнем углу записана матрица игры – в данном
7 5* 16 9 случае матрица размера 3х4. Строки ниже матрицы содер-
8 8* 22 9 жат сложенный за n партий возможный выигрыш перво-
9 11 28 9* го игрока, где n – количество партий и номер строки.
10 14 34 9* Столбцы правее матрицы представляют собой сложенный 12* 14 43 15 за n партий возможный проигрыш второго игрока, при-
14 14*52 21 чём n – количество партий и номер столбца. Пусть после 16 14* 62 27 n партий первый игрок обнаружил, что его противник вы-
18 14* 70 33 брал j-ю чистую стратегию (по количеству “звёздочек” в 19 17* 76 33 11 j-м столбце под матрицей) Sj раз (j= ). На этом ос- 20 20* 82 33 12 новании первый игрок допускает, что его противник 21*23 88 33 13 придерживается смешанной стратегии
). На этом ос- 20 20* 82 33 12 новании первый игрок допускает, что его противник 21*23 88 33 13 придерживается смешанной стратегии
22*26 94 33 14
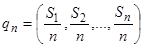
и выбирает в последующей партии чистую стратегию, дающую максимальный средний выигрыш qn. Номер чистой стратегии – это номер максимальной компоненты n-го столбца.
Аналогично, второй игрок после n партий предполагает, что смешанная стратегия соперника  , где ti – частота появления i-й стратегии в предыдущих партиях. В (n+1)-й партии второй игрок выбирает чистую стратегию, обеспечивающую ему минимальный средний проигрыш. Номер этой чистой стратегии – это номер столбца минимального элемента n-й строки.
, где ti – частота появления i-й стратегии в предыдущих партиях. В (n+1)-й партии второй игрок выбирает чистую стратегию, обеспечивающую ему минимальный средний проигрыш. Номер этой чистой стратегии – это номер столбца минимального элемента n-й строки.
Степень приближения к решению зависит от выбора начальной строки и от числа ходов, поэтому:
при n=10 при n=14
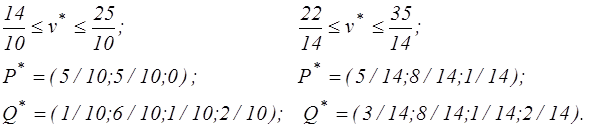
Можно решить задачу теории игр, сведя математическую игру к задаче линейного программирования.
В самом деле, рассмотрим игру, матрица С которой имеет размерность mxn:
C= .
.
Пусть матрица не содержит седловой точки, поэтому решение игры представлено в смешанных стратегиях: Р=(p1, p2,…, pm); Q=(q1, q2,…, qn). При оптимальной стратегии игрока А выполняется условие, как мы уже выяснили (9.1, 9.2):
 ,
,
а оптимальной стратегии игрока В удовлетворяет условие:
 .
.
Таким образом, можно рассмотреть задачу отыскания оптимальной стратегии игрока А, для которой имеют место следующие ограничения:
|
| (9.3) |
Величина v (цена игры) неизвестна, однако можно преположить, что v>0, если все элементы платежной матрицы неотрицательны, а этого всегда можно достигнуть, как упоминалось, прибавляя ко всем элементам матрицы некоторое положительное число.
Преобразуем систему ограничений, разделив все члены неравенств на v. В результате получим:
|
| (9.4) |
где ti = pi/v, i=1, 2, …, m.
Из условия p1+p2+ … +pm=1 следует, что t1+t2+ … +tm=1/v.
Решение игры должно максимизировать значение v, значит, функция  должна принимать минимальное значение.
должна принимать минимальное значение.
Таким образом, получена задача линейного программирования:  при ограничениях (9.4) и дополнительных условиях неотрицательности переменных ti(i=
при ограничениях (9.4) и дополнительных условиях неотрицательности переменных ti(i= ). Решая её, находим значение ti и величину 1/v, затем отыскиваем значение pi=vti.
). Решая её, находим значение ti и величину 1/v, затем отыскиваем значение pi=vti.
Для определения стратегии игрока В запишем следующие условия:
|
| (9.5) |
Разделив все члены неравенств на v, получим:
| Люди также интересуются этой лекцией: 39 Сопоставление теоретических и экспериментальных данных.
| (9.6) |
где uj=qj/v, j=1, ... , n. Переменные u1, u2, …, un должны быть выбраны так, чтобы выполнялись условия (9.6) и достигался максимум функции
| W=u1+u2+…+un=1/v, uj³0. | (9.7) |
Таким образом, для решения игры имеем пару двойственных симметричных задач линейного программирования. Используя свойство симметричности, можно решить одну из них, требующую меньших вычислений, а решение второй задачи найти на основании оптимального плана двойственной.


 сij
сij .
. .
.