Классификация задач управления запасами

Классификация задач управления запасами

          Задачи управления запасами по наличию того или иного признака можно разделить:

1) По количеству управляемых периодов (пополнения запасов) на однопериодные и многопериодные. Если пополнение запасов производится в системе один раз, такая задача управления запасами называется однопериодной, в противном случае – многопериодной. Так, например, автомашина может один раз заправиться и сделать ещё дополнительный запас горючего или у неё есть возможность подзаправляться во время перевозок.

2) По характеру пополнения запасов с непрерывной системой пополнения запасов (мгновенной) и периодической (с задержкой). Если при уменьшении запаса до определённого уровня происходит его пополнение, то мы имеем задачу с непрерывном пополнением запасов. При этом необходим постоянный контроль за уровнем запаса. Разновидностью такой системы является система “двух бензобаков” (“двух бункеров”, “двух складов”). Один из бензобаков (бункеров, складов) выдает запас (горючее) только в том случае, если кончается запас в другом, одновременно подаётся сигнал о необходимости пополнения бензобаков (бункеров, складов).

3) По учёту характера спроса на детерминированные и вероятностные (стохастические). Если невозможно точно предсказать спрос с момента поступления запаса до момента его пополнения, то имеем вероятностную задачу управления запасами, в противном случае – детерминированную. Так, если неизвестен маршрут движения автомашины (состояние дороги, уклоны, подъёмы, …), то практически невозможно точно предсказать расход горючего.

4) По количеству типов ресурсов на однопродуктовые и многопродуктовые. Если запас включает несколько видов продукции, то имеем многопродуктовую задачу управления запасами, в противном случае – однопродуктовую. Так, если для автомашины кроме бензина будем учитывать расход масла, то это уже будет многопродуктовая задача управления запасами.

5) По виду целевой функции на задачи с пропорциональными и непропорциональными затратами. Если издержки производства на единицу продукции постоянны, и весь объём спроса в конечном счете удовлетворяется, то мы имеем дело с пропорциональными затратами, в противном случае – с непропорциональными. Так, затраты на 1 км пробега автомашины могут быть постоянными, а могут быть переменными (например, зависят от дальности ездки).

Однопродуктовая детерминированная задача управления запасами

Рекомендуемые материалы

Постановка задачи и выбор критерия оптимизации

          Пусть месячная потребность предприятия в какой – либо материале (песок, щебень, цемент,…) составляет  Q  условных единиц. Расход этого материала во времени происходит равномерно. Необходимо определить, каков должен быть размер поставки материала, чтобы суммарные затраты на создание и хранение запаса были минимальны.

Выявление основных особенностей, взаимосвязей и количественных закономерностей

          Обозначим   затраты на хранение единицы запаса в единицу времени, а   затраты на доставку партии материалов. Пусть затраты    не зависят от количества материалов в поставленной партии. Предполагается, что все партии состоят из одинакового числа единиц материала,  величина поставок. Изобразим графически движение запасов в течение времени (месяца)  . Обозначим   промежуток времени (период) от момента поставок партии материала до момента её израсходования. Количество необходимых поставок для удовлетворения месячной потребности в материале:

.

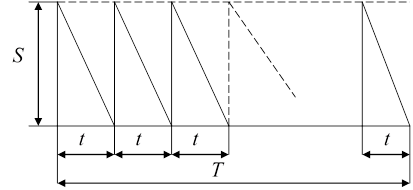Рис. 11.3 Движение запасов с мгновенным временем их пополнения

Построение математической модели

Суммарные месячные расходы на хранение материала и доставку за период  :

.

Исследование математической модели

Продифференцировав целевую функцию относительно  S  и приравняв производную    к нулю, получим

,

откуда

 .

          Это выражение носит название формулы Вильсона (Уилсона), из которой можно установить оптимальный размер поставок. С помощью этой формулы можно определить и оптимальные моменты времени пополнения запасов.

          Теперь усложним задачу, будет учитывать убытки, если спрос не удовлетворён.

Задача управления запасами с учётом убытков

из-за неудовлетворённого спроса

Постановка задачи

Пусть на предприятии вследствие неудовлетворённого спроса возникают убытки, характеризующиеся величиной    на единицу ресурса в единицу времени. В течение времени    каждого периода    уровень запаса достаточен для удовлетворения спроса, а затем в течение интервала    запас отсутствует, причем неудовлетворённый спрос покрывается из следующей партии с момента поступления на склад. Пусть потребность в материале составляет    единиц в период  .

          Определить, какими должны быть поставляемая  S  и потребная  V  партии, чтобы затраты на доставку и хранение с учётом неудовлетворённого спроса были минимальными.

Выявление основных особенностей, взаимосвязей и количественных закономерностей

Обозначения те же, что и ранее. Графически движение запасов при неполном удовлетворении спроса представлено на рис. 11.4.

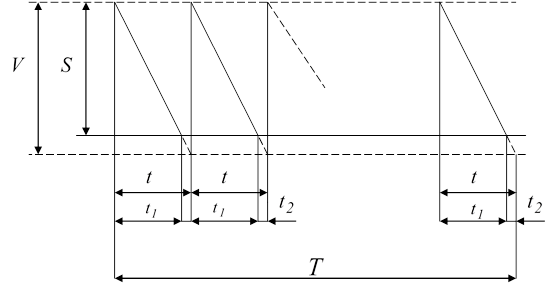Рис. 11.4 Движение запасов с учётом убытков из-за неудовлетворённого спроса

По графику легко составить следующие закономерности:

.

Построение математической модели

Суммарные затраты на хранение, доставку и потери из-за неудовлетворённого спроса за период  T:

.

Исследование математической модели

Чтобы определить минимум функции, находим частные производные от  Y  по  S  и  V  и приравняем их к нулю:

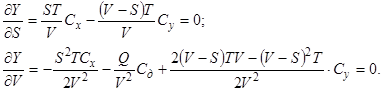
Решив систему уравнений, получим:

   .

Общая детерминированная многопериодная

задача управления запасами

Постановка задачи и выбор критерия оптимизации

          Пусть месячная потребность предприятия в каком – либо материале составляет  Q  условных единиц. Расходуется материал равномерно. При неудовлетворении спроса на предприятии возникают убытки, измеряемые величиной    на единицу материала в единицу времени. Затраты на хранение единицы материала в единицу времени составляют  . Затраты на поставку партии материала - . В течение периодов    происходит поставка материала предприятию. Определить оптимальные размеры поставляемой и потребной партии материала, минимизирующие затраты на доставку и хранение.

Выявление основных особенностей, взаимосвязей и количественных закономерностей

          Представим графически движение запасов при неполном удовлетворении спроса и с задержкой пополнения запасов.

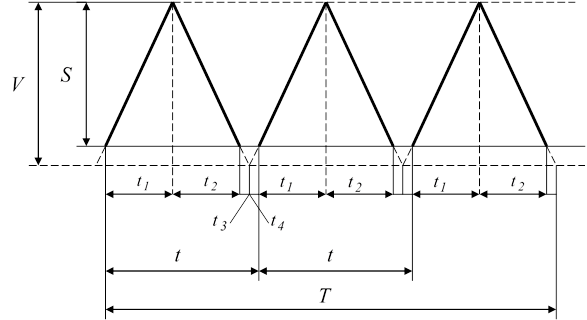Рис. 11.5 Движение запасов с учётом убытков из-за неудовлетворённого спроса и с задержкой их пополнения

          Из графика можно установить следующие соотношения:

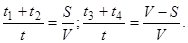
Построение математической модели

Суммарные затраты на хранение, доставку и потери из-за неудовлетворённого спроса за период  T.

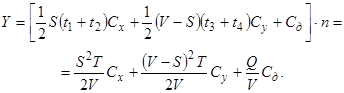
Исследование математической модели

Продифференцировав целевую функцию  Y  относительно  V  и  S  и прировняв полученные при этом частные производные    и    к нулю, получим систему уравнений:

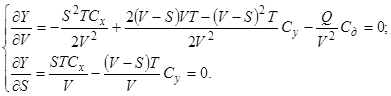
или

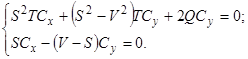
Решив систему уравнений, находим:

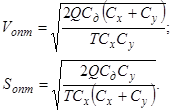
Одновременно с определением оптимальной величины потребной    и поставленной    партий можно определить оптимальный интервал времени между двумя поставками:

Если Вам понравилась эта лекция, то понравится и эта - 11.2 Курс на строительство социализма в одной стране.

.

После соответствующих преобразований получим

.

          Задачу управления запасами при случайном спросе не будем рассматривать.

Задачи замены оборудования

          Технические характеристики любой машины и оборудования вследствие старения, износа и других причин со временем ухудшаются. Это приводит к необходимости замены оборудования с целью как уменьшения суммарных затрат на эксплуатацию оборудования, так и предупреждения его полного выхода из строя (отказа). Кроме того, это приводит к необходимости рационально организовать профилактическое обслуживание.