Теория статистических решений

Тема 9. Теория статистических решений

1. Теория статистических решений

Теория статистических решений - это математическая теория принятия решений в условиях неопределённости в тех слу­чаях, когда характер неопределённости может быть описан вероят­ностной моделью. Часто к теории статистических решений относят лишь динамические модели. Если распределение вероятностей исходных данных пол­ностью известно, теория статистических решений, по существу, смыкается с теорией стоха­стической оптимизации. Специфические и глубокие проблемы воз­никают в ситуациях, когда указанное распределение вероятностей известно не полностью, например, задано с точностью до неизвест­ного параметра, вообще говоря, произвольной природы. Формаль­ная схема восходит к работе американского математика А. Вальда и состоит из следующих элементов.

1. Конечный или бесконечный случайный вектор наблюде­ний Х= (Х,,Х₂,...). (Более строго, X - измеримое отображение, определенное на некотором исходном измеримом пространстве элементарных событий.)

2. Семейство  возможных распределений вероятностей век­тора наблюдений X. Как правило, полагают , где  - неизвестный параметр, вообще говоря, произвольной природы;  - множеству возможных значений параметра.

3. Пространство возможных решений D = {d). Так, если  = {0,1} (неизвестный параметр  = 0 или 1), и задача состоит в различе­нии двух гипотез: ={истинное значение  = 0} и  = {истин­ное значение  = 1}, то естественно положить D = {0, 1}, считая, что решение d = 0 (1) соответствует принятию  ().

4. Решающая функция или статистика , принимаю­щая значения в пространстве решений , т. е. правило соответ­ствия между значением вектора наблюдений и принимаемым ре­шением.

Задача состоит в определении понятия «хорошей» решающей функции и её поиске. Как правило, для этого вводится дополни­тельный элемент схемы:

5) Функция потерь  - потери при решении  и истинном значении неизвестного параметра . Единица измерения потерь и сама функция  определяются спецификой конкретной задачи. Например, в задаче оценивания одномерного параметра , когда решение d суть оценка , часто полагают  (квад­ратичные потери). Могут быть задачи, где вместо потерь рассмат­ривается «доход», возможны обобщения понятия потерь - вектор потерь и т. п.

Рекомендуемые материалы

Если принимаемое решение , то потери суть случай­ная величина , и нужно выбрать решающую функцию Т, порождающую наиболее «устраивающее» распределение вероят­ностей случайной величины . Иначе, мы должны устано­вить отношение предпочтения на множестве возможных распре­делений указанной случайной величины. Наиболее распростра­нённый путь - минимизировать средние потери , где  - операция вычисления математического ожидания в случае, когда неизвестный параметр равен . На­пример, при различении двух гипотез, как правило, считают , если , и , если . В этом случае , то есть вероятности принять неверное реше­ние. Называемая функцией риска или просто риском характери­стика суть функция по отношению к  и функционал по отношению к решающей функции .

Особенностью теории статистических решений является тот факт, что непосредствен­ная минимизация  по Т бессмысленна, так как в нетривиаль­ных случаях минимум достигается на решающей функции, зави­сящей от параметра , который неизвестен. Рассмотрим несколь­ко вариантов преодоления указанной принципиальной трудности.

Первый состоит в уточнении и обогащении самого принципа оптимальности. Говорят, что решающая функция ( «луч­ше» ), если  для всех , и хотя бы в одном случае неравенство строго. Решающая функция Парето - оптимальна или допустима, если не существует решающей функции лучше её. Ясно, что класс рассматриваемых решающих функций можно сузить до класса Парето - оптимальных решающих функ­ций, но, как правило, последний ещё достаточно широк. Выбор из этого класса одного представителя должен определяться до­полнительными соображениями.

Один из наиболее распространённых подходов основан на прин­ципе минимакса и состоит в минимизации максимального по от­ношению к  риска, точнее, к минимизации . Минимаксный подход правомерен при «равной значимости» потерь при разных значениях неизвестного параметра. В иных случаях нуж­ны другие подходы. Так, если  = {0, 1}, часто экзогенно вводит­ся значение максимально допустимых потерь  при , т. е. вводится условие , и уже при этом условии минимизи­руется  (подход Неймана —Пирсона). В такой постановке к потерям при  = 0 «отношение более осторожное», чем при =1. Возможны и иные подходы, например, минимизация функциона­ла , где  - суть веса, и т. п.

Второй путь сводится к сужению класса рассматриваемых решающих функций, т. е. к рассмотрению лишь тех из них, ко­торые обладают дополнительными «естественными» свойства­ми, определяемыми спецификой конкретной задачи. Например, если в задаче оценивания  - параметр сдвига, то есть наблюде­ния , где случайные величины  имеют одно и то же распределение, не зависящее от , естественно использовать принцип эквивариантности, предписывающий рассматривать лишь те решающие функции , для которых

.

Если , минимизация риска уже осмыслена, так как минимум достигается на решающей функ­ции, не зависящей от . То же верно, если  — параметр масшта­ба, то есть , и рассматриваются решающие функции , для которых .

Третий путь основан на Байесовском подходе к оцениванию, возможном, когда параметр  является случайной величиной с заданным (априорным) распределением вероятностей. В этом случае  есть случайная величина, средние потери равны , где математическое ожидание М вычисляется «относительно случайной величины », и правомерна задача минимизации . С математической точки зрения байесовский подход безупречен, но на практике ситуации, когда априорное распределение существует и известно, редки.

Недостатком всех перечисленных подходов является то, что они привязаны к функции потерь, выбор которой часто, в той или иной мере, субъективен. Поэтому в ряде ситуаций более естествен­ны методы, вообще не аппелирующие к понятию потери. Примером может служить предложенный Д. Фишером метод максимального прав­доподобия, используемый в задачах оценивания неизвест­ного параметра . Пусть распределение  имеет плотность веро­ятностей  относительно некоторой универсальной (не зави­сящей от ) меры . Обсуждаемый метод основан на том сообра­жении, что значение вектора наблюдений, как правило, попадает в «зону наиболее вероятных значений», т. е. в область, где плот­ность вероятностей «велика». Соответственно, во многих отно­шениях естественной оказывается оценка максимального правдо­подобия

.

Дальнейшее обобщение схемы связано с идеей рандомизации, когда при уже заданном значении вектора наблюдений X реше­ние принимается не однозначно, как выше, а с помощью некото­рого случайного механизма, зависящего от X. Точнее, вектору наблюдений X ставится в соответствие не решение , а зави­сящее от X и определённое на D распределение вероятностей . При этом решение  принимается таким образом, чтобы вероятность того, что при уже наблюдённом  решение , равнялась . Если распределение  вырождено в некото­рой точке , схема сводится к предыдущей. В случае рандо­мизации (случайные) потери равны , где математическое ожидание берётся «относительно случайной ве­личины d, имеющей распределение вероятностей ». Риск в этом случае равен . Рандомизация не ис­ключает применения всех вышеупомянутых подходов. Следует отметить, что при некоторых не слишком обременительных ус­ловиях типа выпуклости и гладкости исходных распределений рандомизация не приводит к фактическому уменьшению риска.

Динамические модели укладываются в построенную схему и обладают следующей спецификой. Компонента  вектора на­блюдений  интерпретируется как наблюдение в момент времени t=l,...,n, где или  (конечное время наблю­дений), или  (время наблюдений бесконечно). Каждому t соответствует своё пространство решений . Решение в момент t определяется функцией , принимающей значения в . (В рамках предыдущей схемы сказанному соответствуют соотноше­ния  и ).) При этом предполагается, что  т. е. решение принимается лишь на основе уже наблюдённых значений вектора наблюдений. Типичным при­мером функции потерь в динамической ситуации может служить функция — , где  интерпретируется как поте­ри в момент  при наблюдении  и решении , а всё выраже­ние - как средние потери на единицу времени при общем време­ни . (Если , можно рассматривать, скажем, верхний пре­дел последнего выражения.) Динамическая схема принятия ре­шений наследует все перечисленные выше подходы.

Одной из наиболее ярких идей, используемых при исследова­нии динамических моделей, является также восходящая к А. Вальду идея последовательного статистического анализа, состоящая в предложении отказаться от априорной фиксации числа наблюде­ний и в каждый момент времени, на основе наблюдённых значе­ний компонент вектора наблюдений, решать вопрос: продолжать наблюдения или нет. В указанной постановке каждое из про­странств  содержит специфическое решение «продолжить на­блюдения», а все остальные решения носят характер «оконча­тельных» - при их принятии наблюдения заканчиваются. В этом случае число наблюдений будет уже случайной величиной, струк­тура которой определяется выбранной последовательностью ре­шающей функции .

Оказывается, что при прочих равных условиях применение последовательного анализа позволяет уменьшить средние потери или среднее время наблюдений. Одним из наиболее показатель­ных в этом отношении примеров может служить последовательный критерий отношения вероятностей при различении двух ги­потез - применение последовательного анализа приводит в этой задаче к существенному снижению требуемого объёма выборки при тех же вероятностях ошибок в принятии решений.

2. Имитационное моделирование и метод статистических испытаний

Экономико-математическая (преимущественно компьютерная) имитационная модель позволяет проводить исследования кото­рой проводится экспериментальными методами. Термин введён в начале 1960-х годов, его границы довольно широки и не слишком чётко определены.

Появление имитационного моделирования связано с «новой волной» в экономико-ма­тематическом моделировании. Проблемы экономической нау­ки и практики в сфере управления и экономического образова­ния, с одной стороны, и рост производительности компьютеров, с другой, вызвали стремление расширить рамки «классических» экономико-математических методов. Наступило некоторое ра­зочарование в возможностях нормативных, балансовых, опти­мизационных и теоретико-игровых моделей, поначалу заслу­женно привлёкших к себе тем, что они вносят во многие проб­лемы управления экономикой обстановку логической ясности и объективности и непосредственно приводят к «разумному» (сбалансированному, оптимальному, компромиссному и т.п.) решению. Выявился широкий класс проблем, в которых эти модели не улавливают существенных явлений реальности. Не всегда удаётся полностью осмыслить априорные цели и, тем более, формализовать критерий оптимальности и (или) огра­ничения на допустимые решения. Поэтому многие попытки всё же применить такие методы стали приводить к получению неприемлемых, например, нереализуемых (хотя и оптималь­ных) решений. Преодоление возникших трудностей пошло по пути отказа от полной формализации (как это делается в нор­мативных моделях) процедур принятия социально-экономиче­ских решений. Предпочтение стало отдаваться разумному синтезу интеллектуальных возможностей эксперта и информаци­онной мощи компьютера (см. Диалоговая система). Одно течение в этом направлении — переход к «полунормативным» многокритериальным человеко-машинным моделям; второе — перенос центра тяжести с прескриптивных моделей, ориентиро­ванных на схему «условия — решение», на дескриптивные моде­ли, дающие ответ на вопрос, «что будет, если...?» (см. Система поддержки принятия решений).

Первый признак имитационного моделирования — ориентированность на такую схе­му. В ходе экспериментов с имитационными моделями эксперты задают ей вопросы, модель доставляет ответы; эксперты их анализируют и форми­руют знания, суждения, решения. Вторая особенность имитационного моделирования — более подробное, чем в классических моделях, отображение структуры прототипа в структуру модели, использующее бога­тые и гибкие возможности современных средств организации и обработки данных. В этом — отличие современных имитационных моделей от дескриптивных эконометрических моделей, хотя последние можно рассматривать как частный случай имитационных моделей. Эконометрическая модель устроена как чёрный ящик и не отображает внутренних связей в прототипе. Её параметры оцениваются в результате статистической обработки наблюдений за действительностью. Может оказаться, что эти оценки верны только в условиях действующего экономического механизма, и для анализа явлений, которые могут возникнуть в условиях проектируемого эконо­мического механизма, более или менее существенно отличаю­щегося от действующего, модель становится непригодной. Но изучение свойств экономических механизмов, радикально от­личных от прежних, особенно актуально. Если конструктор модели вынужден по такой причине отказаться от моделирова­ния «в лоб», он пытается понять и отобразить внутренние при­чинно-следственные связи и механизмы и для этого предста­вить модель в виде совокупности «атомов» — компонентов, для каждого из которых он способен построить правдоподоб­ную модель и все существенные отношения между которыми он способен правдоподобно отобразить. Такой способ приво­дит к правдоподобной модели — особенно, если в качестве компонентов модели выбирать модели компонентов системы-прототипа (предприятия, цеха, банки, регионы, транспортные сети, органы управления, группы населения и т. п.). Усложне­ние структуры имитационной модели вызывается также стремлением использо­вать её в качестве средства проверки доброкачественности ре­шений, формируемых экспертом или нормативной (т. е. более простой) моделью. Для моделирования первичных структурных единиц («атомов») иногда удаётся привлекать и классические подходы. Так, для отображения технологических процессов уместно использовать эконометрические промышленные и сельскохозяйственные производственные функции, явно не за­висящие от механизма управления производством. Для постро­ения функций спроса могут быть использованы оптимизацион­ные модели, так как здесь критерий оптимальности и ограниче­ния можно иногда формулировать обоснованно. Третья особенность имитационной модели состоит в том, что это, как правило, не «кар­тинка» как, скажем, статическая модель межотраслевого ба­ланса, в которой разновременные события «склеены» в одномо­ментные, а скорее, «фильм», отображающий функционирова­ние прототипа в виде смен состояний модели в последовательные моменты и — в этой связи — появление разных способов моде­лирования времени. Эта особенность родилась из отмеченной выше потребности не только получить подходящие решения (роль нормативной модели на этом завершается), но и вклю­чить в модель компоненты, отображающие отклик системы на принятые решения — в виде показателей её функционирова­ния. Классическую динамическую балансовую модель и её раз­новидности можно рассматривать как частный, «вырожден­ный» случай имитационной модели. Хотя функционирование и моделируется, но моменты производства, распределения и потребления ре­сурсов сводятся в один. В результате чего модель слишком жёстко описывает важные явления, связанные с разными рит­мами производств поставщиков и потребителей, последствия срывов договоров поставки. В «невырожденных» имитационных моделях получает отражение то обстоятельство, что процессу потребления ресурсов предшествуют процессы производства и распределения. Четвёртая особенность имитационной модели — свободный вы­бор средств для моделирования процессов (в то время как классические модели используют сравнительно узкий круг ма­тематических конструкций: линейные уравнения и неравенства, оптимизация линейных или дробно-линейных функций, регрес­сионный анализ, методы теории массового обслуживания). Мо­дели процессов — это машинные и человеко-машинные алго­ритмы. Они:

· вычисляют значения модельного времени;

· изменя­ют значения переменных, представляющих состояния компонентов модели;

· генерируют по ходу моделирования но­вые компоненты (например, сдаваемые в эксплуатацию строя­щиеся промышленные предприятия или выставляемые платёжные требования);

· уничтожают компоненты (разорив­шиеся предприятия или оплаченные платёжки).

В алгоритмы моделирования процессов включаются иногда и процедуры, генерирующие случайные значения некоторых переменных (представляющих, например, текущие погодные условия или отклонение объёмов поставки от договорных). Пятая особен­ность — широкие возможности диалога экспериментатора с моделью в ходе её выполнения, в то время как с выполняемой на компьютере классической моделью экспериментатор кон­тактирует лишь перед её запуском (задавая значения её изме­няемых параметров) и после её завершения (интерпретируя по­лученные результаты).

Перечисленные особенности не исчерпывают, возможно, всех свойств моделей, которые разные авторы склонны назы­вать имитационными; с другой стороны, некоторые авторы на­зывают имитационными модели, обладающие лишь частью этих свойств; наконец, некоторыми из перечисленных свойств могут в той или иной степени обладать и классические модели, особенно их модификации.

Для представления структур и процессов имитационного моделирования используют­ся универсальные и специализированные языки программиро­вания, проблемно-ориентированные пакеты прикладных про­грамм, различные универсальные и специализированные сис­темы управления базами данных. Все эти средства позволяют моделировать разнообразные структуры и различные отноше­ния между их компонентами: подчинённость, собственность, договорённость и т. п. Моделирование процессов может наталкиваться на методологические трудности. В первую очередь это относится к моделированию человеческого поведения, в ча­стности процессов принятия решений. Это одна из причин, по которой модели процессов реализуются иногда в виде челове­ко-машинных алгоритмов: некоторые элементы человеческого поведения моделируются специально привлечёнными людьми. Такое участие людей в эксперименте с имитационными моделями приобретает ино­гда форму имитационной управленческой игры. Точность ото­бражения прототипа определяется структурой модели, свойст­вами алгоритмов, моделирующих процессы, и реальностью числовой информации, используемой в модели. Сложность имитационных моделей и их прототипов, сложность проведения и интерпретации экспериментов с ними приводит к тому, что в данной сфере за­труднительно, а иногда и принципиально невозможно приме­нить формализованные (например, статистические) методы оценки адекватности модели, используемые в естественных на­уках и технике. Здесь зачастую приходится оперировать субъ­ективными понятиями, принятыми в гуманитарных областях: доверие к модели, правдоподобие модели, убеждённость в её применимости и т. п. Имитационные модели являются подходящим инструмен­том для системных исследований.

Получение решений в имитационном моделировании производится с помощью метода статистических испытаний. Это численный ме­тод решения математических задач, основанный на моделирова­нии случайных величин или процессов и последующем построе­нии статистических оценок для искомых величин. Другое назва­ние метода статистических испытаний - метод Монте-Карло - в большей степени отно­сится к модификациям метода статистических испытаний. Универсальность метода статистических испытаний как ме­тода вычислительной математики определяется возможностью его использования для решения задач, не связанных со случайнос­тью. Это достигается построением вспомогательных вероятност­ных моделей, куда в качестве параметров входят подлежащие определению постоянные величины.

Простейшая схема метод статистических испытаний такова. Для определения неизвест­ной величины  подыскивается случайная величина , математи­ческое ожидание которой равно . Если  независимы и одинаково распределены так же, как , то при достаточно боль­шом  по закону больших чисел средняя арифметическая этих величин  будет приближённо равна :

 при  и .

Этот факт указывает способ расчёта а путём моделирования случайной величины . С помощью центральной предельной теоремы можно получить оценку погрешности. Эта погрешность стремится к нулю с ростом  и, например, с большой вероятно­стью не превосходит , где . Таким образом, например, представляют многомерный интеграл в виде математического ожидания функционала от случайного процесса, который затем моделируется. Известны вероятностные модели для вычисле­ния интегралов, для решения интегральных уравнений систем линейных алгебраических уравнений, краевых задач для эллип­тических уравнений, для оценки собственных значений линей­ных операторов и т. д.

Моделирование случайных величин с заданными распределе­ниями, как правило, осуществляется путём преобразования од­ного или нескольких независимых значений случайной величи­ны а, распределённой равномерно в интервале (0, 1). Последо­вательности «выборочных» значений  обычно получают на ком­пьютере с помощью теоретико-числовых алгоритмов; такие чис­ла называются псевдослучайными.

Если в расчёте по методу статистических испытаний моделируются случайные величи­ны, определяемые конкретным содержанием изучаемого явле­ния, то такой расчёт часто бывает неэффективным. Эта неэф­фективность обычно проявляется в слишком большой величине погрешности (дисперсии) оценок искомых величин. Разработа­но много способов уменьшения дисперсии указанных оценок в рамках метода статистических испытаний. В частности, можно выбрать более подходящую вероятностную модель.

Как было отмечено, метод Монте-Карло это численный метод, использующий моделирование слу­чайных величин и построение статистических оценок для иско­мых величин. Первоначально алгоритмы метода Монте-Карло применялись для:

· оценки многократных интегралов;

· решения интегральных уравнений 2-го рода.

Алгоритм для оценки многократных интегралов.

Пусть необходимо оценить интеграл  по мере Лебега в евклидовом -мерном пространстве и  — плотность ве­роятности такая, что  можно записать в виде математического ожидания следующим образом:

,

где . Моделируя  на компьютере, можно полу­чить  выборочных значений . Согласно закону больших чисел,

.

Одновременно можно оценить среднеквадратическую по­грешность , т.е. величину , и приближённо построить подходящий доверительный интервал для . Выбором плотности  можно распорядиться для получения оценки с возможно меньшей дисперсией. Соответствующие алгоритмы называются существенной выборкой (выборкой по важности). Иногда полезны сочетания метода Монте-Карло с классическими квадра­турами — т. н. случайные квадратурные формулы, основная идея которых состоит в том, что узлы и коэффициенты ка­кой-либо квадратурной суммы (например, интерполяционной) выбираются случайно из распределения, обеспечивающего несмещённость получаемой оценки интеграла. При этом порядок скорости сходимости метода Монте-Карло повышается и в некоторых слу­чаях становится максимально возможным на рассматриваемом классе задач.

Если подинтегральная функция зависит от параметра, то це­лесообразно использовать метод зависимых испытаний, т. е. вычислять интегралы для различных значений параметра по одним и тем же случайным узлам. Важным свойством метода Монте-Карло является сравнительно слабая зависимость среднеквадратич­ной погрешности  от размерности задачи, причём порядок сходимости по числу узлов  всегда один и тот же: . Это позволяет вычислять (после предварительных преобразова­ний задачи) интегралы очень высокой и даже бесконечной кратности.

Алгоритмы метода Монте-Карло для решения интегральных уравнений 2-го рода

Пусть необходимо вычислить линейный функцио­нал , где , причём для интегрального опера­тора  с ядром  выполняется условие, обеспечивающее сходимость ряда Неймана: . Цепь Маркова  опреде­ляется начальной плотностью  и переходной плотностью ; вероятность обрыва цепи в точке  равна

;

 — случайный номер последнего состояния. Далее определя­ется функционал от траектории цепи, математическое ожидание которого равно . Чаще всего используется т. н. оценка по столкновениям

,

где

, .

Если  при  и  при , то при некотором дополнительном условии

.

Возможность достижения малой дисперсии в знакопостоянном случае показывает следующее утверждение:

если  и ,

где , то , .

Моделируя подходящую цепь Маркова на компьютере, получают статистическую оценку линейных функционалов от решения интегрального уравнения 2-го рода. Это даёт возможность и локальной оценки решения на основе представления: , где . В методе Монте-Карло оценка пер­вого собственного значения интегрального оператора осущест­вляется итерационным методом на основе соотношения

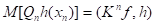
Все рассмотренные результаты почти автоматически распро­страняются на системы линейных алгебраических уравнений вида .

Решение дифференциальных уравнений осуществляется методом Монте-Карло на базе соответствующих интегральных соотноше­ний. Изложенное представляет собой основу для построения эффективных модификаций статистического моделирова­ния.

Литература

Бесплатная лекция: "3 Гражданские правоотношения" также доступна.

1. Типология потребления, под ред. С.А. Айвазяна и Н.М. Римашевской, М., 1978.

2. Айвазян С.А., Бухштабер В.М., Енюков И.С, Мешалкин Л.Д., Прикладная статистика: классифика­ция и снижение размерности, М., 1989.

3. Методы анализа данных: подход, основанный на методе ди­намических сгущений, пер. с франц., М., 1985

4. Жамбю М., Иерархи­ческий кластер-анализ и соответствия, пер. с франц., М., 1988.

5. Айва­зян С.А., Бухштабер В.М., Епюков И.С, Мешалкин Л.Д., Прикладная статистика: классификация и снижение размерности, М., 1989

6. Tryon R.C., Cluster Analysis, Ann. Arb., Edw. Brothers, 1939.