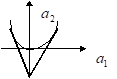Фильтры второго и высших порядков

Лекция 7.  Фильтры второго и высших порядков

Определение фильтра второго порядка

Примером фильтра вторго порядка является фильтр . Рассматриваем только вещественный случай. Переходя к Z- преобразованию, получим: . Найдя корни многочлена в знаменателе, перепишем

. Это означает, что фильтр есть последовательное соединение двух фильтров первого порядка. Для устойчивости достаточно потребовать, чтобы все корни были по модулю меньше единицы. Это означает, что . Рассмотрим вещественный случай: . Это область под параболой. Условие на модуль первого корня имеет вид . Возводя второе неравенство в квадрат, получим . Для выполнения первого  из неравенств достаточно чтобы . Аналогичное рассмотрение условия на второй корень дает . Окончательно, область имеет форму. Для  комплексных корней . Кроме того, квадрат модуля корня равен , откуда вытекает, что . 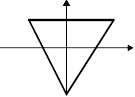Объединяя обе области, получаем треугольник устойчивости.

 Другими словами, если точка с координатами  попадает внутрь треугольника, соответствующий фильтр будет устойчивым.

Фильтры высших порядков

Функции управления и структура туристско-экскурсионной организации - лекция, которая пользуется популярностью у тех, кто читал эту лекцию.

Предположим, что передаточная функция фильтра имеет вид

, где в числителе и знаменателе стоят вещественные многочлены, причем  имеет степень выше двух. В этом случае имеет место разложение  на неприводимые многочлены первой и второй степеней с вещественными коэффициентами, а сам фильтр можно заменить последовательным соединением  фильтров. Если  и сомножители взаимно простые, то для некоторых многочленов . Отсюда следует, что . Другими словами, фильтр можно представить как праллельное соединение двух фильтров. Построив базисные фильтры второго и первого порядка, можно с их помощью реализовать фильтр любого порядка.

Фильтр Баттеруорта (Butterworth)

Это один из базисных фильтров. Фильтр низких частот имеет передаточную функцию

,  (1)

Это фильтр порядка М . В зависимости от значений  меняются характеристики фильтра. Задача заключается в отыскании вещественных коэффициентов фильтра по заданным параметрам. Будем искать фильтр в виде

. Передаточная функция имеет вид . Положим . Тогда  и Должно быть выполнено равенство . Слева и справа находятся аналитические функции от z. Если они совпадают на какой-либо линии, они равны всюду, где имеют смысл.