Дискретное преобразование Фурье

Лекция 4. Дискретное преобразование Фурье (ДПФ)

В данной лекции установим свойства дискретного преобразования Фурье аналогичные свойствам непрерывного преобразования. Как обычно, преобразования типа почленного интегрирования ряда, перестановки порядка суммирования и т.п будут проводится без какого-либо обоснования. Предполагается, что соответствующие функции обладают необходимыми свойствами.

Основное определение: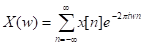

Формула  обращения

Как уже отмечалось, ДПФ является периодической функцией. В дальнейшем при изложении свойств ДПФ будем предполагать, что  . В этом случае период ДПФ равен 1. Обратное преобразование получается почленным интегрированием ряда. Если , то обратное преобразование задается формулой . Данная формула вытекает из соотношения: интеграл  равен 0 при  и 1 иначе.

Свертка

Свертка двух последовательностей определяется  формулой: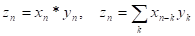

Предложение. ДПФ от свертки двух последовательностей равняется произведению из преобразований Фурье,  а ДПФ от произведения двух последовательностей есть свертка их преобразований Фурье.

Доказательство. Найдем преобразование от произведения последовательностей. Имеем =  =.

В силу периодичности подынтегральных функций, получим .

Найдем ДПФ от свертки. По определению , . Перемножая эти ряды и собирая коэффициенты при одинаковых степенях, получим  

Отметим очевидные следствия вещественности исходной последовательности: .

Пример вычисления ДПФ

Рекомендуемые материалы

Ранее было подсчитано ДПФ от единичной последовательности. В реальных условиях полагают, что в отрицательные моменты времени сигнал отсутствует. В этой связи интересно найти ДПФ от дискретного аналога функции .

Предложение.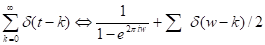

Доказательство. Положим =. Теперь

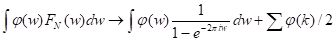
Задача 3. Доказать, что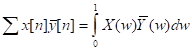

Линейные инвариантные системы.

Рассматриваются последовательности . Очевидным образом определяются сумма последовательностей и произведение на число. В результате  сдвига получается новая последовательность . Дальнейшее работа с последовательностью, полученной в результате дискретизации, заключается в преобразовании с помощью  различных устройств.

Система  осуществляет это преобразование: .. отметим, что  выходная последовательность  является функцией от всей входной последовательности, то есть каждый член входной последовательности зависит, вообще говоря, от всех членов входной последовательности.

Определение. Система   называется инвариантной, если  для любого .

Рекомендация для Вас - Тема 5. ВЗАИМОДЕЙСТВИЕ ЧЕЛОВЕКА СО СРЕДОЙ ОБИТАНИЯ.

Примеры.

1. Точечные системы: , где  произвольная функция ,- инвариантная система..

2.  для произвольного фиксированного  - инвариантная система

3.  не будет инвариантной. Действительно, пусть . Согласно определению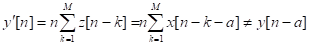

Определение. Система называется линейной инвариантной (ЛИС), если она линейна и инвариантна.

Преобразование в примере 2 осуществляется ЛИС.