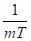Автокорреляция и ее вычисление
Лекция 16. Автокорреляция и ее вычисление
|
|
Пусть задана бесконечная последовательность  . По ней строится автокорреляционная функция
. По ней строится автокорреляционная функция  . Эта функция играет огромное значение в при обработке сигналов. Основное назначение - отыскание максимумов функции
. Эта функция играет огромное значение в при обработке сигналов. Основное назначение - отыскание максимумов функции  , которые интерпретируются как аналоги периодов. Из неравенства Коши следует, что
, которые интерпретируются как аналоги периодов. Из неравенства Коши следует, что  . В точках максимума
. В точках максимума  сдвинутая на
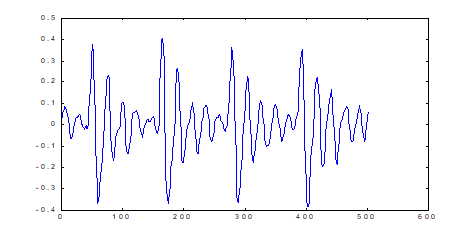
сдвинутая на  исходная последовательность "похожа" на исходную. В качестве примера рассмотрим фрагмент звукового файла с записью звука "а". Этот сигнал не является периодическим в математическом смысле слова, однако, визуально такая периодичность просматривается. Значения периода находятся по максимумам соответствующей автокорреляционной функции. Найдем преобразование Фурье от
исходная последовательность "похожа" на исходную. В качестве примера рассмотрим фрагмент звукового файла с записью звука "а". Этот сигнал не является периодическим в математическом смысле слова, однако, визуально такая периодичность просматривается. Значения периода находятся по максимумам соответствующей автокорреляционной функции. Найдем преобразование Фурье от  . Для непрерывного случая эта задача рассматривалась выше. Положим
. Для непрерывного случая эта задача рассматривалась выше. Положим  . Теперь
. Теперь  , где
, где  - свертка последовательностей.
- свертка последовательностей.  =
=  . С другой стороны,
. С другой стороны,  =
= . Это означает, что
. Это означает, что  . Если исходная последовательность вещественная, то
. Если исходная последовательность вещественная, то  и
и
 (1)
(1)
Случай конечной последовательности
При практическом использовании автокорреляционной функции мы имеем дело с конечными последовательностями. Пусть дана последовательность  . Определим функцию
. Определим функцию  ( как обычно, последовательность считается периодической). Повторяя предыдущие рассуждения, получим для конечного преобразования Фурье в вещественном случае аналог (1)
( как обычно, последовательность считается периодической). Повторяя предыдущие рассуждения, получим для конечного преобразования Фурье в вещественном случае аналог (1)
Информация в лекции "5 Общие правила ИП" поможет Вам.
 (2)
(2)
Если для заданного  существует схема БПФ, то выгоднее для отыскания значений
существует схема БПФ, то выгоднее для отыскания значений  сначала найти преобразование Фурье от исходной последовательности, а затем воспользоваться (2) для отыскания значений функции.
сначала найти преобразование Фурье от исходной последовательности, а затем воспользоваться (2) для отыскания значений функции.
В случае конечных последовательностей мы имеем дело с циклической сверткой. Для того, чтобы избавиться от эффекта цикличности, используется следующий прием. Вместо исходной последовательности длины  берется последовательность
берется последовательность  длины
длины  . Если используются значения
. Если используются значения  , то при их вычислении эффект цикличности не имеет места.
, то при их вычислении эффект цикличности не имеет места.
Практическое оценивание частот
В предыдущий рассмотрениях не учитывалась частота выборки  из исходного непрерывного сигнала. Имеем
из исходного непрерывного сигнала. Имеем
 . Рассматривая последнее выражение как приближение соответствующего интеграла, получим, что данный коэффициент соответствует частоте
. Рассматривая последнее выражение как приближение соответствующего интеграла, получим, что данный коэффициент соответствует частоте  . При выборе значения
. При выборе значения  следует учитывать следующее обстоятельство - увеличение
следует учитывать следующее обстоятельство - увеличение  повышает разрешающую способность, но при этом происходит усреднение по длине окна.
повышает разрешающую способность, но при этом происходит усреднение по длине окна.
Если для оценки периода использована автокорреляционная функция, то максимуму этой функции в точке  отвечает частота
отвечает частота