WaveLet- преобразования

Лекция 11. WaveLet- преобразования

WaveLet-преобразование является альтернативой преобразованию Фурье в тех случаях, когда сигнал не носит периодического характера. Различают непрерывное и дискретное WaveLet-преобразования. Предполагается, что все интегралы, рассмотренные ниже, существуют

Непрерывное преобразование.

Пусть имеется функция  и некоторая функция  - материнская функция. Рассмотрим числа вида

   (1)

Если , то в результате получаем обычное преобразование Фурье ( параметр  не используется по понятной причине). Формула (1) определяет общее Wavelet преобразование. Существует формула обратного преобразования, позволяющая в некоторых случаях восстановить исходную функцию по ее преобразованию. Однако основной смысл преобразования (1) заключается в другом. Величина  не зависит от параметров. Это означает, что вектор, заданный функцией , имеет постоянную длину в смысле пространства  . Предположим, что удалось найти такие значения параметров, для которых   достигает локального максимума. Это означает, что проекция функции  на соответствующую функцию  имеет максимальное значение, поэтому графики этих функций аналогичны. Положив , получим невязку, для которой решается такая же задача. В результате получаем приближение исходной функции функциями, порожденными с помощью функций . Это дает альтернативное описание исходной функции. В зависимости от того, какого рода особенности требуется обнаружить, выбирают вид материнской функции. При цифровой обработке, когда исходная функция задана лишь в отдельных точках, используется дискретное преобразование. Оказалось, что и в общем случае удается построить теорию, напоминающую теорию преобразования Фурье.

На практике, в качестве материнской фуекции при указанном подходе часто используют функцию  ( мексиканская шляпа). Константу  определяют из условия нормировки

Шкалирование

Рассмотрим множество функций  на вещественной оси. Пусть , причем функции  образуют ортонормированную систему. Это означает, что

  (2)

Такую функцию назовем шкалирующей. Например, любая функция, имеющая носитель внутри единичного интервала и норму равную 1, удовлетворяет условию (2). Обозначим через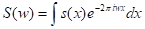

Люди также интересуются этой лекцией: 25 Условное суждение, его строение и условия истинности.

Предложение. Имеет место формула

          (3).

Обратно, из (3) следует (2)

Доказательство.  Имеем  . Поскольку преобразование Фурье является ортогональным преобразованием, . С учетом (2) это означает, что . Далее, пусть . Преобразование Фурье этой функции есть . Теперь , так как остальные слагаемы равны нулю в силу (2). Заменим сумму интегралом и продолжим равенство . Заменим преобразование Фурье от произведения сверткой их образов. Преобразование от первого сомножителя есть он сам. Таким образом, равенство продолжается . Обратное утверждение доказывается переписыванием формул в обратном порядке.

Важным примером материнской функции является функция, равная 1 на интервале  и 0 в остальных точках. Такую функцию обозначим через .

Задача. Найти явный вид формулы (2) для функции .