Теорема об ограничивающей функции

Теорема об ограничивающей функции

Пара (i, j), где i, j – выражение содержащее переменные, используемые в цикле.

Если выполняется:

1) (i, j) – на каждом шаге уменьшается.

                              2).  min iimax i;

                              min jjmax j;

где min i,  max i, min j, max j – некоторые const.

Если 1), 2) – выполняются, то выполнение цикла должно завершиться.

Рекомендуемые материалы

Ограничивающая функция t будет иметь вид:

t: (i - min i)*(1+max j – min j)+j – min j

Пример: сумма элементов двумерного массива

b[0: n-1][0:m-1]

m – строка

n – столбец

{0<m0<n}

i, j:=n-1, m-1

do

            j0 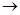 S,j := S+b[i][j] , j-1

        ›  i0  j=0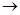 S, i, j :=S+s[i][j], i-1,m-1

od

1) выход из цикла, когда i и j =0 одновременно

0 in

0 jm

2)

{P  B}<i₀,j₀> := <i,j>; S₂{<i₀,j₀> > <i,j>}

wp(“i₀,j₀:=i,j; i,j:=i-1,m-1”, <i₀,j₀> > <i,j>) =

= wp(“i₀,j₀:=i,j; <i₀,j₀> > <i-1,m-1>)=

=<i,j> > <i-1,m-1> = T

Подставим для получения t:

t: (i-0)*(m)+j –0 = i*m+j;

Задача: поезда на станции

Можно выводить поезд, содержащий 1 вагон.

0 число вагонов начальное число вагонов

начальное число вагонов  число поездов 0

Чем больше поездов, тем ближе мы к окончанию работы.

do

            сортировочная непустая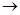

Рекомендуем посмотреть лекцию "16. Экологические аспекты методов разработки".

            выбираем поезд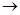

if

                        в поезде 1 вагон  удалить поезд

                    › в поезде больше 1го вагона разбить поезд на две части

fi

od