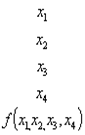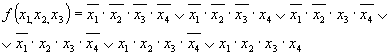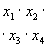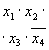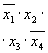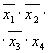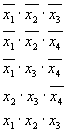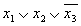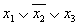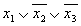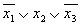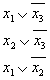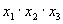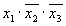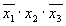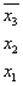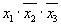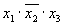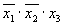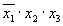Синтез комбинационных устройств
СИНТЕЗ КОМБИНАЦИОННЫХ УСТРОЙСТВ
Канонические формы представления логических функций.
Синтез логического устройства распадается на несколько этапов. На первом этапе требуется функцию, заданную в словесной, табличной или другой формах, представить в виде логического выражения с использованием некоторого базиса. Следующие этапы сводятся к получению минимальных форм функций, обеспечивающих при синтезе наименьшее количество электронного оборудования и рациональное построение функциональной схемы устройства. Для начального представления функции обычно используется базис И, ИЛИ, НЕ независимо от того, какой базис будет использоваться для построения логического устройства.
Исходными, из соображений удобства последующих преобразований, приняты следующие две канонические формы представления функций: совершенная дизъюнктивная нормальная форма (СДНФ) и совершенная конъюнктивная нормальная форма (СКНФ).
Совершенная дизъюнктивная нормальная форма (СДНФ).
Дизъюнктивной нормальной формой (ДНФ) называется такая форма представления функции, при которой логическое выражение функции строится в виде дизъюнкции ряда членов, каждый из которых является простой конъюнкцией аргументов или их инверсий.
Примером ДНФ может служить выражение
|
| (3.9) |
Рекомендуемые материалы
Приведем форму представления функций, не являющейся ДНФ. Например, функция

представлена не в ДНФ, так как последний член не является простой конъюнкцией аргументов.
Также не является ДНФ следующая форма представления функции:

Если в каждом члене ДНФ представлены все аргументы (или их инверсии) функции, то такая форма носит название совершенной дизъюнктивной нормальной формы (СДНФ). Выражение (3.9) не является СДНФ, так как в нем лишь третий член содержит все аргументы функции.


Для перехода от ДНФ к СДНФ необходимо в каждый из членов, в которых представлены не все аргументы, ввести выражение вида , где xi — отсутствующий в члене аргумент. Так как , такая операция не может изменить значений функции. Покажем переход от ДНФ к СДНФ на примере следующего выражения:


Добавление в члены выражений вида приведет функцию к виду


На основании (3.1)
Отсюда после приведения подобных членов:

Полученная форма является СДНФ. Если исходная функция дана в табличной форме, то СДНФ может быть получена непосредственно.
Пусть дана функция в форме табл. 3.4. Для этой функции СДНФ имеет вид
|
| (3.10) |
| Таблица 3.4 | ||||||||
| x1 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 1 |
| x2 | 0 | 0 | 1 | 1 | 0 | 0 | 1 | 1 |
| x3 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 1 |
| f(x1,x2,x3) | 0 | 0 | 1 | 1 | 0 | 1 | 0 | 1 |
 Как видно из выражения (3.10), в нем каждый член соответствует определенному набору значений аргументов, при котором функция
Как видно из выражения (3.10), в нем каждый член соответствует определенному набору значений аргументов, при котором функция
 равна 1. Каждый из наборов аргументов, при которых равна 1 (3, 4, 6, 8-й столбцы наборов), обращает в единицу соответствующий член выражения (3.10), вследствие чего и вся функция оказывается раиной единице.
равна 1. Каждый из наборов аргументов, при которых равна 1 (3, 4, 6, 8-й столбцы наборов), обращает в единицу соответствующий член выражения (3.10), вследствие чего и вся функция оказывается раиной единице.
Можно сформулировать следующее правило записи СДНФ функции, заданной таблицей истинности.
Необходимо записать столько членов в виде конъюнкций всех аргументов, сколько единиц содержит функция в таблице. Каждая конъюнкция должна соответствовать определенному набору значений аргументов, обращающему функцию в единицу, и если в этом наборе значение аргумента равно нулю, то в конъюнкцию входит .инверсия данного аргумента.
Следует отметить, что любая функция имеет единственную СДНФ.
Совершенная конъюнктивная нормальная форма (СКНФ).
Конъюнктивной нормальной формой (КНФ) называется форма представления функции в виде конъюнкции ряда членов, каждый из которых является простой дизъюнкцией аргументов (или их инверсий).
Примером КНФ может служить следующая форма представления функции:


Приведем формы представления функций, не являющиеся КНФ:
(здесь третий член не является простой дизъюнкцией аргументов или их инверсий);

(эта форма также не является КНФ, так как в ней первый член не связан с остальными операцией конъюнкции).
В совершенной конъюнктивной нормальной форме (СКНФ) в каждом члене КНФ должны быть представлены все аргументы.

 Для перехода от КНФ к СКНФ необходимо добавить к каждому члену, не содержащему всех аргументов, члены вида , где хi — аргумент, не представленный в члене. Так как
Для перехода от КНФ к СКНФ необходимо добавить к каждому члену, не содержащему всех аргументов, члены вида , где хi — аргумент, не представленный в члене. Так как

 , то такая операция не может повлиять на значение функции.
, то такая операция не может повлиять на значение функции.
Добавление к некоторому члену образует выражение вида , которое можно привести к виду

Справедливость данного равенства вытекает из распределительного закона;
она может быть показана также путем раскрытия скобок в правой части выражения:



 так как
так как
Рассмотрим переход от КНФ к СКИФ на примере функции
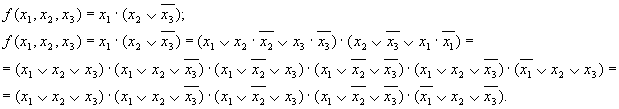


Покажем применение распределительного закона прн проведении использованных здесь преобразований над одним из членов выражения

Обозначим Тогда на основании распределительного закона
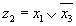


Далее обозначим и вновь применим распределительный закон
Подставив сюда значения z1 и z2 получим соответствующие члены приведенного выше выражения при переходе от КНФ к СКНФ.
Совершенная КНФ функции легко строится по таблице истинности.
Рассмотрим в качестве примера функцию, приведенную в табл. 3.4; СКНФ этой функции имеет вид
|
| (3.11) |
Выражение содержит столько членов, связанных операцией конъюнкции, сколько нулей имеется среди значений функции f(x1, x2, x3) в таблице истинности. Таким образом, каждому набору значений аргументов, на котором функция равна нулю, соответствует определенный член СКНФ, принимающий на этом наборе значение нуль. Так как члены СКНФ связаны операцией конъюнкции, при обращении в нуль одного из членов и вся функция оказывается равной нулю.
Таким образом, можно сформулировать следующее правило записи СКНФ функции, заданной таблицей истинности.
Следует записать столько конъюнктивных членов, представляющих собой дизъюнкции всех аргументов, при скольких наборах значений аргументов функция равна нулю, и если в наборе значение аргумента равно единице, то в дизъюнкцию входит инверсия этого аргумента. Любая функция имеет единственную СКНФ.
Структурная схема логического устройства может быть построена непосредственно по канонической форме (СДНФ или СКНФ) реализуемой функции. Получающиеся при этом схемы для функций (3.10) и (3.11) показаны на рис. 3.26, а и б. Недостаток такого метода построения структурных схем, обеспечивающего, в общем, правильное функционирование устройства, состоит в том, что получающиеся схемы, как правило, оказываются неоправданно сложными, требуют использования большого числа логических элементов и, следовательно, имеют низкие экономичность и надежность.
Во многих случаях удается так упростить логическое выражение, не нарушая функции, что соответствующая структурная схема оказывается существенно более простой.
Методы такого упрощения функции, называемые методами минимизации функций, рассматриваются ниже.

рис 3.26
Минимизация логических функций методом квайна
Метод Квайна относится к числу таких методов минимизации функции алгебры логики, которые позволяют представлять функции в ДНФ или КНФ с минимальным числом членов и минимальным числом букв в членах. Этот метод содержит два этапа преобразования выражения функции: на первом этапе осуществляется переход от канонической формы (СДНФ или СКНФ) к так называемой сокращенной форме, на втором этапе—переход от сокращенной формы логического выражения к минимальной форме.
Первый этап (получение сокращенной формы).
Пусть заданная функция f представлена в СДНФ.
Переход к сокращенной форме основан на последовательном применении двух операций: операции склеивания и операции поглощения.
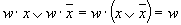
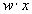
 Для выполнения операции склеивания выявляются в выражении пары членов вида и , различающихся лишь тем, что один из аргументов в одном из членов представлен без инверсии, в другом—с инверсией. Затем проводится склеивание таких пар членов: , и резуль-таты склеивания w вводятся в выражение функции в качестве дополнительных членов. Далее проводится операция поглощения. Она основана на равенстве
Для выполнения операции склеивания выявляются в выражении пары членов вида и , различающихся лишь тем, что один из аргументов в одном из членов представлен без инверсии, в другом—с инверсией. Затем проводится склеивание таких пар членов: , и резуль-таты склеивания w вводятся в выражение функции в качестве дополнительных членов. Далее проводится операция поглощения. Она основана на равенстве
 (член w поглощает член w? z). При проведении этой операции из логического выражения вычеркиваются все члены, поглощаемые членами, которые введены в результате проведения операции склеивания.
(член w поглощает член w? z). При проведении этой операции из логического выражения вычеркиваются все члены, поглощаемые членами, которые введены в результате проведения операции склеивания.
Операции склеивания и поглощения проводятся последовательно до тех пор, пока их выполнение оказывается возможным.
Покажем выполнение этих операций применительно к функции, представленной в табл. 3.5.
Записываем СДНФ функции
|
| (3.12) |
Попарным сравнением членов (каждого из членов со всеми последующими) выявляем склеивающиеся пары членов:

 первый и четвертый члены (результат склеивания );
первый и четвертый члены (результат склеивания );
 второй и третий члены (результат склеивания );
второй и третий члены (результат склеивания );
 второй и четвертый члены (результат склеивания );
второй и четвертый члены (результат склеивания );
 третий и пятый члены (результат склеивания ):
третий и пятый члены (результат склеивания ):
четвертый и пятый члены (результат склеивания ).
| Таблица 3.5 | ||||||||
| x1 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 1 |
| x2 | 0 | 0 | 1 | 1 | 0 | 0 | 1 | 1 |
| x3 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 1 |
| f(x1,x2,x3) | 0 | 0 | 1 | 1 | 0 | 1 | 0 | 1 |
Результаты операции склеивания вводим в выражение функции и проводим операцию поглощения ими членов исходного выражения: 

 Член поглощает те члены исходного выражения, которые содержат, т. е. первый и четвертый. Эти члены вычеркиваются. Член поглощает второй и третий, а член x1? x3 – пятый член исходного выражения.
Член поглощает те члены исходного выражения, которые содержат, т. е. первый и четвертый. Эти члены вычеркиваются. Член поглощает второй и третий, а член x1? x3 – пятый член исходного выражения.
Повторяем операции склеивания и поглощения:

Член операции склеивания
 Здесь склеивается лишь пара членов и , (склеивание пары членов и , приводит к тому же результату), результат склеивания х1, поглощает второй, третий, четвертый и пятый члены выражения.
Здесь склеивается лишь пара членов и , (склеивание пары членов и , приводит к тому же результату), результат склеивания х1, поглощает второй, третий, четвертый и пятый члены выражения.
Дальнейшее проведение операций склеивания и поглощения оказывается невозможным, сокращенная форма выражения заданной функции (в данном примере она совпадает с минимальной формой)
|
| (3.13) |
 Члены сокращенной формы (в рассмотренном примере такими членами служат и х1 называются простыми импликантами функции.
Члены сокращенной формы (в рассмотренном примере такими членами служат и х1 называются простыми импликантами функции.
Как видим, получено выражение существенно более простое по сравнению с СДНФ функции.
На рис. 3.27 приведена структурная схема логического устройства в базисе И, ИЛИ, НЕ, построенная с использованием выражения (3.13).
Второй этап (получение минимальной формы).
Сокращенная форма может содержать лишние члены, исключение которых из выражения функции не повлияет на значение функции.
Таким образом, дальнейшее упрощение логического выражения достигается исключением из выражения лишних членов. В этом и заключается содержание второго этапа минимизации. Покажем этот этап минимизации логического выражения на примере построения логического устройства для функции в табл. 3.6.
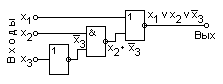
рис 3.27
| Таблица 3.6 | ||||||||||||||||
|
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
| 0 | 0 | 0 | 0 | 1 | 1 | 1 | 1 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 1 | |
| 0 | 0 | 1 | 1 | 0 | 0 | 1 | 1 | 0 | 0 | 1 | 1 | 0 | 0 | 1 | 1 | |
| 0 | 1 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 1 | |
| 1 | 1 | 1 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 |
Совершенная ДНФ.данной функции
|
| (3.14) |
Для получения сокращенной формы проводим операции склеивания и поглощения
Полученное выражение представляет собой сокращенную форму логического выражения заданной функции, а члены его — простые импликанты функции. Переход от сокращенной формы к минимальной осуществляется с помощью импликантной матрицы, приведенной в табл. 3.7.
В столбцы импликантной матрицы вписываются члены СДНФ заданной функции, в строки — простые импликанты функции, т. е. члены сокращенной формы логического выражения функции.
| Таблица 3.7 | ||||||
| Простые | Члены СДНФ | |||||
|
|
|
|
|
|
| |
|
| X | X | ||||
| X | X | |||||
| X | X | |||||
| X | X | |||||
| X | X |
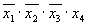

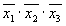 Отмечаются (например, крестиками) столбцы членов СДНФ, поглощаемых отдельными простыми импликантами. В табл. 3.7 простая импликанта поглощает члены , , и в первом и во втором столбцах первой строки поставлены крестики; вторая импликанта поглощает первый и третий члены СДНФ, и поставлены крестики в первом и третьем столбцах второй строки и т. д. Импликанты, которые не могут быть лишними и, следовательно, не могут быть исключены из сокращенной формы, составляют ядро. Входящие в ядро импликанты легко определяются по импликантной матрице. Для каждой из них имеется хотя бы один столбец, перекрываемый только данной импликантой.
Отмечаются (например, крестиками) столбцы членов СДНФ, поглощаемых отдельными простыми импликантами. В табл. 3.7 простая импликанта поглощает члены , , и в первом и во втором столбцах первой строки поставлены крестики; вторая импликанта поглощает первый и третий члены СДНФ, и поставлены крестики в первом и третьем столбцах второй строки и т. д. Импликанты, которые не могут быть лишними и, следовательно, не могут быть исключены из сокращенной формы, составляют ядро. Входящие в ядро импликанты легко определяются по импликантной матрице. Для каждой из них имеется хотя бы один столбец, перекрываемый только данной импликантой.
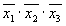
 В рассматриваемом примере ядро составляют импликанты и, (только ими перекрываются второй и шестой столбцы матрицы). Исключение из сокращенной формы одновременно всех импликант, не входящих в ядро, невозможно, так как исключение одной из импликант может превратить другую уже в нелишний член.
В рассматриваемом примере ядро составляют импликанты и, (только ими перекрываются второй и шестой столбцы матрицы). Исключение из сокращенной формы одновременно всех импликант, не входящих в ядро, невозможно, так как исключение одной из импликант может превратить другую уже в нелишний член.
 Для получения минимальной формы достаточно выбрать из импликант, не входящих в ядро, такое минимальное их число с минимальным количеством букв в каждой из этих импликант, которое обеспечит перекрытие всех столбцов импликантной матрицы, не перекрытых членами ядра. В рассматриваемом примере необходимо импликантами, не входящими в ядро, перекрыть третий и четвертый столбцы матрицы. Это может быть достигнуто различными способами, но так как необходимо выбирать минимальное число импликант, то, очевидно, для перекрытия этих столбцов следует выбрать импликанту . Минимальная дизъюнктивная нормальная форма (МДНФ) заданной функции
Для получения минимальной формы достаточно выбрать из импликант, не входящих в ядро, такое минимальное их число с минимальным количеством букв в каждой из этих импликант, которое обеспечит перекрытие всех столбцов импликантной матрицы, не перекрытых членами ядра. В рассматриваемом примере необходимо импликантами, не входящими в ядро, перекрыть третий и четвертый столбцы матрицы. Это может быть достигнуто различными способами, но так как необходимо выбирать минимальное число импликант, то, очевидно, для перекрытия этих столбцов следует выбрать импликанту . Минимальная дизъюнктивная нормальная форма (МДНФ) заданной функции
|
| (3.16) |
Структурная схема, соответствующая этому выражению, приведена на рис. 3.28.

рис 3.28
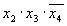


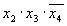
Переход от сокращенной формы (3.15) к МДНФ (3.16) был осуществлен путем исключения лишних имплнкант и . Покажем допустимость подобного исключения членов из логического выражения.
Импликанты и обращаются в единицу соответственно при следующих наборах значений аргументов:
x1 = 0; х2 = 0; х3 = 0 и х2 = 1; х3 = 1; х4 = 0 (3.17)
 Роль этих имликант в выражении сокращенной формы функции (3.15) заключается лишь в том, чтобы на приведенных наборах (3.17) значений аргументов присваивать функции значение 1. Однако при этих наборах функция имеет значение 1 из-за остальных импликант выражения (3.15). Действительно, подставляя значения (3.17) в (3.16), получаем:
Роль этих имликант в выражении сокращенной формы функции (3.15) заключается лишь в том, чтобы на приведенных наборах (3.17) значений аргументов присваивать функции значение 1. Однако при этих наборах функция имеет значение 1 из-за остальных импликант выражения (3.15). Действительно, подставляя значения (3.17) в (3.16), получаем:
при x1 = 0, x2 = 0, x3 = 0
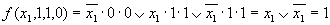
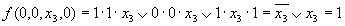
при х2 = 1; х3 = 1; х4 = 0
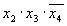

Таким образом, доказана справедливость операции исключения из выражения (3.15) членов и .
До сих пор рассматривалось получение минимальной ДНФ. При использовании метода Квайна для получения минимальной конъюнктивной нормальной формы (МК.НФ) логической функции имеются следущие особенности:
 исходной для минимизации формой логического выражения заданной функции является СКНФ;
исходной для минимизации формой логического выражения заданной функции является СКНФ;
 пары склеиваемых членов имеют вид и ;
пары склеиваемых членов имеют вид и ;
 операция поглощения проводится в соответствии с выражением
операция поглощения проводится в соответствии с выражением
Рассмотрим применение метода Квайна на примере минимизации функции, заданной таблицей истинности (табл. 3.8).
Совершенная КНФ рассматриваемой функции
 Склеивающиеся пары членов:
Склеивающиеся пары членов:
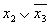 первый и третий члены (результат склеивания );
первый и третий члены (результат склеивания );
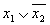 первый и четвертый члены (результат склеивания ):
первый и четвертый члены (результат склеивания ):
второй и третий члены (результат склеивания ).
| Таблица 3.8 | ||||||||
| x1 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 1 |
| x2 | 0 | 0 | 1 | 1 | 0 | 0 | 1 | 1 |
| x3 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 1 |
| f(x1,x2,x3) | 1 | 0 | 0 | 0 | 1 | 0 | 1 | 1 |
| Таблица 3.9 | ||||
| Простые | Члены СДНФ | |||
|
|
|
|
| |
|
| X | X | ||
| X | X | |||
| X | X |
Проводя операции склеивания и поглощения, получаем
Члены операции склеивания
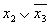
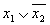
Полученное выражение явлиется сокращенной формой функции. Для перехода к минимальной форме строим иммлнк.шгную матрицу (табл. 3.9).
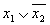
Все столбцы матрицы перекрываются импликантами и . Следовательно, член является лишним и минимальная конъюнктивная нормальная форма (МКНФ) заданной функции
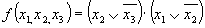
Минимизация логических функций методом карт Вейча
Метод Квайна имеет четко сформулированные правила проведения отдельных операций, благодаря чему он может быть использован для минимизации функций с использованием ЭВМ в тех случаях, когда минимизируемая функция достаточно сложна (содержит большое число аргументов и каноническая форма имеет большое число членов). Однако для минимизации функции ручным способом (без использования ЭВМ) этот метод оказывается весьма трудоемким. Трудоемкость метода Квайна связана с необходимостью попарного сравнения всех членов выражения для выявления склеиваемых членов.
Метод минимизации функции с помощью карт Вейча обеспечивает простоту получения результата. Он используется пои минимизации относительно несложных функций (с числом аргументов до 5) ручным способом. В отличие от метода Квайна этот метод требует элементов изобретательности и не может быть использован для решения задачи минимизации с помощью ЭВМ. Карга Вейча прдставляет собой определенную форму таблицы истинности. Табл. 3.10 являются картами Вейча для функций соответственно двух (а), трех (б), четырех (в) аргументов.
Каждая клетка карты соответствует определенному набору значений аргументов. Этот набор аргументов определяется присвоением значения лог. 1 буквам, на пересечении строк и столбцов которых расположена клетка. Так, в карте функций четырех аргументов (табл. 3.10,в) клегки первой строки соответствуют следующим комбинациям аргументов:
- первая клетка
- вторая клетка
- третья клетка
- четвертая клетка
Число клеток карты равно числу всех возможных наборов значений аргументов 2n (n – число аргументов функций). В каждую из клеток карты записывается значение функции на соответствующем этой клетке наборе значений аргументов. Пусть функция задана таблицей истинности в форме, которая использовалась ранее (табл. 3.11). Таблица истинности этой функции в форме карты Вейча представлена табл. 3.12.
Как видим, карта Вейча определяет значения функции на всех возможных наборах значений аргументов и, таким образом, является таблицей истинности. Карты Вейча компактны, но главное их достоинство состоит в следующем. При всяком переходе из одной клетки в соседнюю вдоль столбца или строки изменяется значение лишь одного аргумента функции. Следовательно, если в паре соседних клеток содержится 1, то над соответствующими им членами канонической формы может быть проведена операция склеивания. Таким образом, облегчается поиск склеиваемых членов.
| Таблица 3.12 | ||||||||
| x1 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 1 |
| x2 | 0 | 0 | 1 | 1 | 0 | 0 | 1 | 1 |
| x3 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 1 |
| f(x1,x2,x3) | 0 | 1 | 0 | 1 | 0 | 0 | 1 | 1 |
Сформулируем правила получения МДНФ функций с помощью карт Вейча.
Все клетки, содержащие 1, объединяются в замкнутые области. При этом каждая область должна представлять собой прямоугольник с числом клеток 2k, где k = 0, 1, 2, ... Таким образом, допустимое число клеток в области – 1, 2, 4, 8,... Области могут пересекаться и одни и те же клетки могут входить в разные области.
Затем проводится запись выражения МДНФ функции. Каждая из областей в МДНФ представляется членом, число букв в котором на k меньше общего числа аргументов функции n (т. е. равно n – k). Каждый член МДНФ составляется лишь из тех аргументов, которые для клеток соответствующей области имеют одинаковое значение (без инверсии либо с инверсией).
Таким образом, при охвате клеток замкнутыми областями следует стремиться, чтобы число областей было минимальным (при этом минимальным будет число членов в МДНФ функции), а каждая область содержала возможно большее число клеток (при этом минимальным будет число букв в членах МДНФ функции).
Рассмотрим минимизацию с помощью карты Вейча функции трех аргументов, представленной табл. 3.13.
 Все клетки, содержащие 1, охватываются двумя областями. В каждой из областей 21 клеток. Таким образом, для них n – k = 3 – 1 = 2 и эти области в МДНФ будут представлены членами, содержащими по две буквы. Первой обласги соответствует член x1? x2 (аргумент x3 здесь не присутствует, так как для одной клетки этой области он имеет значение без инверсии, для другой — с инверсией); второй области соответствует член . Следовательно, МДНФ функции
Все клетки, содержащие 1, охватываются двумя областями. В каждой из областей 21 клеток. Таким образом, для них n – k = 3 – 1 = 2 и эти области в МДНФ будут представлены членами, содержащими по две буквы. Первой обласги соответствует член x1? x2 (аргумент x3 здесь не присутствует, так как для одной клетки этой области он имеет значение без инверсии, для другой — с инверсией); второй области соответствует член . Следовательно, МДНФ функции
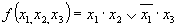
Рассмотрим пример минимизации функции четырех аргумен. тов. заданной табл. 3.14.
Первая и четвертая области имеют по две клетки, для них n – k = 4 – 1 = 3. Эти области будут в МДНФ представлены членами, содержащими по три буквы.
Вторая и третья области содержат по четыре клетки и в МДНФ выражаются членами, содержащими по две буквы (n – k = 4 – 2 = 2).
Минимальная ДНФ функции имеет вид
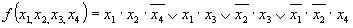
При построении замкнутых областей допускается сворачивание карты в цилиндр с объединением се противоположных граней. В силу этого крайние клетки строки или столбца таблицы рассматриваются как соседние и могут быть объединены в общую область, Иллюстрацию этого приема проведем на примере функции, представленной табл. 3.15, Минимальная ДНФ функции
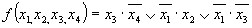
В силу допустимости такого сворачиванья карты вдоль горизонтальной и вертикальной осей, например, клетки, расположенные н четырех углах карты функции четырех переменных, оказываются соседними и могут быть объединены в одну область. Покажем это на примере минимизации функции, заданной табл. 3.16. Минимальная ДНФ функции

Для получения МКНФ функции замкнутыми областями охватываются клетки с нулевыми значениями функции, и при записи членов логического выражения берутся инверсии аргументов, на пересечении которых находятся области. Так, для функции, приведенной в табл. 3.17, МКНФ

| Таблица 3.17 |
|
|
До сих пор здесь рассматривались логические функции с числом аргументов до четырех. Представление функции и минимизация ее с помощью карт Вейча усложняются, если число аргументов больше четырех.
В табл. 3.18 показано представление с помощью карт Вейча функции пяти аргументов.
Таблица истинности здесь состоит из двух карт, каждая из которых представляет собой карту четырех переменных. Одна из них соответствует x5 = 1, другая – x5 = 0, Эти карты можно мысленно представить себе расположенными одна над другой (рис. 3.29). При этом области охвата клеток могут быть трехмерными, т. е. одной областью могут охватываться клегки двух карт.
Для приведенной в табл. 3.18 функции МДНФ равна

Для минимизации функций с числом аргументов, большим пяти, карты Вейча оказываются неудобными. Минимизация таких функций может быть выполнена методом Квайна.
Синтез не полностью заданных логических функций
По условиям работы логического устройства может оказаться, что некоторые наборы значений аргументов являются запрещенными для данного устройства и никогда не могут появляться на его входах. В этом случае функция оказывается заданной не на всех наборах аргументов. Такие функции будем называть не полностью заданными.
При синтезе логического устройства, реализующего не полностью заданную функцию, допустимо произвольно задаваться значениями функции на запрещенных наборах аргументов. При этом в заннсимости от способа задания этих значений функции минимальная фирма может оказаться простой или более сложной. Таким образом, возникает проблема целесообразного доопределения функции на запрещенных наборах аргументов.
Может быть использован следующий способ получения минимальной формы не полностью заданной функции f:
а) записывается СДПФ (СКИФ) функции f0. полученной из f путем задания значения 0 (значения 1 и случае СНКФ) на всех запрещенных наборах аргументов;
б) записывается СДНФ (СКИФ) функции f1, полученной из f путем задания значения 1 (значения 0 в случае СКНФ) на всех запрещенных наборах аргументов;
в) функция f1 приводится к сокращенной форме (к форме, содержащей все простые имплнканты);
г) составляется импликантнзя таблица из всех членов функции f0 и простых импликант функции f1;
д) искомая минимальная форма составляется из простых импликант функции f1, поглощающих все члены СДНФ (СКНФ) функции f0.
Рассмотрим применение данного метода к минимизации не полностью заданной функции, приведенной в табл. 3.19,
Записываем логическое выражение функции f0 в СДНФ

Записываем СДНФ функции f1
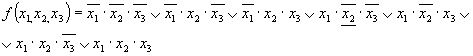
Методом Квайна приводим функцию f1 к сокращенной форме:
Составляем импликантную таблицу (табл. 3.20).
| Таблица 3.19 | ||||||||
| x1 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 1 |
| x2 | 0 | 0 | 1 | 1 | 0 | 0 | 1 | 1 |
| x3 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 1 |
| f(x1,x2,x3) | * | 0 | 1 | * | 1 | * | * | 1 |
| Таблица 3.20 | |||
| Простые | Члены СДНФ | ||
|
|
|
| |
|
| X | X | |
| X | X | ||
| X | X |
Минимальная форма логического выражения функции может быть получена исключением любой из трех простых импликант
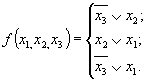
Рассмотрим минимизацию той же функции методом карты Вейча (табл. 3.21).
При минимизации функции данным методом следует на запрещенных наборах аргументов задавать функции такие значения, при которых клетки со значением 1 (либо 0) охватываются минимальным числом областей с максимальным числом клеток в каждой из областей. Применительно к рассматриваемся функции такое доопределение функции может быть осуществлено тремя различными способами, представленными в табл. 3.22. Они приводят к полученным выше выражениям МДНФ функции.
Синтез логических устройств с несколькими выходами
Пусть синтезируемое логическое устройство имеет п входов и т выходов (рис. 3.30). На каждом из выходов должна быть сформирована определенная функция входных переменных.
Эта задача могла бы быть решена синтезированием раздельно действующих узлов, каждый из которых реализовывал бы определенную выходную функцию. Однако, если даже каждый из этих узлов будет построен минимальным образом, в целом логическое устройство может оказаться не минимальным. Действительно, такое устройство могло бы быть подвергнуто минимизации путем использования общих элементов и нескольких устройствах, реализующих различные выходные функции.
Из этих соображений принеленне каждой из выходных функций к минимальной форме не является услонисм получения минимального в целом устройства. При минимизации устройств и целим некоторые нз функций могут оказаться представленными и неминимальной форме.
Принцип получения минимальной формы устройства сводится к нахождению минимального набора членов с минимальным числом входящих в них букв, достаточного для получения всех формируемых устройством функций.
Метод построения минимальных логических устройств с несколькими выходами рассмотрим на примере реализации устройства, способ функционирования которого задан табл. 3.23.
Записываем наборы аргументов, на которых хотя бы одна из выходных функций имеет значение 1, Рядом в таблице в качестве признака записываем функции, принимающие значения 1 при данном наборе аргументов (табл. 3.24).
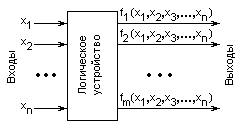
рис 3.24
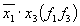


 Затем проводим операцию склеивания и получающиеся при этом члены заносим в табл. 3.25, рядом с членами записываем признаки в виде функций, общих в признаках той пары членов табл. 3.24, склеиванием которых они получены. Так склеивание членов табл. 3.24 и
Затем проводим операцию склеивания и получающиеся при этом члены заносим в табл. 3.25, рядом с членами записываем признаки в виде функций, общих в признаках той пары членов табл. 3.24, склеиванием которых они получены. Так склеивание членов табл. 3.24 и
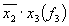
 Приводит в табл. 3.25 к члену ; склеивание членов
Приводит в табл. 3.25 к члену ; склеивание членов
и приводит к и т. д.
| Таблица 3.23 | ||||||||
| X1 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 1 |
| X2 | 0 | 0 | 1 | 1 | 0 | 0 | 1 | 1 |
| X3 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 1 |
| f1(x1,x2,x3) | 0 | 1 | 0 | 1 | 0 | 0 | 1 | 1 |
| f2(x1,x2,x3) | 0 | 0 | 1 | 0 | 1 | 1 | 0 | 0 |
| f2(x1,x2,x3) | 0 | 1 | 1 | 1 | 1 | 1 | 0 | 0 |
| Таблица 3.25 | |
|
| f1f3 |
| f3 | |
| f3 | |
| f1 | |
| f2f3 | |
| f1 |
Не проводится операция склеивания над членами, в признаках которых не имеется общих функций.
Далее проводится операция поглощения членами табл. 3.25 членов табл. 3.24. Операция поглощения может проводиться лишь над членами, имеющими одинаковую комбинацию функций в признаках.
Указанные операции склеивания и поглощения повторяются, пока их проведение оказывается возможным. Затем составляется импликантная таблица (табл. 3.26). Определяется набор импликант, обеспечивающий перекрятие всех столбцов импликантной таблицы. Этот набор импликант приведен в табл. 3.27.
Записываем логические выражения для выходных функций, составленные из этих импликант, в признаках которых содержатся заданные функции:

| Таблица 3.26 | |||||||||||||
|
|
|
|
|
|
|
| |||||||
| f1 | f3 | f2 | f3 | f1 | f3 | f2 | f3 | f2 | f3 | f1 | f1 | ||
|
| (f2f3) | X | X | ||||||||||
| (f1f3) | X | X | X | X | |||||||||
| (f3) | X | X | |||||||||||
| (f3) | X | X | |||||||||||
| (f1) | X | ||||||||||||
| (f2f3) | X | X | X | X | |||||||||
| (f1) | X | X |

Легко убедиться, что выражение для функции не является минимальным. Минимальная для этой функции форма
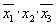

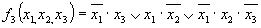

Однако замена в выражении функции f3 члена членом
невыгодна, так как член присутствует и в выражении f2 и он должен быть сформирован для этой функции.
На рис. 3.31 приведена функциональная схема устройства, обеспечивающего заданное табл. 3.23 функционирование. Как нидно из схемы, ряд элементов участвует одновременно в формировании нескольких выходных функций.
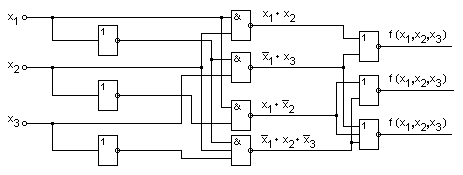
рис 3.31
Синтез логических устройств в базисе ИЛИ_НЕ и И-НЕ
Построение логического устройства на элементах ИЛИ-НЕ может быть выполнено при следующей последовательности действий: заданная функция минимизируется с получением МКНФ; производится запись полученного логического выражения через операции ИЛИ-НЕ.
Рассмотрим последовательность синтеза на примере построения логического устройства, реализующего функцию, приведенную в табл. 3.28.
Для минимизации функции воспользуемся методом Вейча. В табл. 3.29 приведена карта Вейча для рассматриваемой функции.
| Таблица 3.28 | ||||||||||||||||
|
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
| 0 | 0 | 0 | 0 | 1 | 1 | 1 | 1 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 1 | |
| 0 | 0 | 1 | 1 | 0 | 0 | 1 | 1 | 0 | 0 | 1 | 1 | 0 | 0 | 1 | 1 | |
| 0 | 1 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 1 | |
| 0 | 0 | 1 | 1 | 0 | 0 | 0 | 1 | 1 | 1 | 0 | 0 | 1 | 1 | 0 | 1 |
Минимальная КНФ функции
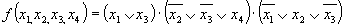
Для перехода от базиса И, ИЛИ, НЕ, в котором представлено полученное логическое выражение, к базису ИЛИ-НЕ проводим следующие действия:
дважды инвертируем правую часть выражении

проводим преобразование по формуле де Моргана
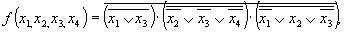
записываем выражение с использованием символа операции ИЛИ-НЕ
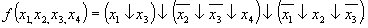
Заметим, что в (3.18) наличие поставленных скобок обязательно, иначе исказится функция.
Построенная в соответствии с (3.18) схема логического устройства приведена на рис. 3.32.
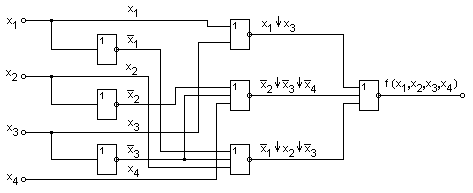
рис 3.32

рис 3.33
Методика синтеза устройства в базисе И-НЕ сходна с рассмотренной выше методикой синтеза в базисе ИЛИ-НЕ. Имеющиеся особенности рассмотрим на примере построения с использованием элементов И-НЕ логического устройства, реализующего функцию, заданную таблицей истинности (табл. 3.28).
Минимизируем функцию. В отличие от синтеза в базисе ИЛИ-НЕ, при котором в процессе минимизации получают МКНФ функции, при синтезе в базисе И-НЕ должна быть получена МДНФ функции. Минимизацию проведем с помощью карты Вейча (табл. 3.30).
Минимальная ДНФ функции
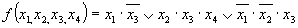
Дважды инвертируем правую часть выражения
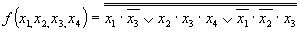
Проводим преобразование по формуле де Моргана
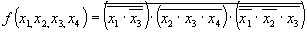
Записываем выражение с использованием символа операции И-НЕ
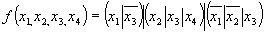
Выражению (3.20) соответствует схема, приведенная на рис. 3.33
Некоторые особенности построения схем логических устройств
Построенная структурная схема логического устройства может содержать элементы с разным числом входов. Так, в схеме на рис. 3.33 используются, кроме инверторов, элементы И-НЕ с двумя и тремя входами. В выпускаемых промышленностью сериях элементов обычно предусматриваются элементы с разным числом входов. Поэтому для построения устройств в большинстве случаев могут быть использованы элементы точно с тем же числом входов, какое требуется в отдельных элементах структурной схемы.
Иногда по разным соображениям приходится использовать в схеме элементы, число входов у которых больше или меньше чем то, которое требуется при рассмотренных выше способах синтеза устройств. Ниже рассматриваются возникающие в этих случаях особенности построения устройств.
Рассмотрим использование элементов, имеющих избыточное число входов. Для определенности примем, что элементы имеют три входа, причем для подачи входных переменных требуется лишь два входа. Избыточный вход мог бы быть оставлен свободным (не подключенным к каким-либо цепям), как это показано на рис. 3.34,а. Однако для уменьшения влияния наводимых на этот вход помех нежелательно неиспользуемый вход оставлять свободным. При этом возможны следующие способы его включения.
Неиспользуемый вход может быть подключен к любому из используемых входов (рис. 3.34,б). Недостаток такого способа соединения состоит в следующем. Объединение входов приводит к тому, что к выходу источника входного сигнала (т. е. к выходу предыдущего элемента, с которого сигнал подается на вход данного элемента) оказывается подключенным большее число входов элемента. Такое возрастание нагрузки вызывает увеличение задержки распространения сигнала, снижение быстродействия элемента.
Поэтому наиболее удачным следует считать способ, при котором на неиспользуемый вход подается логическая константа 0 или 1 (т. е. потенциал, соответствующий логической константе 0 либо 1). Такой способ соединения показан на рис. 3.34,в. Здесь на свободные входы элементов ИЛИ и ИЛИ-НЕ подается постоянный потенциал уровня, соответствующего лог. 0, а для элементов И и И-НЕ – потенциал уровня, соответствующего лог. 1.
Теперь рассмотрим более сложный случай построения устройства на элементах с недостающим числом входов.
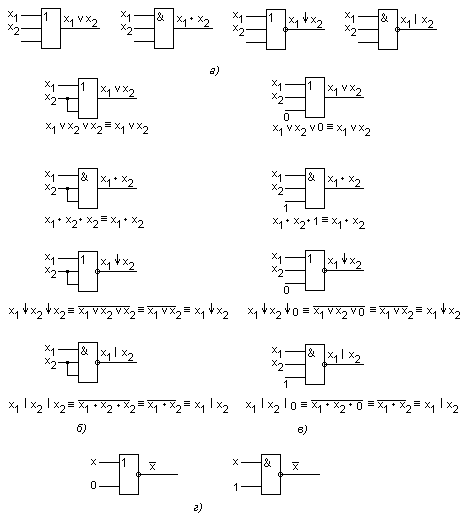
рис 3.34
На рис. 3.35 показан способ реализации 3х буквенного члена логического выражения функции на различных типах элементов с двумя входами.
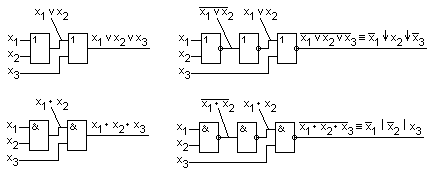
рис 3.35
В логическом выражении может оказаться несколько членов с числом букв, превышающим число входов элементов. В этом случае для уменьшения числа используемых элементов следует провести соответствующее преобразование групп членов. Этот прием покажем на примере реализации рассмотренной выше логической функции (3.20). Пусть требуется построить устройстоо, реализующее функцию (3.20) на двухвходовых элементах И-НЕ. Обратимся к (3.19). В нем сгруппируем два последних члена, вынеся за скобки x3:

К полученному выражению применим формулу де Моргана
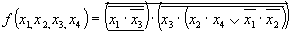

Пользуясь формулой де Моргана, можно преобразовать к виду
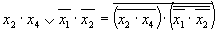
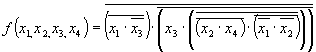
После подстановки в предыдущее выражение получим
Запишем данное выражение через операцию И-НЕ:

Построенная в соответствии с этим выражением схема приведена на рис. 3.36.
Из сравнения схем ва рис. 3.33 и 3.36 видно, что синтез устройств на элементах с уменьшенным числом входов вызвал необходимость применения большего числа элементов.
Изложенным приемом удается пользоваться не всегда. Например, им невозможно воспользоваться в случаях, когда члены МДНФ не содержат общих букв. При этом необходимое преобразование логического выражения достигается с использованием тождественного соотношения:
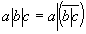
Покажем справедливость этого тождества


рис 3.36
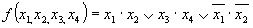
Пусть требуется синтезировать с использованием двухвходо-вых элементов И-НЕ логическую функцию, МДНФ которой представляется выражением . Записываем выражение через операцию И-НЕ:
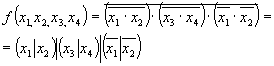
Применяя к данному выражению преобразование (3.21), получим

Построенная в соответствии с данным выражением функциональная схема логического устройства приведена на рис. 3.37.
Рассмотрим реализацию на двухвходовых элементах И-НЕ функции

Перейдем к операции И-НЕ и затем применим соотношение (3.21):

Люди также интересуются этой лекцией: 28 - Эталонная модель взаимодействия открытых систем.
Аналогичное (3.21) преобразование для случая, когда предполагается реализация логического устройства в базисе ИЛИ-НЕ, имеет вид
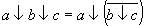
Покажем справедливость этого тождественного соотношения:

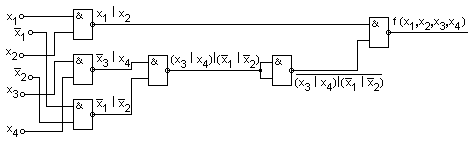
рис 3.37