Задачи по разделам курса

1. Дополнительные материалы: Задачи по разделам курса

Языки и их представление

Алфавиты, цепочки и языки

1. Пусть A = {ab, c} и B = {c, ca} - два формальных языка над алфавитом {a, b, c}. Найти следующие формальные языки:
1. AB;
2. A B;
3. A²;
4. A² B²;
5. AB.

Представление языков

• Для языка L = {x {a, b}*||x|_a - чeтное, |x|_b - нечeтное} постройте
1. Детерминированный конечный автомат;
2. По нему - регулярное выражение;
3. По этому выражению - грамматику;
4. По полученной грамматике перейдите по GN-теореме к N- автомату.

Грамматики

2.3.1. Принадлежит ли цепочка x = abaababb языку, порождаемому грамматикой с правилами:

S  SaSb|ε

2.3.2. Принадлежит ли цепочка x = (()())() языку, порождаемому грамматикой с правилами:

S  SA|A

Рекомендуемые материалы

A  (S)|()

2.3.3. Принадлежит ли цепочка x = 00011011 языку, порождаемому грамматикой с правилами:

S  SS|A

A  0A1|S|01

2.3.4. Принадлежит ли цепочка x = 0111000 языку, порождаемому грамматикой с правилами:

S  A0B|B1A

A  BB|0

B  AA|1

2.3.5. Верно ли соотношение a*cb* 2 L(G) для следующей грамматики G?

S  Bab|aDa; A  Dc|cA; B  Sb|b;

D  AB|aD.

2.3.6. Верно ли соотношение ab*c* 2 L(G) для следующей грамматики G?

S  SAS|A; A  Ac|Da|b; B  DaD;

D  ABD|AB.

2.3.7. Верно ли соотношение ca*b* 2 L(G) для следующей грамматики G?

S  bcD|aB; A  Db|cA; B  bS|ε;

D  BA|cD.

2.3.8. Верно ли соотношение c*ab* 2 L(G) для следующей грамматики G?

S  ASS|A; A  c|Ab|aD; B  aDD;

D  AB|BaB.

2.3.9. Пусть грамматика G определяется правилами

S  AB; AB  CBb; CB  ABB;

A  a; aB  a:

Какому классу (по Хомскому) она принадлежит? Порождается ли L(G) грамматикой более узкого класса?

2.3.10. Пусть грамматика G определяется правилами

S  aAbB; AbB  aAbB; bBb  bb; A  ε.

Какому классу (по Хомскому) она принадлежит? Порождается ли L(G) грамматикой более узкого класса?

2.3.11. Пусть грамматика G определяется правилами

S  AaB; AaB  aAaBb; aBb  abb; A  ε.

Какому классу (по Хомскому) она принадлежит? Порождается ли L(G) грамматикой более узкого класса?

2.3.12. Пусть грамматика G определяется правилами

S  AB; AB  aDB; DB  ABB; B  b; Ab  b.

Какому классу (по Хомскому) она принадлежит? Порождается ли L(G) грамматикой более узкого класса?

2.3.13. Какому классу по Хомскому принадлежит:

а) Грамматика с правилами:

S  AS|ε; A  a|b:

б) Язык, порождаемый этой грамматикой?

2.3.14. Какому классу по Хомскому принадлежит:

а) Грамматика с правилами:

S  AB; AB  aABB; B  b; A  a;

б) Язык, порожденный этой грамматикой?

2.3.15. Какому классу по Хомскому принадлежит:

а) Грамматика с правилами:

S  ASB|BSA; A  a; B  b|ε; SB  ε;

б) Язык, порожденный этой грамматикой?

2.3.16. Какому классу по Хомскому принадлежит:

а) Грамматика с правилами:

S  AcBs; A  AcA|B; B  a|b;

б) Язык, порождeнный этой грамматикой?

2.3.17. Сколько существует различных выводов цепочки baaaab, принадлежащей языку, порождаемому грамматикой с правилами:

S  bAb; A  AA|a

2.3.18. Построить праволинейные грамматики для языков, состоящих из:

а) идентификаторов произвольной длины, начинающихся с буквы;

б) идентификаторов, содержащих от 1 до 6 символов и начинающихся с букв I, J, K, L, M, N;

в) вещественных констант;

г) всех цепочек из нулей и единиц, имеющих:

- чeтное число нулей и чeтное число единиц;

- либо нечeтное число нулей и нечeтное число единиц.

2.3.19. Построить КС-грамматики для следующих языков:

а) {0ⁿ1ⁿ : n  1

б) {ww^R : w {a, b}^*}

в)  Вcе цепочки из нулей и единиц с одинаковым числом тех и

других

г) {{a, b}^* {a^mbⁿa^mbⁿ} : m, n  1};

д) {{a, b}^* {a^2mb³ⁿa^2mbⁿ} : m, n  1};

е) {{a, b}^* {a^mbⁿa^m} : m, n  1};

ж) {{a, b}^* {ww} : w  {a, b^*};

з) {{a, b}^* {aⁿbⁿaⁿ} : n  1};

2.3.20. Определить КС-грамматики, которые порождали бы следующие языки:

1) все строки - элементы множества {0, 1}* такие, что в каждой из них непосредственно справа от каждого символа 0 стоит символ 1.

2) все строки - элементы множества {0, 1}* такие, что результаты чтения этих строк слева направо и справа налево совпадают;

3) все строки - элементы множества {0, 1}*, которые содержат символов 0 вдвое больше, чем символов 1;

4) все строки - элементы множества {0, 1}*, которые имеют одинаковое число символов 0 и 1;

5) все строки - элементы множества {0, 1}*, которые имеют четное число символов 0 и нечетное число символов 1;

6) все строки - элементы множества {0, 1}*, в которых скобки расставлены правильно.

2.3.21. Построить КС-грамматики, порождающие языки:

а) {a^mbⁿc^p|m + n + p  0(mod 2); m, n, p  0};

б) {a^pb^qc^r|p + q > r; p, q, r  0};

в) {x|x  {a, b}*, |x|_a = |x|_b};

г) {x|x  {a, b}*, |x|_a > |x|_b};

д) построить однозначную КС-грамматику (однозначность

должна быть доказана) для языка {x|x  {a, b}*, |x|_a = |x|_b,

и для  u, v : x = uv; |u|  0, |v|  0 выполнено |u|_a > |u|_b}.

2.3.22. Построить КС-грамматику, порождающую язык

а) {aⁿcbⁿ}  {bⁿacⁿ}; n  0

б) {x|x  {a, b}* ε; x  yy^R}

2.3.23. Построить НС-грамматики для следующих языков:

а) {w {a, b, c}*, |w|_a = |w|_b = |w|_c} (Винегрет)

б) {w {a, b, c}*, 3|w|_a = 5|w|_b = 7|w|_c} (Винегрет 2)

в) {aⁿpⁿrⁿ} : n ; 1} (Три мушкетeра)

г) {a^mbⁿa^mbⁿ : m, n 1} (Две калоши)

д) {a^2mbⁿa^mb⁵ⁿ : m, n 1} (Калоши 2)

е) {a^mbⁿc^k : m n k 1} (Горка)

ж) {a^mbⁿc^k : 2m 3n k 1} (Горка 2)

з) (Бог любит троицу)

и)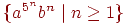

к) (Квадратные числа)

л)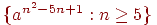

м) (Дама с собачкой)

н)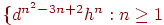

о) {aⁿ : n = 1, 2, 3, 5, 8, 13, ...} (Числа Фиббоначи)

п) {an : n = 1, 3, 6, 10, 15, ...} (Треугольные числа, a_n = n(n + 1)/2)

р) {aⁿ : n = 1, 5, 12, 22, ...} (Пятиугольные числа, a_n = n + 3n(n - 1)/2. Пятиугольное число может быть разбито на три треугольных + n точек)

с) {ww : w {a, b}^*} (Два лебедя)

т) (Кубические числа)

у)

ф) {aⁿ : n = 1, 2, 6, 24, ... , k!} (Факториал)

х) {01²...0^n-11ⁿ0^n-1...1²0|n 1} (Пирамида Хеопса)

ч) {01²...0^n-11ⁿ1ⁿ0^n-1...1²0|n 1} (Пирамиды майя)

ш)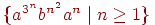

щ) (Для студентов с исследовательской жилкой).

2.3.24. Построить КС-грамматики, порождающие языки

а) {xcy|x  y;  x, y  {a, b}^*};

б) {aⁱb^jc^k|i, j, k  1} {aⁿbⁿcⁿ|n  1};

в) {a, b, c}^* {aⁿbⁿcⁿ|n  0}.

2.3.25. Пусть G - грамматика с правилами:

S  CD                C  aCA|bCB|ε         AD  aD

BD  bD       Aa  aA               Ab  bA

Ba  aB       Bb  bB               D  ε

Показать, что L(G) = {xx|x {a, b}^*}.

2.3.26. Построить грамматику, порождающую данный язык:

{aⁿcbⁿaⁿcbⁿ|n > 0}:

2.3.27. Построить регулярную грамматику, порождающую цепочки в алфавите (a, b), в котором символ a не встречается два раза подряд.

2.3.28. Построить грамматику, порождающую сбалансированные относительно круглых скобок цепочки в алфавите Сбалансированную цепочку определим реккурентно: цепочка сбалансирована, если:

а) не содержит скобок,

б) = (₁) или = ₁₂, где ₁ и ₂ сбалансированы.

2.3.29 Показать, что наличие в КС-грамматике правил вида

а) A AA| б) A AA|β в) A A|Aβ|γ, где , β, γ (V_N V_T)^*; A V_N, делает еe неоднозначной. Можно ли преобразовать эти правила таким образом, чтобы полученная эквивалентная грамматика была однозначной?

2.3.30. Показать, что грамматика G неоднозначна.

 

G : S  abC|aB B  bc; bC  bc

2.3.31. Дана КС-грамматика G = (VT, VN, P, S). Предложить алгоритм построения множества

X = {A  V_N|A ε}.

2.3.32. Для произвольной КС-грамматики G предложить алгоритм, определяющий, пуст ли язык L(G).

2.3.33. Одинаковые ли языки порождают грамматики из а), б), в)?

а) S  aAb    A  BB        B  ab|A|ε;

б) S  aAb    A  AaAb|ε;

в) S  aB     B  aBB|b.

2.3.34. Эквивалентны ли грамматики с правилами

S  AB; B  Bb|A; A  Aa|B; C  c.

и

S  ε.

2.3.35. Эквивалентны ли грамматики с правилами

A  AB; B  bC; A  aAc|Sa; C  c|Ca.

и

S  As|Bc; B  Ac|cS; A  Bd; C  c.

Лексический анализ

Регулярные множества и выражения

3.1.1. Показать, что множества, соответствующие двум данным регулярным выражениям, совпадают,

1) (a*b)c и a*(bc);            2) a*b и b + aa*b;

3) b(b + ab)*a и b(b*ab)*b*a; 4) b(ab + b)* и bb*a(bb*a)*:

  

3.1.2. Заменить каждое из следующих выражений эквивалентным, в котором не используются знак "+":

1) (a + b)*;

2) (a + bb + ba)*;

3) (a + (bb + ab)*)*:

3.1.3. Найти регулярные выражения, обозначающие языки, все слова которых - элементы множества {0, 1}^*:

1) оканчивающиеся на 011, 101, 110;

2) начинающиеся с 110, 101 или 011;

3) у которых каждый третий символ есть 0 или каждым

второй - 1;

4) не содержащие ни одной из подстрок 011 и 101;

5) содержащие каждую из подстрок 011 и 101;

6) начинающиеся с 011 и оканчивающиеся на 110 или 101;

7) начинающиеся с 011 или 110 и оканчивающиеся на 101;

8) начинающиеся с 011 и содержащие вхождения подстроки

110;

9) {01ⁿ|n > 1};

10) {01ⁿ0|n > 0};

11) {0^m1ⁿ|n, m > 1};

12) {  {0, 1}* : ||=3 - целое неотрицательное число};

13) {a|  {0, 1}⁺, a  {0, 1}, a входит в };

14) {(010)ⁿ|n > 0};

15) {0^m|m > 2} или {1ⁿ|n > 0};

16) {(01)^m(10)ⁿ|m  0, n  0};

17) содержащее четное число символов 0 и нечетное число

символов 1;

18) содержащее четное число символов 0 или четное число

символов 1.

  

3.1.4. Является ли язык, состоящий из всех цепочек из 0 и 1, не содержащих подцепочки 010, регулярным?

3.1.5. Является ли язык, состоящий из всех цепочек из 0 и 1, содержащих чeтное число 0 и нечeтное - 1, регулярным?

3.1.6. Является ли язык, состоящий из всех цепочек чeтной длины в алфавите{fa, b, c}, регулярным?

3.1.7. Регулярен ли

а) язык формул вида A*(B), где A, B  {a, b}⁺?

б) язык формул вида (A₁.A₂), где для i = 1,  A_i есть либо

слово в алфавите {a, b}, либо, в свою очередь, формула?

в) язык формул вида (A + B), где A, B  {a, b}⁺?

г) язык формул вида (A₁)A₂, где для i = 1,  A_i есть либо

слово в алфавите {a, b}, либо, в свою очередь, формула?

3.1.8. Определить язык, состоящий из всех идентификаторов, с помощью:

а) регулярного выражения;

б) леволинейной грамматики;

в) конечного автомата;

г) праволинейной грамматики.

3.1.9. Будет ли регулярным язык L = {x {a, b}^* : |x|_a четно и |x|_b нечетно}?

3.1.10. Построить праволинейную грамматику, порождающую язык L всех слов в алфавите {0, 1}, содержащих чeтное число единиц и нечeтное число нулей. Будет ли она однозначной?

3.1.11. Построить регулярное выражение для языка L^R, где L - язык всех слов в алфавите {0, 1}, содержащих чeтное число единиц и нечeтное число нулей.

Конечные автоматы

3.2.1. Какой язык допускается конечным автоматом M = ({q₀}, {a, b}, , q₀, {q₀})?

3.2.2. Построить недетерминированный конечный автомат, допускающий цепочки в алфавите {1, 2}, у которых последний символ цепочки уже появлялся в ней раньше. Построить эквивалентный детерминированный конечный автомат. Построить аналогичные конечные автоматы в алфавите {1, 2, 3}.

3.2.3. Построить конечный автомат, допускающий язык {xy} {yx}, где x {a}^* ε y {b}^* ε.

3.2.4. Построить детерминированный конечный автомат, допускающий язык L всех слов в алфавите {0, 1}, содержащих чeтное число единиц и нечeтное число нулей;

Алгоритмы построения конечных автоматов

3.3.1. Для регулярного выражения над алфавитом T = {a, b} построить эквивалентный детерминированный конечный автомат:

а) b(ba|b)*|b          б) (ab|b)*ba|ab

в) (a|b)*ba(a|b)       г) (a|b)*ab(a|b)*

д) a(ab|b)*|ba         е) (ba|b)*ab|ba

ж) (a*b)*ab*a          з) (a|b)*(a|b)(a|b(a|b)

Лексический анализ

Регулярные множества и их представления

3.4.1. Будет ли регулярным язык L = {x {a, b}|x не содержит подцепочки aba}?

3.4.2. Возможно ли построить регулярную грамматику, порождающую язык, включающий в себя все непустые цепочки из 0 и 1, не содержащие трeх 1 подряд?

Алгебраические свойства регулярных множеств. Лемма о разрастании.

3.5.1. Будут ли регулярными следующие языки в алфавите {a}:

а) L₁ = {{a²ⁿ⁺⁵} {a⁷ⁿ⁺⁴}, n = 0, 1, ...};

б) L₂ = {{a²ⁿ⁺⁵} {a⁷ⁿ⁺⁴}, n = 0, 1, ...};

в) L₃ = {{a⁴ⁿ⁺⁵}, n = 0, 1, ..., n 5(mod11)};

д) .

3.5.2. Будут ли регулярными следующие языки в алфавите Σ = {a, b}:

а) язык L₁ из всех слов Σ*, содержащих подслова a?b;

б) язык L₂ из всех слов Σ*, не содержащих двух b подряд;

в) язык L₃ из всех слов Σ*, не принадлежащих L₁ или L₂;

г) L₄ = {{a²ⁿ⁺⁵b⁷ⁿ⁺⁴}, n = 0, 1, ...}?

3.5.3. Задается ли язык {aⁿb^m|n m 1} регулярным выражением?

3.5.4. Является ли грамматика с правилами:

S  aA|bB|C; B  bB|b|ε;

A  aA|a|ε;   C  cSC:

праволинейной грамматикой?

Синтаксический анализ

КС-грамматики и МП-автоматы

4.1.1. Пусть G - грамматика с правилами:

S  SbS|ScS|a

Найти 2 различных дерева вывода для цепочки abaca.

4.1.2. Дана однозначная КС-грамматика G = (N, T, P, S) и цепочка w L(G). Количество элементов во множествах N, T, P равно n₁, n₂, n₃ соответственно, а |w| = l. Найти нижнюю и верхнюю границу для числа деревьев разбора w в G.

4.1.3. Являются ли однозначными следующие грамматики?

а) S  a|C; C  AB; A  aA|Ba|a; B  aB;

б) S  BA; A  Aa|bA|ε; B  Bb|aB|b;

в) S  b|C; C  aC|AC; A  aA|Aa|a;

г) S  AB; A  aA|bA|a; B  Ba|Bb|ε;

д) S  A|B; A  AA|a; B  aB|b|C; C  cC;

е) S  aA|bB; A  aA|a|b; B  bB|b|ε;

ж) S  aAc|bS; A  aA|Aa|ε;

з) S  aA|b; A  abA|abAcb; B  c;

и) S  aB|cA; A  BaA|a; B  A|a;

к) S  ABS|ε; A  abA|a; B  Ba|Bab|ε.

4.1.4. Является ли однозначной грамматика с правилами:

а) S  A|B; B  aB|b|C; A  AA|a; C  cC;

б) S  aAc|bS; A  aA|Aa|c;

в) S  aA|b; A  abA|abAcb; B  c;

г) S  aB|cA; A  BaA|a; B  A|b;

д) S  a|C; C  AB; A  aA|Ba|a; B  aB;

е) S  BA; A  Aa|bA|ε; B  Bb|aB|b;

ж) S  b|C; C  aC|AC; A  aA|Aa|a;

з) S  AB; A  aA|bA|a; B  Ba|Bb|ε.

4.1.5. Пусть G₁ - грамматика, имеющая продукции:

S  bA|ab; A  a|aS|bAA; B  b|bS|aBB;

а G₂ - грамматика, определяемая продукциями:

S  aB|aBS|bAS|bA; A  bAA|a; B  bBB|b.

Показать, что

1) G₁ - неоднозначная грамматика;

2) G₂ - однозначная грамматика;

3) L(G₁) = L(G₂):

4.1.6. Какой язык допускается автоматом с магазинной памятью

P = (Хq₀}, {a, b}, {z₀}, , q₀, z₀, {q₀}) ?

4.1.7. Построить МП-автоматы, определяющие языки

а) {ww^R : w  {a, b}^*};

б) язык всех цепочек из нулей и единиц с одинаковым числом

тех и других

в) {{a, b}^* {a^mbⁿa^mbⁿ} : m, n  1};

г) {{a, b}^* {a^mbⁿa^m} : m, n  1};

д) {{a, b}^* {ww} : w  {a, b]^*}:

4.1.8. Построить автомат с магазинной памятью, допускающий язык:

а) ({aⁿbⁿc^m|n, m  1})  ({a^mbⁿcⁿ|n, m  1});

б) {aⁿc^kbⁿ|k, n  1};

в) {a^mbⁿc^p|m + n + p  0(mod2), m, n, p  0};

г) {a^pb^qc^r|p + q > r;  p, q, r  0};

д) {x|x  {a, b}^*, |x|_a = |x|_b};

е) {x|x  {a, b}^*, |x|_a  |x|_b};

ж) {x|x  {a, b}^*; |x|_a = |x|_b, и для  u, v : x = uv; |u|  0, |v|  0 выполнено |u|_a > |u|_b}.

4.1.9. Пусть A - магазинный автомат. Построить магазинный автомат B, допускающий все префиксы языка

L(A), то есть язык

L(B) = {x|xy  L(A)}:

4.1.10. Построить детерминированные МП-автоматы, определяющие языки:

а) {wcw^R : w  {a, b}^*};

б) {0ⁿ1ⁿ : n  1}

в) {xcx^Rycy^R|x, y  {a, b}^*}.

4.1.11. Является ли язык L = {xcx^R|x (a*b*)*} детерминированным? Обосновать ответ с помощью магазинного автомата, допускающего язык L.

4.1.12. Является ли детерминированным следующий язык:

а) L = {x^Rcx|x  (a*b*)*};

б) L = {xcx^R|x  (b*a*)*};

в) L = {xcx^R|x  b*(a*)*}.

4.1.13. Доказать, что для любой КС-грамматики G' существует эквивалентная ей КС грамматика G, имеющая лишь правила вида

A  BC; A  a , где A, B, C  V_N; a  V_T .

4.1.14. Доказать, что если L₁ - КС-язык, то язык L, состоящий из всех слов L₁ четной длины - КС-язык, то есть

L = {X|X  L₁; |X| = 2K; K = 0, 1, ..., } - КС-язык.

4.1.15. Доказать, что для КС-грамматики G существует неукорачивающая КС-грамматика G', порождающая язык

L(G') = L(G) {ε}.

4.1.16. Привести алгоритм, позволяющий узнать, принадлежит ли данное слово данному КС-языку и доказать его правильность.

4.1.17. КС-грамматика называется левооднозначной, если каждое слово порождаемого ею языка имеет единственный левый вывод. Аналогично определяется правооднозначная грамматика. Построить пример левооднозначной, но не правооднозначной КС-грамматики.

C.4.2. Алгебраические свойства КС-языков. Лемма о разрастании.

4.2.1. Пусть L₁, L₂ - КС-языки. Докажите:

1) L₁  L₂ - КС-язык;

2) L₁L₂ - КС-язык.

4.2.2. Пусть L - КС-язык. Докажите:

1) L^* - КС-язык;

2) L^R - КС-язык.

4.2.3. Доказать, что не существует КС-грамматик, порождающих языки

а) {aⁿbⁿcⁿ} : n 1}; б) {ww : w {a, b}^*};

в) г) .

4.2.4. Выяснить, какие из приведенных ниже языков не являются КС-языками:

1) {aⁱb^jc^k|0  i <j< k};

2) {aⁱb^jc^k|0  i =j= k};

3) {aⁱb^jc^k|0  i = j, k  0, i   k};

4) {aⁱb^jc^k|0  i = j, k  0}:

4.2.5. Показать, что язык {aⁿbⁿcⁿ|n1g не является КС-языком.

4.2.6. Является ли язык {aⁿb^maⁿb^m|n 1, m 1} КС-языком?

4.2.7. Является ли язык {aⁿb^mbⁿa^m|n 1, m 1} КС-языком?

4.2.8. Является ли язык {a^p|p - простое число} КС- языком?

4.2.9. Является ли язык КС-языком?

4.2.10. Определить, замкнуто ли множество КС-языков относительно дополнения?

4.2.11. Замкнуто ли множество КС-языков относительно обращения? (Иначе говоря, верно ли, что если L - КС-язык, то L^R - тоже КС-язык).

Преобразования КС-грамматик

4.3.1. Указать множество бесполезных символов для грамматики:

S  A|B; B  aB|b|C; A  AA|a; C  cC:

4.3.2. Указать множество бесполезных символов в грамматике G = ({S, A, B, C}, {a, b, c}, P, S), где P состоит из

S  aSb|Abb|ε B  AB

A  aBCb|bAb C  a|c.

4.3.3. Указать множество бесполезных символов в грамматике G = ({S, A, B, C}, {a, b, c}, P, S), где P состоит из

S  A|B       A  aB|bS|b

B  AB|Ba     C  AS|b.

4.3.4. Указать множество бесполезных символов в грамматике G=({S, A, B, C, D}, {a, b, c}, P, S}, где P состоит из

S  aBb|aCb   A  Dc|cA

B  aS|b      C  AB|aD

D  AB|cDa.

4.3.5. Указать множество бесполезных символов в грамматике G = ({S, A, B, C}, {0, 1, 2}, P, S), где P состоит из

S  SS|A A  0A1|C|0

B  0C|1 C  BC|CS.

4.3.6. Являются ли следующие грамматики приведeнными? Указать для каждой грамматики множества недостижимых, бесплодных и бесполезных символов:

а) S  a|C    б) S  BA

 C  AB       A  Aa|bA|ε

 A  aA|Ba|a B  Bb|aB|b;

 B  aB;

в) S  b|C    г) S  AB

 C  aC|AC    A  aA|bA|a

 A  aA|Aa|a; B  Ba|Bb|ε;

д) S  A|B    е) S  aA|bB

 A  AA|a     A  aA|a|b

 B  aB|b|C   B  bB|b|ε;

 C  cC;

ж) S  aAc|bS з) S  aA|b

 A  aA|Aa|ε;  A  abA|abAcb

 B  c;

и) S  aB|cA к) S  ABS|ε

 A  BaA|a    A  abA|a

 B  A|a;     B  Ba|Bab|ε.

4.3.7. Построить приведeнные грамматики, эквивалентные следующим грамматикам:

a) S  A|B    A  C|D       B  D|E

C  S|a|ε     D  S|b       E  S|c|ε;

б) S  AB     A  Aa|bB     B  a|Sb.

4.3.8. Построить ε-свободные КС-грамматики, эквивалентные следующим грамматикам:

1) S  AB     2) S  ABC

A  C|ab      A  BB|ε

C  c|ε       B  CC|ε

B  aAa;      C  AA|b;

3) S  aSbS   4) S  AB

S  bSaS|ε;   A  SA|BB|bB

B  b|aA|ε.

4.3.9. Доказать, что для каждой КС-грамматики существует эквивалентная ей приведенная КС-грамматика.

4.3.10. Привести алгоритм построения множества достижимых символов и доказать его правильность

4.3.11. Доказать, что для каждой КС-грамматики существует эквивалентная ей КС-грамматика, не являющаяся леворекурсивной

Предсказывающий разбор сверху- вниз

4.4.1. Построить множества FIRST и FOLLOW для каждого нетерминала грамматики

а) S  aAB|B          б) S  aAB|BA

A  aA|a              A  BBB|a

B  BS|A|b;           B  AS|b;

в) S  S + T          г) S  ABC

S  T                 A  BB|ε

T  a                 B  CC|a

T  S[S];             C  AA|b;

д) S  aB|bA          е) S  Ba|Ab

A  aS|bAA|a          A  Sa|AAb|a

B  bS|aBB|b;         B  Sb|BBa|b;

ж) S  (SbS)          з) B  begin D; S end

S  (T)               B  s

S  a                 D  D; d

T  TS                        D  d

T  S;                        S  S; B

S  B;

и) A  aACd|b

C  c|ε.

4.4.2. Является ли следующая грамматика LL(1)? Использовать критерий LL(1).

S  aAb;      A  0;                A  aaA.

4.4.3. Для грамматики написать эквивалентную LL(1)- грамматику

а) S  aS|a;

б) S  ba|A           A  a|Aab|Ab;

в) S  aaS|abA                A  ε|Aa|Ab;

г) S  baaA|babA      A  ε|Aa|Ab;

д) S  abaA|abbA      A  ε|Aa|Ab;

е) S  ab|baA         A  ε|Aab|Ab.

4.4.4. Для следующих грамматик определить, являются ли они LL(k) грамматиками и найти точное значение k. Для LL(1)-грамматик построить детерминированный левый анализатор:

a) S  aAS|b          A  a|bSA;

б) S  A|B            A  aAb|0             B  aBbb|1;

в) S  ε|abA          A  Saa|b;

г) S  aS|a;

д) S  aAaa|bAba      A  b|ε;

е) S  Sa|b;

ж) S  TE';           E'  +TE'|ε           T  FT'

T'  *FT'|ε           F  (S)|a.

4.4.5. Определить, являются ли следующие грамматики LL(k)-грамматиками, и указать точное значение k:

а) S  Ab             A  Aa|a;

б)S  Ab              A  aA|a;

в) S  aAb            A  BB                B  ab|A|ε;

г) S  aAb            A  AaAb|ε;

д) S  aB             B  aBB|b.

4.4.6. Преобразовать грамматику к LL(1)-виду и построить для неe LL(1)-таблицу

а) S  Ab             A  aA|a;

б) S  aB             B  aBB|b:

4.4.7. Сколько тактов сделает LL(1)-анализатор для грамматики G c правилами:

S  aAB A  bC B  SS|ε C  A|ε

при разборе цепочки x = ab; ab, b ?

4.4.8. Является ли грамматика S Sa|b LL(2)- грамматикой?

4.4.9. Является ли язык, состоящий из всех целых чисел без знака и без незначащих нулей, LL(1)-языком?

4.4.10. Является ли язык, состоящий из всех цепочек из 0 и 1, не содержащих подцепочки 010, LL(1)-языком?

4.4.11. Является ли язык, состоящий из всех непустых цепочек из 0 и 1, не содержащих трех 1 подряд, LL(1)-языком?

4.4.12. Существует ли контекстно-свободная грамматика, LL(1)-таблица для которой не содержит элементов "ошибка" ?

4.4.13. Сформулируйте необходимые и достаточные условия того, что КС-грамматика есть LL(1)-грамматика. Докажите необходимость и достаточность.

Разбор снизу-вверх типа сдвиг- свертка

4.5.1. Построить все состояния для LR(0)-анализа грамматики G:

S  aAb;      A  ε;        A  aaA

Будет ли G LR(0)-грамматикой? А LR(1)?

4.5.2. Является ли грамматика с правилами:

S  A|B; B  aB|b|C; A  AA|a; C  cC

LR(0)-грамматикой?

4.5.3. Сколько множеств LR(0)-ситуаций в канонической системе LR(0)-ситуаций грамматики G с правилами

а) S  aA|aB          A  bA|c              B  bB|d;

б) S  A0|F1          A  S0|B1             B  A1|F0      F  B0|S1;

в) E  (L)|a          L  EL|E.

4.5.4. Сколько LR(0)-таблиц имеет грамматика с правилами:

S  Aa|Bb; B  b; A  ab.

4.5.5. Построить все состояния LR(1)-анализа для грамматики:

S  aAb; A  ε|aaA.

4.5.6. Сколько множеств LR(1)-ситуаций в канонической cистеме LR(1)-ситуаций грамматики G с правилами

а) S  aSb|ab;

б) S  aAc|b          A  aSc|b.

4.5.7. Определить, является ли грамматика c приведенным набором правил LR(1)-грамматикой:

а) A  aAB|b          B  b|ε;

б) S  SaS            S  a;

в) S  Abb|Bba                A  a         B  a;

г) S  aL|a           L  Lb|b.

4.5.8. Построить все состояния анализа (K = 1) для грамматики

S S₁; S₁S₁S₁; S₁a.

Будет ли эта грамматика LR(1)?

4.5.9. Построить все состояния LR(1) анализа для грамматики:

S  aBc;              B  b;                B  bBb:

Применив критерий LR(K), определить, будет ли это LR(1)- грамматика.

4.5.10. Выяснить, являются ли следующие грамматики LR(k)-грамматиками. Найти точное значение k и построить детерминированный правый анализатор:

а) S  SaSb|ε;

б) S  Sa|a;

в) S  C|d C  Ac|b D  aD|c;

г) S  Ab|Bc A  Aa|ε B  Ba|ε;

д) S  AB A  a B  CD|aE C  ab D  bb E  bba;

е) S  AB A  0A1|ε B  1B|1.

4.5.11. Является ли нижеприведенная грамматика LR(k), и если да, то определить минимальное k.

а) S  aAc    A  aSc       S  b A  b;

б) S  S1     S1  S1S1     S1  a;

в) S  aBc    B  b B  bBb;

г) S  aAc    S  b A  aSc       A  b;

д) S  aAb    A  0 A  aaA;

е) S  aAb    A  ε A  aaA.

4.5.12. Являются ли следующие грамматики LR(k)- грамматиками? Указать точное значение k и построить соответствующий детерминированный правый анализатор.

а) S  Ab     A  Aa|a;

б) S  Ab     A  aA|a;

в) S  aAb A  BB B  ab|A|ε;

г) S  aAb    A  AaAb|ε;

д) S  aB     B  aBB|b:

4.5.13. Для грамматики

S Ab|Bc A Aa|ε B Ba|ε

написать эквивалентную LR(0)-грамматику.

4.5.14. Сколько сверток и переносов сделает LR(1)- анализатор для грамматики G = ({S, A}, {a}, P, S) c правилами S A A Aa|a при анализе цепочки a100?

4.5.15. Сколько SLR(1)-таблиц имеет грамматика с правилами:

S  Aaa|Bb|C B  aa A  aa C  cAc|cBd.

4.5.16. Сколько тактов сделает LALR(1)-анализатор для грамматики с правилами:

S  A|BC B  a A  a; C  AAAS

при разборе цепочки aaaaa?

4.5.17. Выписать цепочку минимальной длины, на которой видны отличия LARL(1) и LR(1)-анализаторов для грамматики с правилами:

S  Aa|Bb|C B  aa A  aa C  cAc|cBd.

4.5.18. Пусть G = (N, T, P, S) - LR(1)-грамматика, w T^*. В каких случаях (в зависимости от G и w) LR(1)- анализатор при анализе цепочки w не сделает ни одного сдвига?

4.5.19. Пусть G = (N, T, P, S) - LR(1)-грамматика; w L(G); |w| = n: Пусть k - число сдвигов, делаемых LR(1)- анализатором при анализе цепочки w. Привести нижнюю и верхнюю оценку для числа k.

4.5.20. Пусть G = (N, T, P, S) - LR(1)-грамматика, |P| = m 1; w L(G), |w| = n. Пусть k - число сверток, делаемых LR(1)-анализатором при анализе цепочки w. Привести нижнюю оценку для числа k.

4.5.21. Пусть G = (N, T, P, S) - LR(1)-грамматика, |P| = m 1; w L(G), |w| = n. Пусть k - число сверток, делаемых LR(1)-анализатором при анализе цепочки w. Привести нижнюю оценку для числа k.

4.5.22. Существует ли LR(1)-грамматика, для которой функция действий LR(1)-таблицы не содержит элементов "ошибка" ?

4.5.23. Дана КС-грамматика G = (N, T, P, S). Найти верхнюю оценку числа LR(1)-ситуаций для G.

4.5.24. Дана LR(1)-грамматика без ε-правил G и цепочка w L(G). В дереве разбора w - n₁ листьев и n₂ внутренних вершин. Сколько сдвигов и сверток сделает LR(1)-анализатор для G при анализе цепочки w?

Элементы теории перевода

Атрибутные грамматики

5.3.1. Дополнить грамматику S 0S11; S 1S00; S ε до атрибутной так, чтобы вычислялась максимальная длина непрерывной последовательности единиц в порожденном слове.

5.3.2. Дополнить грамматику S AA; A 0A; A 1A; A ε до атрибутной так, чтобы вычислялась максимальная длина непрерывной последовательности из 1 в порожденном слове.

5.3.3. Дополнить грамматику S AA; A A0; A A1; A ε до атрибутной так, чтобы вычислялось число сочетаний 01 в порожденном слове.

5.3.4. В грамматике [целое] dC; C dC|ε терминал d имеет атрибут 0 или 1. Определить атрибуты так, чтобы нетерминал [целое] имел атрибут, равный восьмеричному значению выводимого числа.

5.3.5. Построить атрибутные грамматики для следующих переводов:

а) {(x, x)|x  {a, b}^*};               б) {(x, x^R)|x  {a, b}^*};

в) {(x, xx)|x  {a, b}^*};              г) {(aⁿbⁿ; aⁿbⁿcⁿ)|n  1}.

5.3.6. Привести пример атрибутной грамматики с некорректно заданными семантическими правилами

5.3.7. Привести пример атрибутной грамматики, вычисление атрибутов для которой нельзя выполнить параллельно с LL(1)-анализом.

5.3.8. Привести пример атрибутной грамматики, вычисление атрибутов для которой нельзя выполнить параллельно с LR(1)-анализом.

Генерация кода

Трансляция арифметических выражений

9.1.1. Для следующих арифметических выражений с помощью алгоритма Сети-Ульмана сгенерировать программу и изобразить атрибутированное дерево:

а) A*B + C*(D + E)*F;          б) A*(B + C)*(D + E)*F;

в) A + B + C*D + E*F;          г) A + B*C*D*E + F;

д) A + B*(C*D + E*F).

Трансляция логических выражений

9.2.1. Для следующих логических выражений сгенерировать код на командах перехода и изобразить атрибутированное дерево

а) A and not (B or C) or (D and E);

б) A and B and C or not (D or E);

в) A and (B or not (C and D) and E);

г) not (A and B or C or D) and E;

д) A and B or C or D and not E.

Люди также интересуются этой лекцией: Тема 12. ПРИЁМЫ ОКАЗАНИЯ ПЕРВОЙ ПОМОЩИ.

Генерация оптимального кода методами синтаксического анализа

9.3.1. Для следующих операторов присваивания сгенерировать оптимальный код методом сопоставления образцов:

а) a = b[i] + j;               б) a = b[i+5];                 в) a = b[i] + c[2];

г) a = b[i+2+j];               д) a = b[2+c[1]];              е) a = b[i+j];

ж) a = b[i+2] + 3;             з) a =j+ b[i+3];               и) a = b[i+j+1];

к) a = b[i+j] + 1.