Способы представление чисел в ЭВМ

Способы представление чисел в ЭВМ

Информация – это сведения об окружающем мире и протекающих в нем процессах, воспринимаемые человеком или специализированным устройством, например ЭВМ, для обеспечения целенаправленной деятельности.

Информация может быть числовой, текстовой, графической, звуковой, видео и т.д.

В ЭВМ используются две формы представления двоичных чисел:

- естественная форма или форма с фиксированной точкой (запятой);

- нормальная форма или форма с плавающей точкой (запятой).

Целые числа

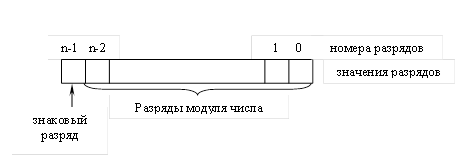
При решении задач целые числа встречаются в случаях представления индексов переменных, подсчета числа повторений каких-либо действий и т.д. Для хранения целых чисел в ячейке памяти предусматривается распределение разрядов (разрядная сетка) (рис. 1). Один из n разрядов отводится под знак числа, остальные разряды отводятся под модуль числа.

Рекомендуемые материалы

Рисунок 1 Разрядная сетка

Обычно применяют следующий способ кодирования знака числа: «+» обозначают цифрой 0, а «–» – цифрой 1 в знаковом разряде.

Модуль числа занимает в разрядной сетке ее младшие разряды, свободные старшие разряды заполняются нулями. Например, число –13₁₀, представленное в двоичной системе счисления значением –1101₂, в 8-разрядной сетке имеет вид, показанный на рисунке 2.

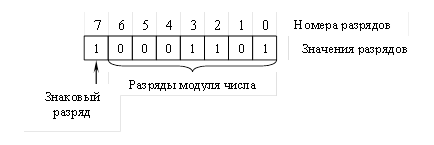
Рисунок 2 Запись числа –13, представленного в двоичной системе счисления,
в 8-разрядной сетке

Если количество значащих разрядов модуля числа превышает , происходит потеря старших разрядов модуля. Это явление, называемое переполнением разрядной сетки, приводит к ошибке в представлении числа.

Диапазон модулей чисел, которые могут быть представлены в n-разрядной сетке, от 0 (при цифре 0 во всех разрядах) до  (при цифре 1 во всех разрядах модуля).

В универсальных ЭВМ обычно используется два формата целых чисел: короткий – с числом разрядов  и длинный – с .

Числа с фиксированной точкой

У чисел с фиксированной точкой в двоичном формате предполагается строго определенное место точки. Обычно точка фиксируется перед старшим разрядом модуля числа (рис. 3).

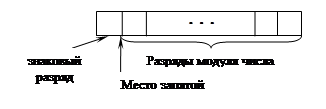
Рисунок 3 Запись числа с фиксированной точкой

Таким образом, значение модуля числа всегда оказывается меньше единицы.

При занесении числа в ячейку памяти свободные младшие разряды заполняются нулями, а если число значащих разрядов модуля больше , то младшие разряды модуля, которые не поместились в разрядной сетке, теряются. Если число имеет целую часть, то для ее хранения в разрядной сетке места нет, она теряется, число в разрядной сетке оказывается ошибочным.

Достоинство представления чисел в форме с фиксированной точкой состоит в простоте выполнения арифметических операций; недостатки – в низкой точности представления чисел с малыми значениями модуля (нули в старших разрядах модуля приводят к уменьшению количества разрядов, занимаемых значащей частью модуля числа).

Числа с плавающей точкой

Для научно-технических расчетов необходимо представлять числа в широком диапазоне и с достаточно большой точностью. Указанным требованиям отвечают числа с плавающей точкой (рис 4).

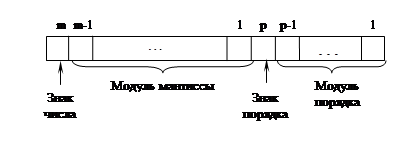
Рисунок 4 Запись числа с фиксированной точкой

Число состоит из мантиссы, старший разряд которой определяет знак числа, и порядка со знаком. Значение модуля мантиссы представляется двоичным дробным числом, т.е. запятая фиксируется перед старшим разрядом модуля мантиссы, порядок представляется целым числом. Порядок указывает действительное положение запятой в числе. В общем виде число с плавающей точкой записывается следующим образом:

,

где

Точность представления значений зависит от количества значащих цифр мантиссы. Для повышения точности числа с плавающей точкой представляют в нормализованной форме, при которой значение модуля мантиссы лежит в пределах . Признаком нормализованного числа служит наличие единицы в старшем разряде модуля мантиссы. В нормализованной форме могут быть представлены все числа из некоторого диапазона за исключением нуля.

В современных ЭВМ числа с плавающей точкой имеют основание системы счисления 16 и представляются в двух форматах: коротком (с числом разрядов 32) и длинном (с числом разрядов 64). Длинный формат предусматривает увеличение количества разрядов, отводимых в разрядной сетке под мантиссу, за счет чего повышается точность представления чисел.

Десятичные числа

Для кодирования десятичных чисел используются слова переменной длины с применением двух видов формата: упакованного и распакованного. Каждая десятичная цифра представляется двоичной тетрадой (двоично-десятичная система счисления) и занимает в разрядной сетке четыре разряда. Четыре разряда отводятся и для представления знака (собственно знак представляется младшим разрядом тетрады, в остальных разрядах тетрады может использоваться постоянная комбинация 110).

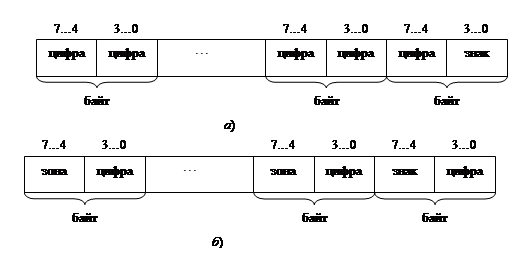
При использовании упакованного формата каждый байт (8 разрядов двоичного числа) содержит две десятичные цифры (рис 5,а).

В распакованном формате каждый байт содержит лишь одну десятичную цифру в младшей тетраде; старшая тетрада, называемая зоной, заполняется стандартной комбинацией 0011 (в соответствии с ASCII-кодом) (рис 5, б).

В лекции "Оглавление" также много полезной информации.

Рисунок 5 Структура поля а) упакованного формата
б) распакованного формата

Например, число  в ПК будет представлено:

- в упакованном формате:

0001               1001               0011               1101                                                                        

- в распакованном формате:

0011               0001               0011               1001               1101               0011