Способы описания сетей Петри
2.2. Способы описания сетей Петри
В настоящее время существует несколько подходов к описанию СП, которые можно разбить на следующие группы:
- матричное описание [26,46];
- алгебраическое описание [26,32];
- описание на основе базовых фрагментов;
- графическое описание.
Рассмотрим использование данных способов описания СП на примере ВС, состоящей из двух вычислительных устройств (ВУ), одно из которых главное (ВУ1), второе - подчиненное (ВУ2). Рабочий цикл ВУ складывается из трех этапов: начало работы (BEGIN), прием или посылка сообщений (INIT), окончание работы (END). На этапе BEGIN ВУ1 посылает устройству ВУ2 сигнал о начале работы и переходит в состояние ожидания ответа. ВУ2, получив сигнал о начале работы, переходит в активное состояние и выдает подтверждающее сообщение о готовности. ВУ1, получив подтверждающий сигнал, также переходит в активное состояние. На этом этап BEGIN заканчивается. Находясь в состоянии INIT , ВУ1 может либо передавать задания для выполнения устройству ВУ2, либо перейти в состояние END. В свою очередь ВУ2 может также передавать устройству ВУ1 задания для обработки, но самостоятельно в состояние END перейти не может. Если ВУ1 (ВУ2) передало задание устройству ВУ2 (ВУ1) для обработки, то оно переходит в состояние ожидания. Только после того, как будет получен подтверждающий сигнал, ВУ1 (ВУ2) может выполнить действия по инициализации новых заданий. Инициатива по переходу в состояние END может исходить только от ВУ1. При этом ВУ1 посылает устройству ВУ2 сигнал о завершении работы и переходит в неактивное состояние.
2.2.1. Матричное описание сетей Петри
Построим основанную на понятиях сетей Петри модель, которая описывает функционирование рассмотренной выше ВС. Подобные модели в дальнейшем будем называть СП-моделями. СП-модели системы ВУ1 и ВУ2 в соответствии с описанным выше примером представлены на рис.2.5. При этом позиции и переходы получили следующую интерпретацию.
Рекомендуемые материалы
Этап BEGIN:
p11 - ВУ1 находится в неактивном состоянии, но готово перейти в состояние BEGIN;
p14 - ВУ1 ожидает подтверждения о начале работы от ВУ2;
p15 - ВУ1 послало сигнал устройству ВУ2 о начале совместной работы;
p16 - ВУ1 получило подтверждающий сигнал от ВУ2 о начале совместной работы;
t11 - переход ВУ1 в состояние BEGIN;
N1 - действия ВУ2 при переходе в состояние BEGIN;
t12 - переход ВУ1 в состояние INIT;
p21 - ВУ2 находится в неактивном состоянии, но готово перейти в состояние BEGIN;
t21 - переход ВУ2 в состояние INIT.
Этап INIT:
p12 - ВУ1 готово послать сообщение устройству ВУ2;
p13 - ВУ1 готово принять сообщение от ВУ2;
p17 - ВУ1 ожидает подтверждения от ВУ2 о приеме сообщения;
p18 - ВУ1 послало устройству ВУ2 сообщение на обработку;
p19 - ВУ1 приняло от ВУ2 подтверждение о приеме посланного сообщения;
t13 - переход ВУ1 в состояние ожидания после передачи сообщения устройству ВУ2 на обработку;
t14 - переход ВУ1 в состояние готовности для передачи ВУ2 следующего сообщения;
N2 - действия ВУ2 при обработке принятого от ВУ1 сообщения;
p100 - ВУ1 обрабатывает принятое от ВУ2 сообщение;
 t15 - прием устройством ВУ1 сообщения от ВУ2;
t15 - прием устройством ВУ1 сообщения от ВУ2;
t16 - окончание обработки ВУ1 принятого от ВУ2 сообщения;
p22 - ВУ2 готово принять сообщение от ВУ1;
p23 - ВУ2 готово послать сообщение устройству ВУ1;
p24 - ВУ2 обрабатывает принятое от ВУ1 сообщение;
p25 - ВУ2 послало сообщение устройству ВУ1;
p26 - ВУ2 приняло от ВУ1 подтверждение о приеме посланного сообщения;
p27 - ВУ2 ожидает подтверждения от ВУ1 о приеме посланного сообщения;
t22 - прием ВУ2 сообщения от ВУ1;
t23 - окончание обработки ВУ2 принятого от ВУ1 сообщения;
t24 - переход ВУ2 в состояние ожидания после передачи сообщения устройству ВУ1 на обработку;
t25 - переход ВУ2 в состояние готовности для передачи устройству ВУ1 следующего сообщения;
N13 - действия ВУ1 при обработке принятого от ВУ2 сообщения.
Этап END:
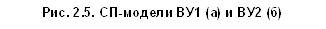
p101 - ВУ1 послало сообщение устройству ВУ2 об окончании совместной работы;
p102 - система ВУ завершила свою работу;
t17 - завершение работы ВУ1;
t26 - завершение работы ВУ2.
Матричное описание данных СП-моделей представлено на рис.2.6. Связь ВУ1 и ВУ2 в СП отображена наличием переходов N1, N2, N13. Использование ИСП позволяет исследовать работу ВУ1 (или ВУ2) независимо от ВУ2 (ВУ1). Если объединить СП, представленные на рис.2.5, то можно будет исследовать совместную работу ВУ1 и ВУ2.
Матрица F(p,t)
|
| t11 | N1 | t12 | t13 | N2 | t14 | t15 | t16 | t17 | t26 |
| p11 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| p14 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| p15 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| p16 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| p12 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 1 | 0 |
| p17 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 |
| p18 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 |
| p19 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 |
| p13 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 |
| p100 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 1 | 0 |
| p101 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 |
| p102 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 |
Матрица H(t,p)
| p11 | p14 | p15 | p16 | p12 | p17 | p18 | p19 | p13 | p100 | p101 | p102 | |
| t11 | 0 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| N1 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| t12 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 1 | 0 | 0 | 0 |
| t13 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 0 | 0 | 0 | 0 | 0 |
| N2 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 |
| t14 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| t15 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 |
| t16 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 |
| t17 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 |
| t26 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 |
Вектор начальной разметки m0
| p11 | p14 | p15 | p16 | p12 | p17 | p18 | p19 | p13 | p100 | p101 | p102 |
| 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |

 Матрица F(p,t) Матрица H(t,p)
Матрица F(p,t) Матрица H(t,p)
|
| t21 | t22 | t23 | t24 | t25 | N13 | t22 |
| p21 | 1 | 0 | 0 | 0 | 0 | 0 | 0 |
| p22 | 0 | 0 | 1 | 0 | 0 | 0 | 0 |
| p24 | 0 | 1 | 0 | 0 | 0 | 0 | 0 |
| p23 | 0 | 0 | 1 | 0 | 0 | 0 | 0 |
| p25 | 0 | 0 | 0 | 1 | 0 | 0 | 0 |
| p26 | 0 | 0 | 0 | 0 | 0 | 1 | 0 |
| p27 | 0 | 0 | 0 | 0 | 1 | 0 | 0 |
Вектор начальной разметки m0
| p21 | p22 | p24 | p23 | p25 | p26 | p27 |
| 1 | 0 | 0 | 0 | 0 | 0 | 0 |
б)
Рис. 2.6. Матричное описание СП-моделей ВУ1 и ВУ2
 Иногда бывает полезно отдельно изучить работу некоторого блока ВУ1 (или ВУ2). В этом случае исследуемый блок описывается как ИПР. В нашем примере ИПР N1, N2, N13, содержание которых представлено на рис.2.7, описывают работу блоков при переходе ВУ1 и ВУ2 в новое состояние и обработке принятых сообщений.
Иногда бывает полезно отдельно изучить работу некоторого блока ВУ1 (или ВУ2). В этом случае исследуемый блок описывается как ИПР. В нашем примере ИПР N1, N2, N13, содержание которых представлено на рис.2.7, описывают работу блоков при переходе ВУ1 и ВУ2 в новое состояние и обработке принятых сообщений.

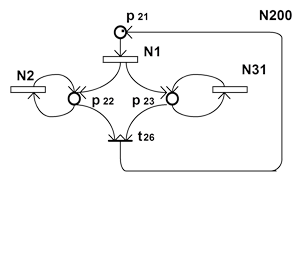 |
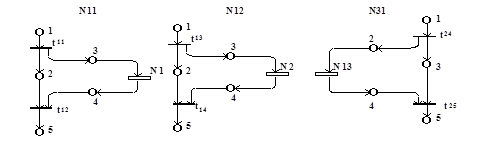
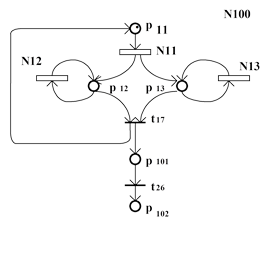 Для анализа взаимодействия отдельных блоков ВУ1 и ВУ2 на верхнем уровне ИСП, которые представлены на рис.2.5, могут быть описаны в виде, представленном на рис.2.8 и рис.2.9. Подобное представление абстрагируется от внутреннего содержания ИПР N1, N2, N11, N12, N13, N31, структура которых представлена на рис.2.7 и рис.2.10. Можно заметить, что данные ИПР включают в качестве составных частей другие ИПР (N1, N2, N13).
Для анализа взаимодействия отдельных блоков ВУ1 и ВУ2 на верхнем уровне ИСП, которые представлены на рис.2.5, могут быть описаны в виде, представленном на рис.2.8 и рис.2.9. Подобное представление абстрагируется от внутреннего содержания ИПР N1, N2, N11, N12, N13, N31, структура которых представлена на рис.2.7 и рис.2.10. Можно заметить, что данные ИПР включают в качестве составных частей другие ИПР (N1, N2, N13).  Приведенные примеры показывают, что применение ИСП дает возможность разработчику описывать и анализировать проектируемое устройство или систему на различных уровнях детализации.
Приведенные примеры показывают, что применение ИСП дает возможность разработчику описывать и анализировать проектируемое устройство или систему на различных уровнях детализации.

2.2.2. Алгебраическое описание сетей Петри
Одной из наиболее актуальных задач в области создания инструментальных средств для анализа и синтеза параллельных ВС является задача разработки средств формального описания СП, моделирующих работу исследуемой ВС. Основным требованием, предъявляемым к формальной модели, является адекватность представления моделей ВС, для которых характерны параллелизм, асинхронность, недетерминированное взаимодействие процессов. Кроме того, модель должна обладать развитым арсеналом средств, пригодных для исследования и преобразования моделей ВС. Существенную помощь в построении подобного математического аппарата может оказать алгебраический подход к описанию СП.
В настоящее время предложено несколько алгебраических подходов для описания как простых, так и расширенных СП [26,31,32,56]. В качестве примера подобного математического аппарата рассмотрим алгебру СП [30].
Алгебра сетей Петри базируется на алгебре регулярных СП [26]. В целях увеличения описательных возможностей языка в алгебру регулярных СП введены операции сцепления и замещения, средства описания межуровневых связей, ингибиторных и взвешенных дуг, а также расширены возможности операции присоединения.
Определение данных операций дается с помощью вспомогательной операции слияния позиций. Пусть X = {x1, x2,..., xn} и Y = {y1, y2, ..., ym} - два сливаемых множества позиций. Если одно из множеств пустое, то результат слияния представляет собой исходную сеть. Операция слияния sl множеств X и Y происходит в два этапа. Сначала каждая позиция xi, принадлежащая множеству Х, копируется в m экземплярах, а каждая позиция yj, принадлежащая множеству Y, копируется в n экземплярах. Позиции копируются вместе с их разметкой и инцидентными дугами. Затем каждая пара (xi, yj) замещается новой позицией z с разметкой m(z) = min(m(xi), m(yj)) и соответствующими инцидентными дугами. Рассмотрим определения операций алгебры регулярных СП.
Операция наложения “,”. Операция объединения двух сетей в одну выполняется путем наложения одноименных переходов:
N=(N1, N2)=(P1 È P2, T1 È T2, F1 È F2, H1 È H2, m0),
где m0(p)= m0i (p), если p Î Pi , где i=1,2 и p Î P1 Ç P2; m0(p) = min(m01(p), m02(p)), если p Î P1 Ç P2. Данная операция представляет собой теоретико-множественное объединение графов.
Операция итерации "*". Унарная операция, которая сливает множества головных и хвостовых позиций сети N :
N'=*(N)=sl(pre(N), post(N)).
Операция присоединения " ; ". Данная операция соединяет две сети в одну путем слияния множества хвостовых позиций первой сети N1 со множеством головных позиций второй сети N2 :
N=(N1; N2) = sl(post(N1), pre(N2)).
Операция исключения " $ ". Эта операция объединяет две сети в одну путем слияния соответствующих множеств головных и хвостовых позиций данных сетей:
N=(N1$N2) = sl(pre(N1), pre(N2))&sl(post(N1), post(N2)).
Операция разметки " > ". Унарная операция, помещает n меток в каждую позицию, принадлежащую множеству головных позиций сети N. Сеть N' совпадает как граф с сетью N, но имеет другую начальную разметку. Примеры использования описанных операций приведены на рис.2.11.
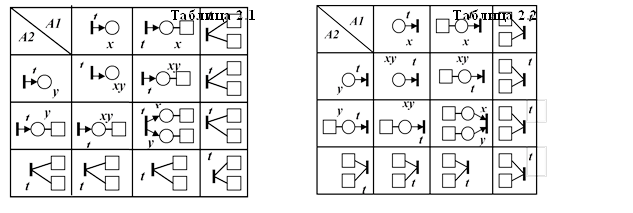 |
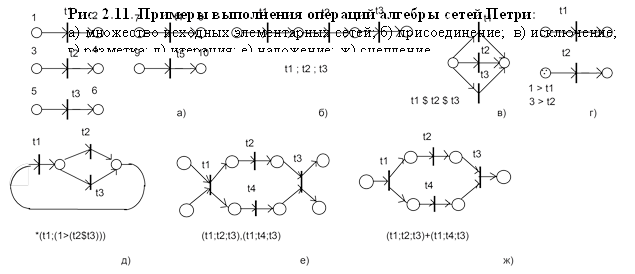
Операция сцепления " + ". Ввод данной операции обусловлен следующим. Ввиду того, что алгебраическое представление СП не включает идентификаторы позиций, при выполнении операции наложения учитываются лишь одноименные переходы. Это приводит к тому, что при наложении СП, представленных формулами, в некоторых случаях появляются непредусмотренные позиции, которые искажают результирующую сеть. Для устранения данного недостатка вводится операция сцепления, которая осуществляет наложение одноименных переходов сетей и производит сцепление позиций с определенными свойствами. Свойства объединяемых позиций x и y при сцеплении фрагментов СП А1 и А2, содержащих одноименный переход t, определяются таблицами 2.1 и 2.2.
Пример использования операции сцепления представлен на рис.2.11.
 Операция замещения " - ". На практике часто возникает ситуация, когда необходимо оценить влияние некоторого блока на работу ВС в зависимости от места включения блока. Например, на рис.2.12,а приведена СП-модель с идентификатором N100. Данная СП-модель описывает ВС, которая имеет последовательные и параллельные процессы. Пусть необходимо оценить работу ВС в том случае, когда блок Q10 (рис.2.12,б) включается вместо последовательного процесса (например, вместо t1, рис.2.13,а), и когда блок Q10 включается вместо параллельного процесса (например, вместо t4, рис.2.13,б). Как будет выглядеть алгебраическое описание СП-модели в первом и во втором случаях? Исходная СП-модель ВС и блок Q10 имеют следующее описание:
Операция замещения " - ". На практике часто возникает ситуация, когда необходимо оценить влияние некоторого блока на работу ВС в зависимости от места включения блока. Например, на рис.2.12,а приведена СП-модель с идентификатором N100. Данная СП-модель описывает ВС, которая имеет последовательные и параллельные процессы. Пусть необходимо оценить работу ВС в том случае, когда блок Q10 (рис.2.12,б) включается вместо последовательного процесса (например, вместо t1, рис.2.13,а), и когда блок Q10 включается вместо параллельного процесса (например, вместо t4, рис.2.13,б). Как будет выглядеть алгебраическое описание СП-модели в первом и во втором случаях? Исходная СП-модель ВС и блок Q10 имеют следующее описание:
N100:*(1>t1;(t4$(t2;t3));t5) , (2.3)
Q10:t21$t22$t23 . (2.4)
 ВС, в которой блок Q10 замещает последовательный процесс (t1), имеет следующее алгебраическое описание:
ВС, в которой блок Q10 замещает последовательный процесс (t1), имеет следующее алгебраическое описание:
N100:*(1>(t21$t22$t23);(t4$(t2;t3));t5),
а ВС, в которой Q10 замещает параллельный процесс (t4), имеет следующее описание:
N100:*(1>t1;((t2;t3)$(t21$t22$t23));t5) .
Очевидно, что подобный подход к алгебраическому представлению СП-моделей приводит к дублированию описания ИПР, а следовательно, к повышению сложности входного описания.
 Ликвидировать данный недостаток позволяет ввод дополнительной операции замещения. Правило записи данной операции имеет следующий вид: <П1>:<П2>-<П3> , где П1 - идентификатор СП-модели, в которой производится замещение; П2 - идентификатор замещающего ИП; П3 - идентификатор замещаемого перехода.
Ликвидировать данный недостаток позволяет ввод дополнительной операции замещения. Правило записи данной операции имеет следующий вид: <П1>:<П2>-<П3> , где П1 - идентификатор СП-модели, в которой производится замещение; П2 - идентификатор замещающего ИП; П3 - идентификатор замещаемого перехода.
 С учетом операции замещения СП-модели, представленные на рис.2.13, будут иметь следующие описания:
С учетом операции замещения СП-модели, представленные на рис.2.13, будут иметь следующие описания:
N100:Q10-t1 ,
N100:Q10-t4 ,
где N100 и Q10 - описаны выражениями (2.3) и (2.4).
Расширение операции присоединения. Операции алгебры регулярных СП [26] позволяют описывать ограниченные структуры СП. Так, например, с помощью операций данной алгебры нельзя описать фрагменты сетей, представленные на рис.2.14. А если принять во внимание то, что подобные структуры встречаются в большинстве СП-моделей, то становится очевидным ограниченность операций алгебры регулярных СП при описании и исследовании СП-моделей.
Пусть выполняется операция А1; А2 , где ";" - операция присоединения. Если фрагмент А1 имеет хвостовые позиции, т.е. |post(A1)| > 0 , а фрагмент А2 имеет головные позиции, т.е. |pre(A2)| > 0, то в этом случае операция присоединения выполняется, как описано выше.
 Рассмотрим случай, когда фрагмент А2 не имеет головных позиций (|pre(А2)|=0), либо фрагмент А1 не имеет хвостовых позиций (|post(A1)| = 0 ). Тогда, при выполнении операции присоединения для фрагментов А1 и А2 определяются позиции, которые входят в петли. Позиция р входит в петлю, если она принадлежит множеству pre(pre(p)) (либо множеству post(post(p))).
Рассмотрим случай, когда фрагмент А2 не имеет головных позиций (|pre(А2)|=0), либо фрагмент А1 не имеет хвостовых позиций (|post(A1)| = 0 ). Тогда, при выполнении операции присоединения для фрагментов А1 и А2 определяются позиции, которые входят в петли. Позиция р входит в петлю, если она принадлежит множеству pre(pre(p)) (либо множеству post(post(p))).
 Рассмотрим возможные варианты.
Рассмотрим возможные варианты.
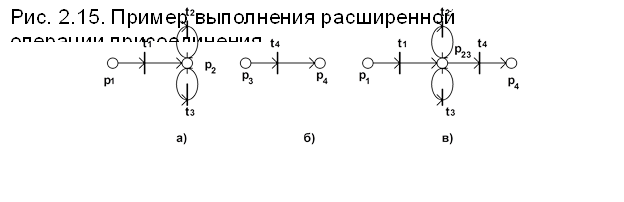
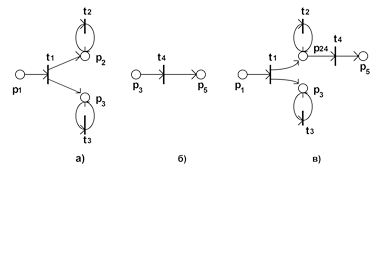
1. Если фрагмент А1 (рис.2.15,а) содержит одну позицию, входящую в петлю или петли, то операция присоединения (А1;А2) выполняется путем объединения данной позиции и головной позиции фрагмента А2 (рис.2.15,б). Результат данной операции представлен на рис.2.15,в.
2. Если фрагмент А3 (рис.2.16,а) содержит несколько позиций, причем часть из них входит в петли, то операция присоединения (А3;А2) выполняется путем объединения головной позиции фрагмента А2 с позицией фрагмента А3, входящей в одну из петель и имеющей наименьший порядковый номер. Результат данной операции представлен на рис.2.16,в.
3. В том случае, когда фрагмент А1 не имеет хвостовых позиций, а фрагмент А2 не имеет головных позиций, |post(A1)| = 0 & |pre(A2)| = 0 , то операция присоединения (А1;А2) невыполнима.
 Описание межуровневых связей. Для описания в СП-моделях межуровневых связей введем в алгебру сетей Петри составные имена переходов [27]. Рассмотрим использование данных имен на примере. Пусть в СП-модели (рис.2.17) существует связь между переходами, которые принадлежат различным ИПР. Тогда с использованием составных имен данная связь может быть описана следующим образом:
Описание межуровневых связей. Для описания в СП-моделях межуровневых связей введем в алгебру сетей Петри составные имена переходов [27]. Рассмотрим использование данных имен на примере. Пусть в СП-модели (рис.2.17) существует связь между переходами, которые принадлежат различным ИПР. Тогда с использованием составных имен данная связь может быть описана следующим образом:
 N1:(Q1,Q2)+(tQ1.12;tQ2.21) ,
N1:(Q1,Q2)+(tQ1.12;tQ2.21) ,
где - Q1:t11$t12 и Q2:t21;t22 .
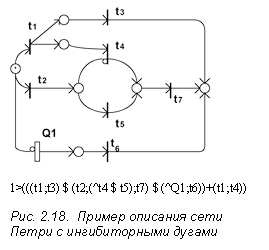
Описание ингибиторных дуг. Для алгебраического описания ингибиторных СП введем операцию задания ингибиторных дуг (^). Действие данной операции распространяется на один аргумент (унарная операция), в качестве которого может быть либо простой, либо иерархический переходы. Пример описания ингибиторной иерархической сети приведен на рис.2.18.
 Описание взвешенных дуг. Для того, чтобы иметь возможность описывать кратные дуги, встречающиеся в СП-моделях, вводятся операции задания весов входных и выходных дуг к переходам. Входная дуга к переходу ti кратности r описывается с помощью оператора g (rg(ti)), выходная - с помощью оператора h(rh(ti)). Например, дуги СП, представленной на рис.2.19, могут быть описаны следующим образом: 2gt1, 3ht1 или 2g3ht1 .
Описание взвешенных дуг. Для того, чтобы иметь возможность описывать кратные дуги, встречающиеся в СП-моделях, вводятся операции задания весов входных и выходных дуг к переходам. Входная дуга к переходу ti кратности r описывается с помощью оператора g (rg(ti)), выходная - с помощью оператора h(rh(ti)). Например, дуги СП, представленной на рис.2.19, могут быть описаны следующим образом: 2gt1, 3ht1 или 2g3ht1 .
Язык алгебраического описания иерархических сетей Петри
Возможности алгебраического описания представляются входным языком СП [30], в основу которого положена алгебра СП. Предложения языка СП включают только идентификаторы переходов и выполняемых над ними операций. Идентификаторы позиций генерируются в процессе интерпрeтации предложений языка СП и являются величинами переменными.
Алфавит языка включает следующие классы символов:
буквы: N,T,Q;
специальные знаки: ";",":",",","$","+","*","-",">",".","#', "(", ")", "g", "h", "^";
цифры: 0,1,2,3,4,5,6,7,8,9;
пробел.
Грамматика языка СП представлена на рис.2.20. Длина идентификаторов сети, ИПР и простых переходов (ПП) не должна превышать шести позиций. Причем каждый идентификатор должен начинаться с буквы. Каждый ИПР в терминах языка СП может быть описан либо как ИПР Q-типа, либо как ИПР N-типа. Использование того или иного типа ИПР позволяет влиять на степень детализации ИСП при ее анализе. В качестве примера опишем на языке СП СП-модель системы вычислительных устройств, которая представлена на рис.2.5. Одно из возможных описаний СП-модели можно представить следующим образом:
N0:*t0 (2.5)
Q11:(t11;t12)+(t11;t21;t12) (2.6)
Q2:t22;t23 (2.7)
Q12:(t13;t14)+(t13;Q2;t14) (2.8)
 Q13:t15;t16 (2.9)
Q13:t15;t16 (2.9)
Q31:(t24;t25)+(t24;Q13;t25) (2.10)
Q100:*(1>Q11;(*N12);t17)+(Q11;(*N13);t17;t26) (2.11)
Q200:*(1>t21;(*N2);t26)+(t21;(*N31);t26) (2.12)
 Q100:Q12-N12 (2.13)
Q100:Q12-N12 (2.13)
Q100:Q13-N13 (2.14)
Q200:Q2-N2 (2.15)
Q200:Q31-N31 (2.16)
N1:Q100+Q200 # (2.17)
 |
Поясним данное описание. Выражение (2.5) не несет физического смысла и присутствует в описании СП-модели только из-за требований грамматики языка. Ввиду того, что ИПР N1 состоит из одного перехода t21, то в алгебраическом описании данный переход замещен простым переходом t21. Иерархические переходы N2 и N13 описаны выражениями (2.7) и (2.9) и представлены как ИПР Q-типа. Данный подход выбран с целью наиболее полного раскрытия моделирующей СП. Выражения (2.6), (2.8), (2.10) описывают взаимодействие ВУ1 и ВУ2 на этапах BEGIN и INIT. Данные выражения описывают отдельные подсистемы и соответствуют структурному подходу к проектированию сложных систем. Выражения (2.11) и (2.12) описывают иерархические СП, моделирующие работу ВУ1 и ВУ2. Выражения (2.13)-(2.16) путем замены ИПР N-типа на ИПР Q-типа повышают уровень детализации СП-модели и делают ее более подробной. Полное описание моделирующей сети N1, в которой не содержится ни одного ИПР, получается в результате выполнения операции (2.17).
Следует отметить, что рассмотренное описание ИСП N1 не является оптимальным с точки зрения времени выполнения. Действительно, в выражении (2.11) ИПР Q11 включен дважды, поэтому при выполнении операции сцепления будут просматриваться и объединяться все переходы, составляющие ИПР Q11, что может занимать лишнее время в случае сложного Q11. Точно такого же результата, но значительно быстрее, можно добиться, если некоторые выражения представить в следующем виде:
Q11:(t11;t12)+(t11;t21;t12) (2.6)
Q100:*(1>N11;(*N12);t17)+(N11;(*N13);t17;t26) (2.11)
Q100:Q11-N11 (**)
N1:Q100+Q200 # (2.13)
В этом случае при выполнении операции сцепления в выражении (2.11) ИПР N11 не раскрывается и выступает в роли простого перехода. Поэтому ИПР Q100, описанный выражением (2.11), строится значительно быстрее, так как содержит меньшее количество переходов. После обработки выражения (**) в ИПР Q100 происходит замена ИПР N11 на ИПР Q11, в результате чего получается результат, аналогичный предыдущему описанию.
2.2.3.Описание сетей Петри на основе базовых фрагментов
Введем некоторые определения.
Определение 2.3. Базовой вершиной-переходом vt СП N , где t Î T, назовем фрагмент СП, включающий переход t и все позиции, для которых I(p,t) >=1 и O(p,t)>=1 .
Определение 2.4. Базовой вершиной-позицией vp СП N , где p Î P, назовем фрагмент СП, включающий позицию p и все переходы, для которых I(p,t) >=1 и O(p,t) >=1 .
Вершину-переход (vt) и вершину-позицию (vp) в дальнейшем будем называть базовыми фрагментами. Рассмотрим следующую теорему.
Теорема 2.1. СП N = (P, T, I, O, m0) считается заданной, если заданы множества P, T и отображение Г , которое может быть определено одним из следующих способов:
1) множеством вершин-переходов;
2) множеством вершин-позиций;
3) множествами входных элементов для каждой вершины:
Г={pre(bi)}, где bi Î P È T и i =  ;
;
4) множествами выходных элементов для каждой вершины:
Г={post(bi)}, где bi Î P È T и i =  .
.
В качестве примера рассмотрим задание СП-модели ВУ1, которая представлена на рис.2.5, с помощью базовых фрагментов.
1. Описание СП множеством вершин-переходов:
а) P={p11, p12, p13, p14, p15, p16, p17, p18, p19, p100, p101, p102};
б) T={t11, t12, N1, t13, t14, N2, t15, t16, t17, t26};
в) Г(t11)={p11},{p14, p15}, Г(t12)={p14, p16},{p12, p13},
Г(N1)={p15},{p16}, Г(t13)={p12},{p17, p18},
Г(t14)={p17, p19},{p12}, Г(N2)={p18},{p19},
Г(t15)={p13},{p100}, Г(t16)={p100},{p13},
Г(t17)={p12, p13},{p11, p101}, Г(t26)={p101},{p102};
г) m0 = (1 0 0 0 0 0 0 0 0 0 0 0).
2. Описание СП множеством вершин-позиций
а) P={p11, p12, p13, p14, p15, p16, p17, p18, p19, p100, p101, p102};
б) T={t11, t12, N1, t13, t14, N2, t15, t16, t17, t26};
в) Г(p11)={t17},{t11}, Г(p12)={t12, t14},{t13, t17},
Г(p13)={t12, t16},{t15, t17}, Г(p14)={t11},{t12},
Г(p15)={t11},{N1}, Г(p16)={N1},{t12},
Г(p17)={t13},{t14}, Г(p18)={t13},{N2},
Г(p19)={N2},{t14}, Г(p100)={t15},{t16},
Г(p101)={t17},{t26}, Г(p102)={t26}, Æ ;
г) m0 = (1 0 0 0 0 0 0 0 0 0 0 0).
3.Описание СП множеством входных элементов для каждой вершины
а) P={p11, p12, p13, p14, p15, p16, p17, p18, p19, p100, p101, p102};
б) T={t11, t12, N1, t13, t14, N2, t15, t16, t17, t26};
в) Г(t11)={p11}, Г(p11)={t17},
Г(t12)={p14, p16}, Г(p12)={t12, t14},
Г(N1)={p15}, Г(p13)={t12, t16},
Г(t13)={p12}, Г(p14)={t11},
Г(t14)={p17, p19}, Г(p15)={t11},
Г(N2)={p18}, Г(p16)={N1},
Г(t15)={p13}, Г(p17)={t13},
Г(t16)={p100}, Г(p18)={t13},
Г(t17)={p12, p13}, Г(p19)={N2},
Г(t26)={p101}, Г(p100)={t15},
Г(p101)={t17},
Г(p102)={t26};
г) m0 =(1 0 0 0 0 0 0 0 0 0 0 0).
4. Описание СП множеством выходных элементов для каждой вершины
а) P={p11, p12, p13, p14, p15, p16, p17, p18, p19, p100, p101, p102};
б) T={t11, t12, N1, t13, t14, N2, t15, t16, t17, t26};
в) Г(t11)={p14, p15}, Г(p11)={t11},
Г(t12)={p12, p13}, Г(p12)={t13, t17},
Г(N1)={p16}, Г(p13)={t15, t17},
Г(t13)={p17, p18}, Г(p14)={t12},
Г(t14)={p12}, Г(p15)={N1},
Г(N2)={p19}, Г(p16)={t12},
Г(t15)={p100}, Г(p17)={t14},
Г(t16)={p13}, Г(p18)={N2},
Г(t17)={p11, p101}, Г(p19)={t14},
Г(t26)={p102}, Г(p100)={t16},
Г(p101)={t26},
Г(p102)= Æ ;
г) m0 = (1 0 0 0 0 0 0 0 0 0 0 0).
Сравнивая достоинства и недостатки рассмотренных способов описания СП, можно отметить следующее. Достоинствами матричного метода является:
1) наличие алгоритмов анализа, ориентированных на матричное представление СП [30,46];
2) простота описания СП-модели.
"44 Период расцвета схоластики" - тут тоже много полезного для Вас.
К недостаткам метода относятся:
1) громоздкость;
2) сложность представления СП-модели на различных уровнях детализации.
Алгебраическое описание свободно от недостатков матричного описания, но в свою очередь достаточно сложно для использования и требует для работы определенных навыков. Другим существенным недостатком описанного в данной работе способа алгебраического описания является его ограниченность, то есть невозможность описания произвольных СП.
Алгебраическое описание СП-моделей, предложенное в работе [26], позволяет описывать СП любой структуры, но при этом язык алгебраических выражений требует обращения как к переходам СП, так и к позициям. Описание СП на основе базовых фрагментов просто и компактно в использовании, дает возможность описывать СП любой сложности. Однако описание СП на основе базовых фрагментов дает определенные неудобства при исследовании ИСП.
Графическое описание СП удобно, предоставляет наглядные средства при вводе и редактировании как простых, так и ИСП, однако данное описание требует разработки достаточно сложных специальных пакетов программ.





















