Анализ дискретных линейных систем МПС

Использование математического описания в форме (18.1), (18.2) дает ряд преимуществ при исследовании дискретных систем с вычислительной точки зрения. В частности оно позволяет легко формализовать решения задач анализа и синтеза ИС.

Например, математическое описание (18.1), (18.2) может быть использовано для матричной z- передаточной функцией, устанавливающей связь между входными и выходными переменными. Найдем эту z- передаточную функцию.

Введем z- преобразование координат:

x(z)=Z{x[k]}, y(z)= Z{y[k]}, u(z)= Z{u[k]}.

Применяя z- преобразование к обеим частям уравнений (18.1), (18.2) получим:

откуда:

(zE-Ф)x =H u+zx(0);

x =(zE-Ф)^-1 Hu +(zE-Ф)^-1 zx(0);

y =c(zE-Ф)^-1 Hu +c(zE-Ф)^-1 zx(0)+Ru(z) =

=[ c(zE-Ф)^-1 H+R] u + c(zE-Ф)^-1 zx(0) (18.3)

Положив в (5.29) , получим зависимость:

y =[ c(zE-Ф)^-1 H+R] u ,

устанавливающую связь между операторными изображениями входа и выхода. Матрица z- передаточных функций, связывающая входные переменные u₁, u₂,... u_m с выходными переменными y₁, y₂,... y_r, определится соотношением:

Для системы с m- выходами и r- входами матричная ПФ имеет размерность rх m, причем W_ij(z) представляет собой z- ПФ от j- того входа к i- тому выходу.

Рассмотрим вычисление матричной ПФ. Основная трудность заключается в определении обратной матрицы (zE-Ф)^-1. Аналитическое выражение для ее вычисления имеет вид:

где - присоединенная (взаимная) матрица (напомним, что это транспонированная матрица алгебраических дополнений элементов исходной матрицы).

Из приведенной зависимости, в частности, видно, что det(zE-Ф) - входит в матрицу передаточных функций. Этот детерминант определяет характеристическое уравнение системы:

Det (zE-Ф)=0.

Корни этого уравнения являются собственными числами матрицы Ф.

Таким образом, матричная z- ПФ содержит в качестве своих полюсов собственные числа матрицы Ф.

Алгоритмы получения ПФ, основанные на использовании уравнений состояния, удобнее алгоритмов, построенных на формулах - преобразования. Использование ЭВМ в задачах исследования дискретных систем позволяет применить стандартные программы обращения матриц, что приводит к существенному снижению трудоемкости выполняемых вычислений.

Пример вычисления z-ПФ силовой системы привода:

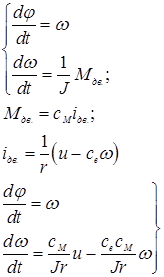
Введем обозначения:

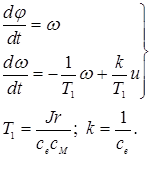
где - угол поворота вала двигателя;

- скорость;

u- управляющее напряжение;

k и T₁ - параметры ОУ.

Выберем вектор состояния . Тогда

Применим для вычисления переходной матрицы Ф - аналитический способ, основанный на использовании преобразования Лапласа.

при этом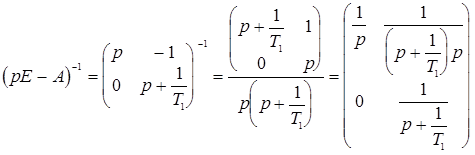

Найдем обратное преобразование:

(18.4)

Подставляя в (18.4) t=T (интервал квантования), получим переходную матрицу состояния дискретной системы:

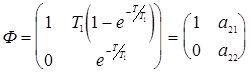
Перейдем к нахождению z- ПФ. Пусть y[k]=x[k], то есть e=E, R=0.

Тогда выражение для матричной ПФ примет вид:

Для определения элементов матрицы H найдем решение дифференциальных уравнений объекта при нулевых начальных условиях и u=1:

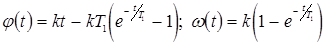
Подставив в полученные зависимости t=T, найдем матрицу H:

Матрица ПФ в данном случае характеризует связь напряжения u с координатами . Вычислим матрицу:

окончательно получим:

18.2. ИССЛЕДОВАНИ УСТОЙЧИВОСТИ ПРИ ОПИСАНИИ ДИСКРЕТНЫХ СИСТЕМ УРАВНЕНИЯМИ СОСТОЯНИЯ.

Устойчивость определяется характером собственных движений дискретной системы, то есть характером движений под действием только ненулевых начальных условий. Если входное воздействие отсутствует, то уравнение состояния (18.1) принимает вид:

x[k+1]=Ф x[k]. (18.5)

Общее решение системы (18.5) имеет вид:

x[k]=Ф^к x[0].

Устойчивость системы (18.5), а, следовательно, и исходной неоднородной системы (18.1) определяется, как это следует из предыдущего материала лекции, собственными числами матрицы Ф, то есть корнями характеристического уравнения:

det(zE-Ф)=0. (18.6)

Если все корни z_i, i=1,2,3,...,n удовлетворяют условию:

, i=1,2,3,...,n,

то система устойчива.

Если существует хотя бы один корень,

то импульсная система, описываемая уравнением (18.1), неустойчива.

При использовании математического описания импульсных систем в терминах пространства состояний оказывается возможным применить простой и удобный в вычислительном отношении критерий устойчивости.

Справедливы утверждения:

1. Если все корни характеристического уравнения (18.6) z_i(Ф) удовлетворяют условию

, i=1,2,3,...,n (18.7)

то . (18.8)

При этом в (18.8) может использоваться любая из известных форм нормы матрицы. Справедливо и обратное утверждение, то есть из условия (18.8) следует условие (18.7).

Пояснение:

Нормой матрицы А размера mхn называется сумма модулей ее элементов:

2. Если

, i=1,2,3,...,n (18.9)

и кратные корни на единичной окружности отсутствуют, то

(18.10)

и обратно, выполнение условия (5.36) влечет за собой выполнение (18.10).

3. Если существует или имеются кратные собственные числа матрицы Ф, принадлежащие единичной окружности, то

. Справедливо также и обратное утверждение.

Таким образом, исследование устойчивости может производиться на основе анализа элементов матрицы Ф^к при .

Обычно рассматривают последовательность матриц:

{Ф^2к}={Ф,Ф²,Ф⁴,...} .

Эта последовательность просто формируется с помощью ЭВМ. Далее задаются малым числом или достаточно большим числом N и с помощью ЦВМ проверяют выполнение одного из условий:

, к=0,1,2,...

или , к>n.

В первом случае соответствующая ИС устойчива, во втором - неустойчива.

Возможны модификации этого алгоритма на основе привлечения для оценки неустойчивости системы следов матриц Ф^к при .

При этом обычно используется следующее утверждение:

Если существует такое к, что SpФ^к> n, где n порядок матрицы, то среди собственных чисел матрицы обязательно найдется хотя бы одно z_i, удовлетворяющее условию и тогда соответствующая импульсная система неустойчива.

18.3.ВЫЧИСЛЕНИЕ ПЕРЕХОДНЫХ ПРОЦЕССОВ В ИС.

Перепишем уравнение (18.1) ИС в переменных состояния в виде:

x[k+1]=Фx[k]+Hu[k].

Это уравнение по существу представляет собой рекуррентное решение разностного уравнения дискретной системы, то есть оно позволяет определить вектор состояния x[k+1] по известным x[k] и u[k]. Поэтому данная форма уравнений позволяет рекуррентным способом вычислить переходные процессы и просто реализовать процесс вычислений на ЦВМ. Соответствующий алгоритм может быть использован и при переменных параметрах системы.

Недостатком рекуррентной процедуры является то, что для нахождения решения x[k] при определенном значении аргумента k необходимо вычисление решения при всех предшествующих значениях аргумента. Для получения решения x[k] в явном виде при произвольном значении аргумента может быть использован аппарат передаточных функций и z- преобразования.

Пояснения:

(Определения, которые были введены в курсе МОТАУ)

Допустим, задана однородная система уравнений:

х[k+1]=Фx[k] (18.11)

Тогда фундаментальной матрицей Х[k] называется (n x n) матрица, столбцы которой представляют собой линейно-независимые решения однородной системы конечно-разностных уравнений (КРУ).

Фундаментальная матрица является нормированной, если при k=0, Х[0]=Е.

В этом случае общее решение однородной системы будет иметь вид:

х[k]=X[k]x[0] . (18.12)

Для определения нормированной фундаментальной матрицы применим Z- преобразования к общим частям уравнения (5.38):

zx(z)-zx[0]=Фх(z),

где x(z)=z{x[k]}.

Отсюда следует:

x(z)=(zE-Ф)^-1zx[0]

и соответственно:

x[k]=Z^-1{(zE-Ф)^-1Z}x[0] . (18.13)

Так как решение линейного разностного уравнения при заданном начальном условии определяется единственным образом, то из сравнения выражений (5.38) и (18.13) будем иметь:

X[k]=Z^-1{(zE-Ф)^-1Z}.

Связь между Z- преобразованием решетчатой функции F(z) и оригиналом f[k] задается соотношением:

где z_i - особые точки F(z).

Применив эту формулу для нашего случая:

, (18.14)

где z_i- собственные числа матрицы Ф, то есть корни характеристического уравнения:

det(zE-Ф)=0.

Возможны также и некоторые другие способы вычисления матрицы Х[k].

Перейдем к определению решения неоднородной системы разностных уравнений:

х[k+1]=Фх[k]+Hu[k].

Получим последовательно:

х[1]=Фх[0]+Hu[0];

х[2]=Фх[1]+Hu[1]=Ф²х[0]+ФHu[0]+Hu[1];

х[3]=Фх[2]+Hu[2]=Ф³x[0]+Ф²х[0]+ФHu[1]+Hu[2];

Общее решение неоднородной системы будет иметь вид:

Вместе с этой лекцией читают "Дополнение 2".

х[k]=Ф^kx[0]+ Ф^k^-1Hu[0]+...+ФHu[k-2]+Hu[k-1]

или

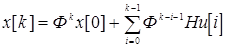
Учитывая, что: Ф^k=X[k], Ф^k^-ⁱ^-1=X[k-i-1], получим окончательное выражение в виде:

x[k]=X[k]x[0]+ . (18.15)

Таким образом, для численного расчета переходного процесса в дискретной системе можно использовать либо рекуррентную процедуру, либо выражения (18.13),(18.15). Последние выражения могут быть использованы для изучения общих свойств решения, анализа поведения системы при различных начальных условиях, так как они характеризуют зависимость переменных состояния системы от дискретного времени в явном виде.

Поделитесь ссылкой:

Популярные услуги

Анализ дискретных линейных систем МПС

Рекомендуемые материалы

Рекомендуемые лекции