Описание дискретных систем

Способ математического описания дискретных систем разностными уравнениями является наиболее общим и применяется как для линейных, так и для нелинейных систем. Разностные уравнения позволяют провести полное исследование системы, они хорошо приспособлены для решения задач анализа и синтеза с помощью ЭВМ.

Рассмотрим методику составления разностных уравнений импульсных систем на примере многомерной САУ. Уравнения для систем с одним выходом и одним входом являются частным случаем.

Итак, допустим, мы имеем многомерную синхронную, синфазную импульсную систему (рис.16.1).

Рис. 16.1.

Импульсные элементы в этой схеме имеют одинаковые частоты квантования и работают синфазно.

Пусть непрерывная часть системы описывается системой дифференциальных уравнений, которая в матричной форме записи имеет следующий вид:

где x=(x₁,x₂,...x_n)- n- мерный вектор переменных состояния;

u=(u₁,u₂,...u_m)- m- мерный вектор входных воздействий;

y=(y₁,y₂,...y_r)- r - мерный вектор выходных переменных.

Матрицы A,B,C,D имеют следующие размерности: А-(nхn)- матрица; B-(nхm)- матрица; C-(rхn)- матрица; D-(rхm)- матрица.

Двойные стрелки указывают на то, что устанавливаемые ими связи относятся к векторным величинам.

Матрица А - основная или собственная матрица системы. Она определяет устойчивость и, соответственно, характер свободных движений системы.

Матрица В - матрица формирования управления, она определяет передаточные свойства системы и характеристики вынужденного движения.

Матрица С- определяет связь между выходными переменными и переменными состояния.

Матрица D - устанавливает непосредственную зависимость выходных координат системы от входных переменных (так называемая матрица обхода).

Графически, уравнениям (16.1), (16.2) соответствует следующая структурная схема (рис.16.2):

Рис.16.2.

16.2. Переход от системы дифференциальных уравнений к системе конечно-разностных уравнений.

Рассмотрим решение однородной системы дифференциальных уравнений:

(16.3)

при начальных условиях : .

Общее решение:

x(t)=e^AtC₀,

где C₀- матрица - столбец, определяемая начальными условиями:

x(t₀)=x₀=e^At⁰C₀ ,

C₀=e^-At⁰x₀, x(t)=.

Пояснения:

- экспоненциальная матрица (nхn), определяемая как сумма ряда :

Экспоненциальная матрица обладает свойствами экспоненты:

1. t=0 , =E;

2. ;

3. .

Матрица:

Ф(t,t₀) = , (16.4)

определяющая решение однородного дифференциального уравнения, называется переходной матрицей состояния (матрицей перехода).

Свойства переходной матрицы:

1. Ф(t₀,t₀)=Е;

2. Ф(t,t₀)= Ф^-1(t₀ ,t);

3. Ф(t₀,t₂)= Ф(t₀,t₁) Ф(t₁,t₂), t₀< t₁< t₂;

4. Для линейной системы с постоянными коэффициентами матрица перехода является функцией только t-t₀ .

Теперь рассмотрим неоднородное уравнение:

. (16.5)

Обозначим

Ф(t,t₀)= =Ф(t-t₀).

Будем искать решение неоднородного уравнения (16.5) в виде:

x(t)=Ф(t-t₀)С₁(t) = С₁(t) . (16.6).

Дифференцируя (16.6) по t, получим:

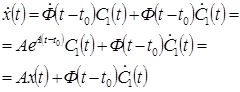
Сравнивая полученное уравнение и (16.5), получим:

Отсюда:

Учитывая, что

Далее, в соответствии со свойством переходной матрицы Ф(t₁,t₂)= Ф^-1(t₂ ,t₁), можно записать:

найдем произведение:

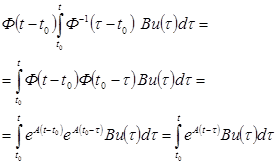
Таким образом, решение уравнения (16.5) можно записать в виде:

Матрицу- столбец С₂ найдем, используя начальные условия:

x(t₀)= С₂.

Окончательно получим:

Предположим, что в качестве формирующего звена используется экстраполятор нулевого порядка. Тогда в течение каждого из интервалов квантования: на вход непрерывной части поступает постоянный сигнал u(t)=const=u[kT]. Полагая известными значениями x при t₀=kT, найдем их значения при t=(k+1)T. Подставив соответствующие значения в решение системы дифференциальных уравнений, получим:

Окончательно уравнение состояния для дискретных моментов времени определится в виде:

x[(k+1)T]=Ф(T)x[kT]+Hu[kT], (16.7)

где

Дополняя уравнение (16.7) дискретным аналогом зависимости (16.2), получим окончательную систему разностных уравнений в виде:

x[(k+1)T]=Ф(T)x[kT]+H(Т)u[kT], (16.8)

y[kT]=Cx[kT]+Du[kT] (16.9)

где Ф - собственная матрица импульсной системы - Ф=е^АТ ;

Н- матрица входа:

; (16.10)

;

Е - единичная матрица соответствующей размерности . Матрицы С и D при переходе от уравнения (16.2 к (16.9) не изменяются .

Таким образом получена система разностных уравнений , описывающая ИС .

16.3. Некоторые численные способы вычисления переходной матрицы

Для вычислений переходной матрицы Ф=е^АТ применяют как аналитические , так и численные методы . Рассмотрим сначала аналитический метод , основанный на использовании преобразования Лапласа .

Выполним преобразования Лапласа над системой ДУ , описывающих

поведение САУ :

где ;

;

Сравнивая решение x(p)-в области изображения с решением x(t)-во временной области :

можно видеть ,что : .

Рассмотрим пример определения переходной матрицы.

Допустим задана система, поведение которой определяется следующей системой дифференциальных уравнений:

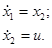
Решение:

Заданной системе соответствует структурная схема, приведенная на рис.16.3.

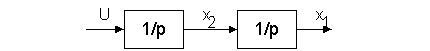
Рис.16.3.

Система дифференциальных уравнений в матричной форме записи:

Матрицы:

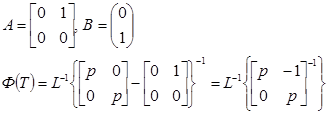
ПОЯСНЕНИЯ:

Обратная матрица:

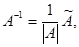
где - взаимная матрица, составленная из алгебраических дополнений транспонированной матрицы А^Т.

Алгебраическое дополнение: под алгебраическим дополнением элемента а_ijматрицы А понимают определитель матрицы, получаемый из исходной матрицы путем вычеркивания i- той строки и j- того столбца, взятый со знаком (-1)ⁱ⁺^j

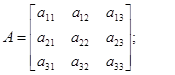
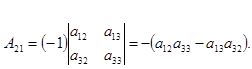
Вернемся к нашему примеру:

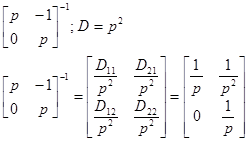
Находим обратные преобразования Лапласа от элементов матрицы:

Результат:

Существует ряд других аналитических методов нахождения переходной матрицы. Это методы, основанные на нахождении интерполяционного многочлена Лагранжа- Сильвестра и теоремы Кэли- Гамильтона. Однако все аналитические методы определения матрицы Ф отличаются сложностью и трудоемкостью, которые возрастают с увеличением размерности матрицы А.

Численные методы определения матрицы Ф=е^АТ основаны на вычислении суммы матричного степенного ряда:

где l определяет точность вычислений.

Недостаток вычислений матрицы Ф по такому алгоритму - возможная плохая сходимость степенного разложения, которая вместе с конечной разрядностью ЭВМ может привести к существенным погрешностям. Существенно лучшей сходимостью обладают алгоритмы, основанные на использовании степенных рядов, полученных в результате разложения по полиномам Чебышева. Они подробно рассмотрены в книге «Дискретные системы» под редакцией Ю.И. Топчеева.

16.4. Аналого – расчётный метод определения

параметров дискретной модели с использованием аналоговой

модели объекта управления.

Аналого-расчетный метод определения матриц системы конечно-разностных уравнений (КРУ), описывающей поведение объекта в дискретные моменты времени, предполагает известной аналоговую математическую модель объекта управления, описывающую ее поведение в непрерывном времени.

И так, предположим, что нам известна система дифференциальных уравнений, описывающая поведение объекта в непрерывном времени:

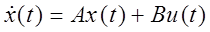
Требуется по известным параметрам модели (матрицам А и В) определить параметры дискретной модели (матрицы Ф и Н):

x[(k+1)T]=Ф(T)x[kT]+H(Т)u[kT],

Задача решается в два этапа.

1 Этап.

Определение матрицы Ф(Т).

Положим u[kT] = 0 , и рассмотрим решение однородной системы КРУ на первом такте квантования:

Возьмём вектор начальных условий в следующем виде :

Подставим х¹[0] в исходное уравнение, получим :

откуда, после преобразования будем иметь :

Таким образом, зная значение вектора состояния объекта управления на первом такте квантования можно определить первый столбец искомой переходной матрицы.

А как определить значения вектора состояния объекта управления? Для решения этой задачи можно воспользоваться аналоговой моделью объекта (рис.16.4). Задавая требуемые начальные значения вектора состояния x(0) и вектора управления, определяют решение по истечении времени t=T. Полученное решение и используется для определения соответствующего столбца переходной матрицы.

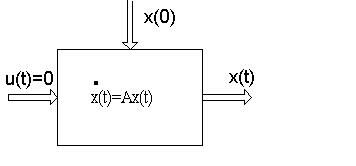
Рис.16.4.

В общем случае , для вектора начальных условий с нулевой координатой получим :

Таким образом, поскольку Ф(Т) есть матрица значений функций веса объекта от j – ого входа к i – ому выходу для i,j = 1,2,...n в момент времени Т, то методика определения состоит в следующем :

1. Составляется модель объекта;

2. Устанавливаются начальные условия только по j – ой координате

(x_j0 ,j = 1,...,n);

3. Запускается модель на время t = Т;

4. Определяются значения всех выходных координат вектора состояния x(T) и определяется j – ый столбец матрицы Ф(Т) делением полученных значений выходных координат на величину начального условия по j – ой координате.

Проделав эти операции для различных j = 1,2,...,n получим полный набор функций веса матрицы Ф(Т).

2.Этап.

Теперь определим матрицу Н(Т). при этом вектор начальных условий х(0) положим равным нулю, тогда из основного уравнения получим :

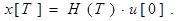
Производя преобразования аналогичные предыдущим, получим:

m-размерность вектора управления.

Процесс моделирования состояния системы в этом случае отображается следующей схемой (рис.16.5).

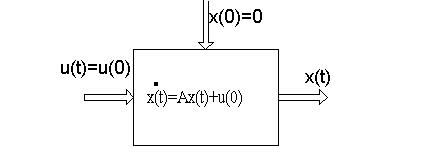
Рис.16.5.

Таким образом, для определения элементов матрицы Н(Т), необходимо :

1. На j – ый вход модели подать постоянный управляющий сигнал

u_j[0] ;

"59. Автоматические системы пожаротушения" - тут тоже много полезного для Вас.

2. Запустить модель на время t = Т ;

3. Замерить значения всех выходных координат и по последней формуле вычислить элементы j – ого столбца матрицы.

Проделав эти операции для j = 1,2,...,m, получим все элементы матрицы Н(Т).

Рассмотренный вариант определения матриц выгодно применить, когда заранее неизвестна величина периода дискретности T. В этом случае, записав функции веса и переходные функции объекта для достаточно большого интервала времени, можно определить набор матриц уравнения параметров состояния для различных периодов дискретности.

Определим также, что данный метод можно использовать для проверки правильности набора задачи на модели и ее исправности.

Данный метод определения матриц можно достаточно просто обобщить на случай переменных коэффициентов объекта, что выгодно отличает данный метод от ранее рассмотренных.

Поделитесь ссылкой:

Популярные услуги

Описание дискретных систем

Рекомендуемые материалы

Рекомендуемые лекции