Лекция 11 - Частотные критерии устойчивости
Лекция № 11
Тема:
Частотные критерии устойчивости импульсных систем.
План лекции:
1. Аналог критерия Михайлова.
2. Анализ устойчивости с помощью критерия Найквиста.
3. Анализ устойчивости импульсной системы с помощью ЛАФПЧХ.
.
1. Аналог критерия Михайлова.
Частотные критерии устойчивости удобно применять к системам высокого порядка. Одним из распространенных критериев устойчивости непрерывных систем является критерий Михайлова. Для импульсных систем можно сформулировать аналог этого критерия.
Пусть характеристическое уравнение замкнутой импульсной системы имеет вид
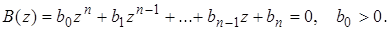
Рекомендуемые материалы
В соответствии с принципом аргумента [3] число корней характеристического многочлена, лежащих внутри единичной окружности, равно числу полных оборотов вектора 
при обходе точкой z единичной окружности, т.е.
.
Очевидно, что если m = n, то все корни 
удовлетворяют соотношению
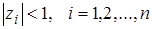
и система устойчива.
Наибольшую сложность при использовании этого критерия представляет нахождение отображения единичной окружности на плоскости B. При этом рассматривать многочлен B(z) в функции z неудобно, так как аргумент z меняется сложным образом. Проще перейти к переменной 
по формуле 
. При этом движению точки z по единичной окружности соответствует изменение в следующих пределах:
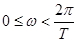
Таким образом, рассматривается функция 
и строится ее годограф в пределах 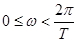. Так как имеет место соотношение
,
то годограф при изменении в пределах 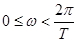симметричен относительно оси абсцисс. Отсюда следует, что можно рассматривать лишь полуветвь годографа, соответствующую половине исходного диапазона 
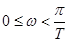. При этом приращение аргумента функции также уменьшится вдвое, т.е. 
;
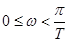
Примеры годографов, соответствующих устойчивым системам при n =1,2, 3, показаны на рис.25.
 |
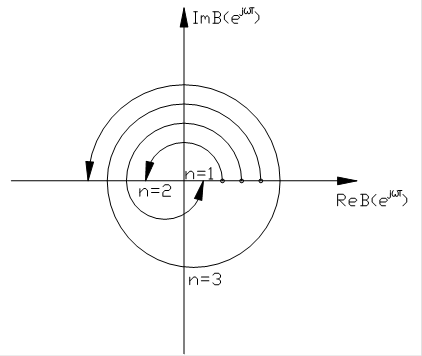Рис.25.
2. Анализ устойчивости с помощью критерия Найквиста.
Анализ устойчивости импульсных систем может быть выполнен также с помощью критерия Найквиста, который основан на использовании частотных характеристик разомкнутой системы. Рассмотрим простейшую схему замкнутой системы, представленную на рис.10. Пусть 
- частотная характеристика разомкнутой импульсной системы. Приведем формулировку критерия Найквиста без доказательства.
Пусть характеристическое уравнение разомкнутой импульсной системы имеет l корней вне единичного круга плоскости z. Для того, чтобы была устойчива замкнутая импульсная система, необходимо и достаточно, чтобы годограф при изменении w от 0 до 
охватывал точку 
) на комплексной плоскости W ровно l/2 раз, т.е.
,
.
Пусть разомкнутая система устойчива. Тогда годограф 1 на рис.26 соответствует системе, устойчивой в замкнутом состоянии, а годограф 2 - системе, неустойчивой в замкнутом виде.
 |
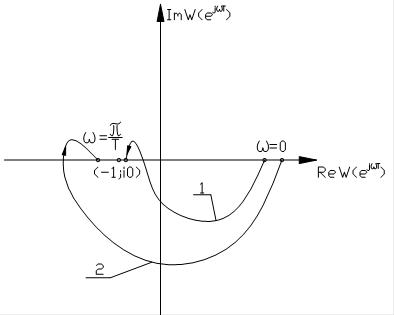Рис. 26
Случай, когда передаточная функция W(z) разомкнутой системы имеет полюса на единичной окружности плоскости z, относится к числу особых. В этом случае необходимо дополнить годограф частотной характеристики разомкнутой системы дугой бесконечного радиуса аналогично тому, как это делалось при исследовании непрерывных систем. Обычно полюсами, лежащими на единичной окружности, оказываются полюса z=1, что соответствует наличию полюсов p=0 (интегрирующих звеньев) в передаточной функции ПНЧ. При этом годограф АФЧХ разомкнутой системы дополняется дугой бесконечного радиуса, охватывающей столько квадрантов, каков порядок полюса z=1.
Пусть l=0 и разомкнутая система имеет полюс z=1 второго порядка. Годограф АФЧХ, представленный на рис.27а, соответствует системе, неустойчивой в замкнутом состоянии, на рис.27б - системе, устойчивой в замкнутом виде.
 |
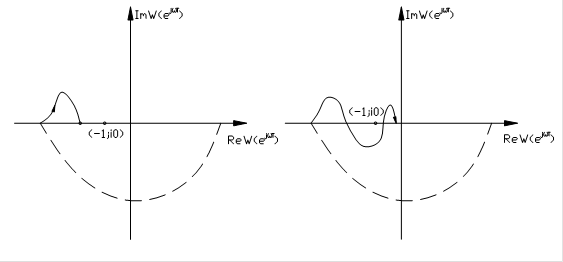Рис.27а Рис.27б.
3. Анализ устойчивости импульсной системы с помощью ЛАФПЧХ.
Для выполнения анализа устойчивости импульсной системы с помощью ее логарифмических ПНЧ, обратимся к простейшей структурной схеме замкнутой системы (см. рис.10) и рассмотрим, как должны выглядеть псевдочастотные ЛАФЧХ устойчивых и неустойчивых САУ. С формальной точки зрения критерий Найквиста для дискретных систем аналогичен критерию Найквиста для непрерывных систем [1] . Поэтому все рассуждения, связанные с формулировкой этого критерия в терминах ЛАФЧХ, могут быть перенесены и на дискретные системы. В частности, если разомкнутая импульсная САУ устойчива, то для устойчивости замкнутой системы необходимо и достаточно, чтобы в интервале псевдочастот, где ЛАФЧХ дискретной системы положительна, разность 
между числом положительных и отрицательных переходов ЛАФЧХ через линию 
равнялась нулю. При этом, как и ранее, положительным переходом считаем переход в сторону возрастания ЛАФЧХ, отрицательным - в сторону убывания ЛАФЧХ. Если передаточная функция разомкнутой системы имеет l полюсов вне единичного круга, то для устойчивости замкнутой системы необходимо и достаточно, чтобы в области положительности ЛАЧХ выполнялось условие
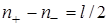
Псевдочастотные ЛАФЧХ системы, устойчивой в разомкнутом и замкнутом состояниях, показаны на рис.28, где 
.
Если передаточная функция разомкнутой системы имеет полюсы, лежащие на единичной окружности, то при соответствующих значениях аргумента ЛАЧХ системы стремится к бесконечности, а ЛАФЧХ изменяется скачком на величину 
, где r - порядок полюса.
 |
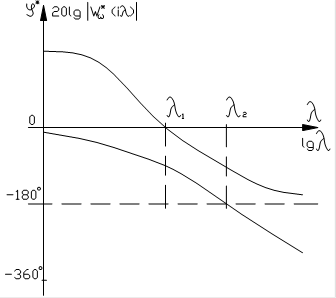Рис.28
Аналогичные особенности использования этого критерия характерны и для непрерывных САУ. Так как наиболее часто единичной окружности принадлежит полюс разомкнутой системы z=1 , то приведем окончательный результат для этого случая. Полюсу z=1 соответствуют w=l=0 . Так как при w=0 учитывается не вся величина скачка ЛАФЧХ , а только его половина, то при исследовании устойчивости для l=0 следует дополнить ЛАФЧХ скачком на 
, где r - порядок полюса z=1 .
Пусть, например Z -передаточная функция разомкнутой системы имеет полюс z=1 третьего порядка. АФЧХ и псевдочастотные ЛАФЧХ такой системы представлены на рис.29,а,б, где 
. Таким образом, замкнутая система будет устойчивой.
Пример. Оценим устойчивость замкнутой системы, структурная схема которой приведена на рис.30, где T=0.1 c, T1=0.2 c, k=2.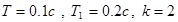
Передаточная функция такой системы была получена ранее. Она имеет вид
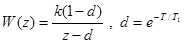
или в численном выражении
 |
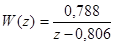
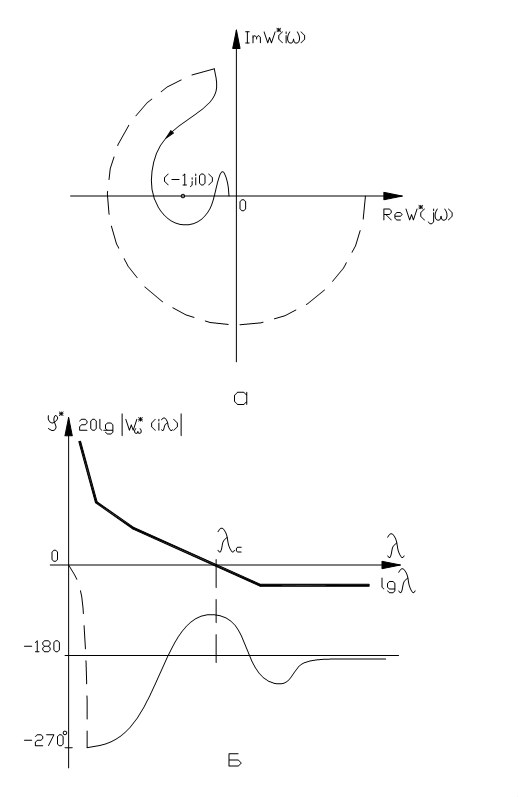Рис.29
Люди также интересуются этой лекцией: Общие процедуры MPI.
 |
Рис.30
Соответствующие псевдочастотные АФЧХ приведены на рис.31. Из их анализа можно заключить, что система является устойчивой. Увеличение коэффициента усиления может привести к возникновению неустойчивости системы.
Как и для непрерывных систем, для дискретных САУ можно ввести понятие запаса устойчивости по амплитуде и фазе (рис.32).
 |
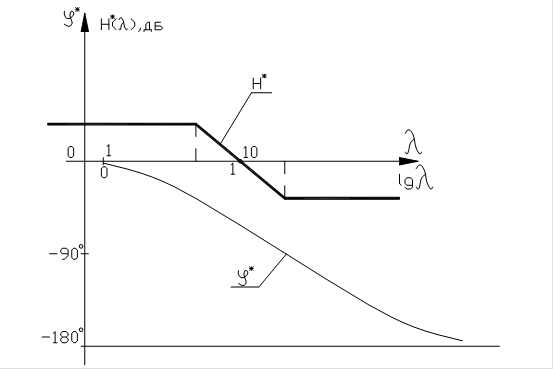Рис.31
Запас устойчивости по амплитуде показывает, во сколько раз можно увеличить коэффициент передачи разомкнутой системы без потери устойчивости, а запас устойчивости по фазе показывает, насколько можно увеличить величину дополнительного фазового запаздывания без потери устойчивости системы.
 |
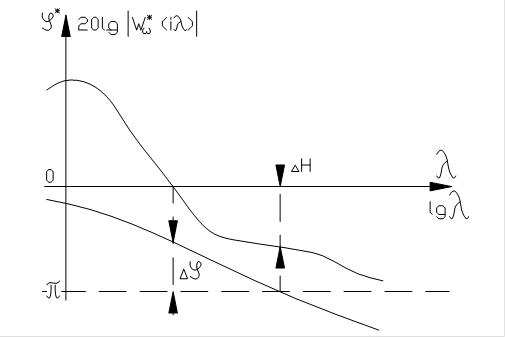Рис. 32
