Лекция 4

Принципы декомпозиции

Декомпозиция – это закрепление целей, задач, критериев их достижения и соответствующих числовых показателей за структурными элементами организации разного иерархического уровня. Были разработаны различные подходы декомпозиционных методов.

На этапе декомпозиции, обеспечивающем общее представление о решаемой проблеме, осуществляются:

· определение и декомпозиция общей цели исследования;

· выделение проблемы из среды, определение её ближнего и дальнего окружения;

· описание воздействующих факторов.

Наиболее часто декомпозиция проводится путём построения дерева целей и дерева функций. Основной проблемой при этом является соблюдение двух противоречивых принципов:

· полноты проблема должна быть рассмотрена максимально всесторонне и подробно;

· простоты — всё дерево должно быть максимально компактным «вширь» и «вглубь».

Рекомендуемые материалы

Компромисс достигается с помощью четырёх основополагающих понятий:

· существенности — в модель включаются только компоненты, существенные по отношению к целям анализа;

· элементарности — доведение декомпозиции до простого, понятного, реализуемого результата;

· постепенной детализации модели;

· итеративности — возможность введения новых элементов в основания и продолжение декомпозиции по ним на разных ветвях дерева.

Глубина декомпозиции ограничивается. Если при декомпозиции выясняется, что модель начинает описывать внутренний алгоритм функционирования элемента вместо закона его функционирования в виде «чёрного ящика», то в этом случае произошло изменение уровня абстракции. Это означает выход за пределы цели исследования системы и, следовательно, вызывает прекращение декомпозиции.

В современных методиках типичной является декомпозиция модели на глубину 5-6 уровней. На такую глубину декомпозируется обычно одна из подсистем. Функции, которые требуют такого уровня детализации, часто очень важны, и их детальное описание даёт ключ к основам работы всей системы.

В общей теории систем доказано, что большинство систем могут быть декомпозированы на базовые представления подсистем. К ним относят: последовательное (каскадное) соединение элементов, параллельное соединение элементов, соединение с помощью обратной связи.

Проблема проведения декомпозиции состоит в том, что в сложных системах отсутствует однозначное соответствие между законом функционирования подсистем и алгоритмом, его реализующим. Поэтому осуществляется формирование нескольких вариантов (или одного варианта, если система отображена в виде иерархической структуры) декомпозиции системы.

Наиболее часто применяемые стратегии декомпозиции:

· Функциональная декомпозиция. Декомпозиция базируется на анализе функций системы. При этом ставится вопрос, что делает система, независимо от того, как она работает. Основанием разбиения на функциональные подсистемы служит общность функций, выполняемых группами элементов.

· Декомпозиция по жизненному циклу. Признак выделения подсистем — изменение закона функционирования подсистем на разных этапах цикла существования системы «от рождения до гибели». Для жизненного цикла управления организационно-экономической системы выделяют этапы планирования, инициирования, координации, контроля, регулирования. Для информационных систем разделяют этапы обработки информации: регистрацию, сбор, передачу, обработку, отображение, хранение, защиту, уничтожение.

· Декомпозиция по физическому процессу. Признак выделения подсистем — шаги выполнения алгоритма функционирования подсистемы, стадии смены состояний. Хотя эта стратегия полезна при описании существующих процессов, результатом её часто может стать слишком последовательное описание системы, которое не будет в полной мере учитывать ограничения, диктуемые функциями друг другу. При этом может оказаться скрытой последовательность управления. Применять эту стратегию следует, только если целью модели является описание физического процесса как такового.

· Декомпозиция по подсистемам (структурная декомпозиция). Признак выделения подсистем — сильная связь между элементами по одному из типов отношений (связей), существующих в системе (информационных, логических, иерархических, энергетических и т. п.). Силу связи по информации можно оценить коэффициентом информационной взаимосвязи подсистем k= N/N0, где N — количество взаимоиспользуемых информационных массивов в подсистемах, N0 — общее количество информационных массивов. Для описания всей системы должна быть построена составная модель, объединяющая все отдельные модели. *

· Декомпозиция по входам для организационно-экономических систем. Признак выделения подсистем: источник воздействия на систему, это может быть вышестоящая или нижестоящая система, а также существенная среда.

· Декомпозиция по типам ресурсов, потребляемых системой. Формальный перечень типов ресурсов состоит из энергии, материи, времени и информации (для социальных систем добавляются кадры и финансы).

· Декомпозиция по конечным продуктам системы. Основанием могут служить различные виды продукта, производимые системой.

· Декомпозиция деятельности человека. Выделяется субъект деятельности; объект, на который направлена деятельность; средства, используемые в процессе деятельности; окружающая среда, все возможные связи между ними.

          Обычно декомпозиция осуществляется по нескольким основаниям, порядок их выбора зависит от квалификации и предпочтений системного аналитика.

Законы регулирования

1. П (пропорциональный) закон.

При этом законе управляющее воздействие u(t) пропорционально изменению отклонения Δ y =y*- u(t) (заданное минус фактическое).

U(t)=K_п  ∙ Δ y                   (1),

 где U(t) - управляющее воздействие;

k_п - коэффициент передачи, характеризует отклонение регулирующего воздействия к величине проблемы Δ y.

Переходная характеристика изображена на рисунке 1:

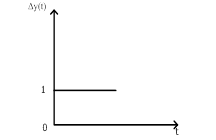
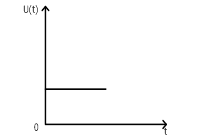
Рисунок 1 - Переходная характеристика. П закон.

Закон характеризуется мгновенной реакцией, которая не зависит от вида ∆y и определяется только величиной k_п.

Передаточная функция П – регулятора.

f _п (р) = k_п.                    (2).

Для дискретных систем закон преобразуется в разностную форму.

U_п(l) = k_п(l) · δy(l)                            (3)

                                   (4),

где t – непрерывное время;

∆T – шаг дискретизации.    

2. И (интегральный) закон.

Управляющие воздействия U(t) формируется на основе предыдущих воздействий в соответствии с возникновением отклонения от задания δy(t).

                       (5),

где Т_u -  постоянная времени интегрирования, характеризующая время анализа предыдущих управлений.

Переходная характеристика изображена на рисунке 2:

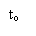
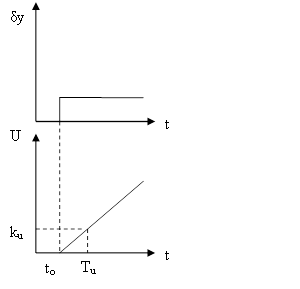
Рисунок 2 - Переходная характеристика. И закон.

Из-за времени Tu уменьшается быстродействие системы, однако по сравнению с П - законом отсутствует статистическая ошибка.

                          (6).

В дискретной форме данная функция имеет вид:

    (7).

Интегральный регулятор применяется для автоматических объектов не критичных к быстродействию.

3. ПИ (пропорционально - интегральный) закон.

Является комбинированным законом, тем самым оптимизируется процесс управления по быстродействию и качеству.

        (8).

Имеет два настроечных параметра k_п и Т_u позволяющих наиболее эффективно управлять процессом.

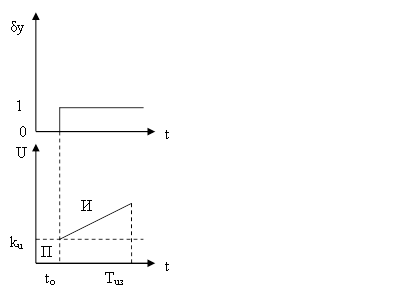
Рисунок 3 - Переходная характеристика. ПИ закон.

Сначала срабатывает быстродействующая часть – П – закон, максимально приближаясь к цели, остаток дорабатывается точностной И составляющей.

Передаточная функция будет иметь вид:

      (9).

Такая структура называется структурой с независимыми настройками. На практике часто применяется форма с зависимыми настройками:

         (10),

где   - время изодрома, характеризующее время выхода управляющего воздействия на величину 2 k_п.

Структура ПИ регулятора представлена на рисунке 4.

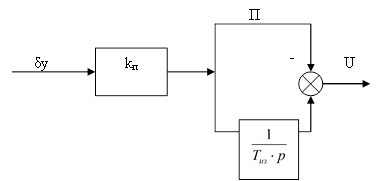
Рисунок 4 - Структура ПИ регулятора.

ПИ закон более распространен в системах управления.

4. ПД (пропорционально - дифференциальный) закон.

Управляющее воздействие U(t) пропорционально не только отклонению δy, но и скорости его изменения:

(11).

Здесь Т_д – постоянная времени дифференцирования, характеризующая время предвидения изменения δy.

Передаточная функция имеет вид:

                 (12).

По качеству регулирования соответствует П закону, но более сложен в реализации, поэтому на практике практически не применяется.

5. ПИД (пропорционально - дифференциальный) закон.

Включает в себя все три составляющие:

    (13).

Переходная характеристика будет иметь вид, представленный на рисунке 5.

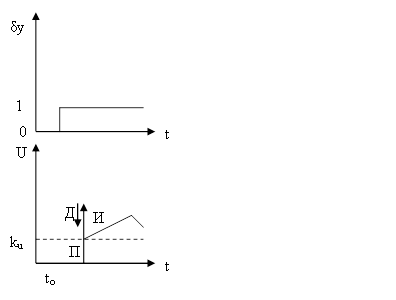
Рисунок 5 - Переходная характеристика. ПИД закон.

Сначала срабатывает прогноз (Д часть), после максимально достигая цели П часть, окончательная доработка цели И часть.

Передаточная функция имеет вид:

           (14).

На практике применяется формула:

(15),

где Т_п – время предвидения_, .

         Структура ПИ регулятора представлена на рисунке 6.

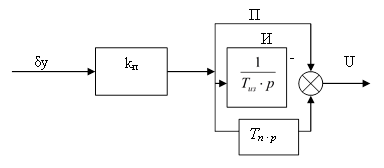
Рисунок 6 - Структура ПИД регулятора.

         ПИД регулятор является универсальным в плане настройки на любой закон управления, в дискретной форме имеет вид:

              (16).

                   (17).

Применяется в системах регулирования, которые требуют высокого качества и быстродействия.

Предпосылки для применения настроек по Ротачу

1) система должна быть линейна;

2) минимальная среднеквадратичная ошибка;

3) приведенная к выходу ошибка (возмущение) E(t) стационарная, случайная, с нулевым ожиданием и конечной дисперсией, этот процесс должен быть эргодическим;

4) автокорелляционная функция хорошо аппроксимируема экспоненциальной функцией;

5) высокая динамическая точность;

6) время запаздывания много меньше времени спада автокорреляционной функции;

7) возмущения представляют собой низкочастотный характер.

Данные условия практически никогда не соблюдаются, поэтому сначала производится настройка по Ротачу, а затем производится донастройка.

Настройка оценивания настроечных параметров по Ротачу

Применяется для систем регулирования с высокой предельной динамической точностью. При регулировании промышленных объектов обычно требуется, чтобы величина ошибки регулирования была существенно меньше отклонения регулируемой величины, которое имело бы место при отсутствии регулирования (не только автоматического, но и ручного). Применяемая к замкнутой системе формула для приближенного оператора регулятора:

,              (1)

где τ_μ – время запаздывания,

 - передаточная функция объекта регулирования без запаздывания

Выводится из формулы не приближенного оператора регулятора:

      (2),

где  - оператор оптимальной системы без учета запаздывания, причем дисперсия ошибки вычисляется как:

          (3),

где  - весовая характеристика формирующего фильтра.

Из формулы следует, что предельная точность ошибки регулирования системы зависит от статистических характеристик выходных воздействий и величины запаздывания в регулирующем канале. Так как система замкнута:

Ф(р) ≈ 1,

е^-τμр ≈ 1 - τ_μ · р               (4).

Путем подстановки условий 3 и 4 в формулу 2 получаем формулу 1.

В связи с трудностью вычислений произведем замену формулы 1 следующей формулой:

                  (5).

Система, описанная формулой 5 должна минимально отличаться от системы описанной формулой 1.

Последовательность решения задачи синтез реального регулятора в минимальной степени отличающегося от регулятора, который обеспечивает предельную динамическую точность регулирования:

1) исходя из общего вида характеристики  подбирается достаточно простая структура динамической характеристики , по формуле 5 рассчитывается соответствующая ей структура оператора регулятора (закон регулирования).

2) по характеристике объекта  и спектру мощности входного воздействия (х(t) – входное воздействие, G_хх(р) – спектр мощности) отыскиваются численные значения оптимальных коэффициентов оператора регулятора (параметры настройки регулятора), минимальную дисперсию ошибки регулирования σ_е².

Вам также может быть полезна лекция "25. Психологические аспекты конституции".

Причем дисперсия ошибки регулирования вычисляется по формуле:

                   (6).

Опыт показывает, что переходные характеристики для промышленных объектов имеют, как правило, не колебательный вид:

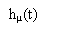
         Переходные характеристики промышленных объектов хорошо аппроксимируются инерционной системой 2-го порядка запаздывания.

.