Для студентов по предмету Теория вероятностей и математическая статистикаВ первой урне белых и черных шаров, во второй белых и черных. Из первой во вторую переложено К шаров, затем из второй урны извлечен один шарВ первой урне белых и черных шаров, во второй белых и черных. Из первой во вторую переложено К шаров, затем из второй урны извлечен один шар
2023-07-012023-07-01СтудИзба
В первой урне белых и черных шаров, во второй белых и черных. Из первой во вторую переложено К шаров, затем из второй урны извлечен один шар
Описание
Теория вероятностей и математическая статистика из задачника В.Ф. Чудесенко 2005 года, задача №13, вариант 31
В первой урне N1 белых и M1 черных шаров, во второй N2 белых и M2 черных. Из первой во вторую переложено К шаров, затем из второй урны извлечен один шар. Определить вероятность того, что выбранный из второй урны шар – белый.
![]()
В первой урне N1 белых и M1 черных шаров, во второй N2 белых и M2 черных. Из первой во вторую переложено К шаров, затем из второй урны извлечен один шар. Определить вероятность того, что выбранный из второй урны шар – белый.
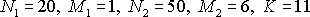
Характеристики решённой задачи
Номер задания
Вариант
Программы
Теги
Просмотров
0
Качество
Идеальное компьютерное
Размер
39,62 Kb
Список файлов
1688203372-43136-a26e77921758e29f74de8bf584fc4b0d.pdf
dmitry0376
01 июля 2023 в 12:22
![](https://s.studizba.com/z.php?f=/templates/si/i/noavatar.png&w=100&h=100&t=1"){kind=avatar}
