85541 (Возвратные задачи)

Федеральное агентство по образованию

Государственное образовательное учреждение высшего профессионального образования
Вятский государственный гуманитарный университет

Математический факультет

Кафедра алгебры и геометрии

Выпускная квалификационная работа

Возвратные задачи

Выполнила:

студентка V курса математического факультета

Ковязина Юлия Николаевна

Научный руководитель:

кандидат физико-математических наук, доцент кафедры алгебры и геометрии И.А.Семенова

Рецензент:

ст. преподаватель кафедры алгебры и геометрии

А.Н.Семенов

Допущена к защите в государственной аттестационной комиссии

«___» __________2005 г. Зав. Кафедрой Е.М. Вечтомов

«___»___________2005 г. Декан факультета В.И. Варанкина

Киров 2005

Содержание

Введение 3

Глава 1. 6

1.1 Задача о ханойской башне 6

1.2 Задача о разрезании пиццы 7

1.3 Задача Иосифа Флавия 10

Глава 2. Решение задач 19

Заключение 41

Библиографический список 42

Введение

Дискретная математика в настоящее время играет большую роль в разработке принципов работы компьютера, т.к. работа компьютера представляет собой выполнение последовательности дискретных шагов, приводящих к решению поставленной перед компьютером задачи.

Рассмотренная мною тема «Возвратные задачи» является небольшой частью дискретной математики, поэтому данная тема на сегодняшний момент является не менее актуальной.

Цель моей работы – изучить имеющийся теоретический и практический материал по данной теме и применить его к решению задач.

Данная работа состоит из введения, двух глав и заключения. Во введении приводятся примеры рекуррентных соотношений, с помощью которых можно задать некоторые последовательности, а так же рекуррентные соотношения, которые могут использоваться при решении задач. В первой главе описываются три задачи: задача о ханойской башне, задача о разрезании пиццы и задача Иосифа Флавия, а также доказываются некоторые факты, которые в литературе предлагаются для самостоятельного доказательства. Вторая глава посвящена решению задач на данную тему. В заключении делаются выводы о проделанной работе и указываются дальнейшие перспективы.

В основе решения возвратных задач лежит идея возвратности (или рекуррентности), согласно которой решение всей задачи зависит от решения той же самой задачи меньших размеров.

Тема «Возвратные последовательности» не является изолированной, нигде не используемой теорией. Наоборот, возвратные последовательности близки к школьному курсу математики (арифметическая и геометрическая прогрессии, последовательности квадратов и кубов натуральных чисел и т.д.), используются в высшей алгебре, геометрии, математическом анализе и других математических дисциплинах. Теория возвратных последовательностей составляет особую главу математической дисциплины, называемой исчислением конечных разностей; представляет собой частную главу о последовательностях.

Таким образом, возвратные последовательности являются настоящей маленькой теорией, законченной, простой, ясной.

Определение: Пусть имеется последовательность {u_n}:

u₁, u₂, u₃,…, u_n, … (1)

Если существует натуральное число k и числа a₁, a₂, a₃, …,a_k (действительные или мнимые) такие что, начиная с некоторого номера n и для всех следующих номеров

u_n+k=a₁∙u_n+k-1 + a₂∙u_n+k-2 +…+a_k∙u_n при n ≥ 1 (2)

то последовательность (1) называется возвратной последовательностью порядка k , а соотношение (2) – возвратным (рекуррентным) уравнением порядка k.

Таким образом, зная k первых членов последовательности можно определить всю последовательность, т.е. вычислить любой наперед заданный член последовательности.

С помощью рекуррентных соотношений можно задать следующие последовательности:

1). Геометрическая прогрессия

u_n+1 = q∙u_n

2). Арифметическая прогрессия

u_n+1 = u_n + d

другой вид u_n+2 = 2∙u_n+1 − u_n

3). Последовательность чисел Фиббоначи

u_n+2 = u_n+1 +u_n

4). Последовательность квадратов натуральных чисел

u_n+1 = u_n + 2∙n + 1

другой вид u_n+3 = 3∙u_n+2 − 3∙u_n+1 + u_n

5). Последовательность кубов натуральных чисел

u_n+4 = 4∙u_n+3 − 6∙u_n+2 +4∙u_n+1 − u_n

6). Все периодические последовательности: u₁, u₂, …, u_k+1, …

u_n+k = u_n.

Также рекуррентные соотношения могут использоваться при решении задач (в частности, при доказательстве равенств):

7). Интегрирование простейших рациональных дробей IV типа

Обозначим I_m= , где t = x+

I_m= ∙I_m-1

8). Интеграл I_n=

I_n= ∙I_n-2

9). Формула длины стороны при удвоении числа сторон правильного вписанного многоугольника

a_n= , при n ≥ 2

R – радиус описанной окружности

Если сторона a₁ исходного правильного вписанного многоугольника задана, то a_n есть сторона многоугольника, полученного из исходного (n-1) кратным удвоением числа сторон.

10). Дифференциальные уравнения высших порядков

y⁽ⁿ⁾ = f(x, y, y', y», …, y^(n-1))

11). Определитель Вандермонда

∆_n=∆(x₁, x₂, …, x_n)=

∆ (x₁, x₂, …, x_n) =(x_n −x₁)(x_n-1−x₁)…(x₂−x₁)∙∆(x₂, x₃, …,x_n).

Глава 1

1.1. Задача о ханойской башне

Рассмотрим сначала маленькую изящную головоломку под названием ханойская башня, которую придумал французский математик Эдуард Люка в 1883 г. Башня представляет собой восемь дисков, нанизанных в порядке уменьшения размеров на один из трех колышков. Задача состоит в том, чтобы переместить всю башню на один из других колышков, перенося каждый раз только один диск, и не помещая больший диск на меньший.

Будем решать эту задачу в общем виде, т.е. посмотрим, что будет в случае n дисков.

Будем говорить, что T_n есть минимальное число перекладываний, необходимых для перемещения n дисков с одного колышка на другой по правилам Люка.

Рассмотрим крайние случаи: Т₀=0, T₁=1, T₂=3, T₃=7. Эксперимент с тремя дисками дает ключ к общему правилу перемещения n дисков: сначала мы перемещаем (n−1) меньших дисков на любой из колышков (что требует Т_n-1 перекладываний), затем перекладываем самый большой диск (одно перекладывание ) и, наконец, помещаем (n−1) меньших дисков обратно на самый большой диск (еще Т_n-1 перекладываний). Таким образом, n дисков (при n>0) можно переместить самое большое за 2T_n-1+1 перекладываний (т.е. достаточно перекладываний): T_n ≤ 2T_n-1+1.

Сейчас покажем, что необходимо 2T_n-1+1 перекладываний. На некотором этапе мы обязаны переместить самый большой диск. Когда мы это делаем, (n−1) меньших дисков должны находиться на одном колышке, а для того чтобы собрать их вместе, потребуется по меньшей мере Т_n-1 перекладываний. Самый большой диск можно перекладывать и более одного раза. Но после перемещения самого большого диска в последний раз мы обязаны поместить (n−1) меньших дисков (которые опять должны находиться на одном колышке) обратно на наибольший диск, что также требует Т_n-1 перекладываний. Следовательно, T_n ≥ 2T_n-1+1.

Эти два неравенства вместе с тривиальным решением при n=0 дают рекуррентное соотношение:

(1)

Т₀=0

T_n = 2T_n-1+1 при n>0

При достаточно большом n для вычисления Т_n потребуется слишком много времени, поэтому получим Т_n в простой, компактной, «замкнутой форме», что позволит вычислить Т_n быстро.

Первый способ решения (угадывание правильного решения с последующим доказательством, что наша догадка верна).

Вычислим: Т₃=2∙3+1=7; Т₄=2∙7+1; Т₅=2∙15+1; Т₆=2∙31+1=63. Теперь можно сделать предположение, что

Т_n =2ⁿ − 1 при n≥0. (2)

Докажем методом математической индукции по числу n:

1. База: n=0, Т₀=2⁰–1=1–1=0 (верно);

2. Индуктивный переход: пусть доказано для всех чисел t ≤ (n–1). Докажем для t=n: Т_n= 2T_n-1+1 2(2^n-1−1)+1 = 2∙2^n-1−2+1 = 2ⁿ − 1

Из пунктов 1 и 2 следует: при n≥0 Т_n = 2ⁿ − 1

Второй способ решения.

К обеим частям соотношения (1) прибавим 1:

Т₀+1 = 1,

Т_n+1 = 2T_n-1+2 при n>0.

Обозначим U_n = T_n+1, тогда получим

U₀ = 1

U_n = 2U_n-1 при n>0.

Решением этой рекурсии есть U_n=2ⁿ; следовательно Т_n = 2ⁿ−1.

1.2. Задача о разрезании пиццы

Формулировка задачи: сколько кусков пиццы можно получить, делая n прямолинейных разрезов ножом? Или, каково максимальное число L_n областей, на которые плоскость делится n прямыми?

С

1

нова начнем с рассмотрения крайних случаев.

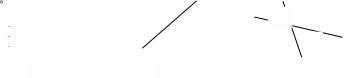
Эксперимент с тремя прямыми показывает, что добавленная третья прямая может рассекать самое большое три старых области вне зависимости от того, как расположены первые две прямые:

Т аким образом, L₃=4+3=7 – самое большое, что можно сделать.

Обобщая, приходим к следующему выводу: новая n-я прямая (при n>0) увеличивает число областей на k когда рассекает k старых областей когда пересекает прежние прямые в (k−1) различных местах. Две прямые могут пересекаться не более чем в одной точке. Поэтому новая прямая может пересекать (n−1) старых прямых не более чем в (n−1) различных точках, и мы должны иметь k ≤ n. Установлена верхняя граница:

L_n ≤ L_n-1+ n при n>0

В этой формуле можно достичь равенства следующим образом: проводим n-ю прямую так, чтобы она не была параллельна никакой другой прямой (следовательно, она пересекает каждую из них) и так, чтобы она не проходила ни через одну из имеющихся точек пересечения (следовательно, она пересекает каждую из прямых в различных местах). Поэтому рекуррентное соотношение имеет вид:

L₀ = 1

L_n = L_n-1+ n при n > 0

Теперь получим решение в замкнутой форме.

L_n = L_n-1+ n = L_n-2+ (n−1) + n = L_n-3+ (n−2) + (n−1) + n = … = L₀+ 1 + 2+ +… + (n−2) + (n−1) + n = 1 +

L_n = + 1 при n ≥ 0 (3)

Докажем полученное равенство методом математической индукции.

1. База: n=0, L₀= = 1 (верно);

2. Индуктивный переход: пусть доказано для всех чисел t ≤ (n–1). Докажем для t=n:

L_n = L_n-1+ n = =

Из пунктов 1 и 2 следует: при n ≥ 0 L_n = + 1

А

3

теперь небольшая вариация на тему прямых на плоскости: предположим, что вместо прямых линий мы используем ломаные линии, каждая из которых представлена одним «зигом». Каково максимальное число Z_n областей, на которые плоскость делится n такими ломаными линиями?

Ч

2

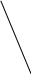
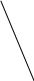астные случаи:

4

2

6

7

1

1