lektsia_9_2007_dlya_studentov_ON (Лекции по линейной алгебре АВТИ)

Лекция 9

Аналитическая геометрия. Векторная алгебра

1. Основные определения.

Линейные операции над векторами

Вектор – направленный отрезок, точка A – начало отрезка, точка В – конец отрезка:

A

B

Будем обозначать векторы :

Определение 1. Вектор является нулевым вектором, если точки A и B совпадают: .

Определение 2. Векторы называются коллинеарными, если, будучи приведены к общему началу, они лежат на одной прямой:

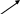
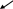
Нулевой вектор коллинеарен любому вектору.

Определение 3. Векторы называются компланарными векторами, если, будучи приведены к общему началу, они лежат в одной плоскости:

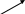
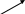
Определение 4. Длиной вектора называется длина отрезка AB: = AB.

Определение 5. Векторы называются равными, если

1. ;

2. направления векторов совпадают.

Определение 6. (суммы векторов)

Суммой векторов называется вектор (обозначается ), который строится либо по правилу параллелограмма, либо по правилу треугольника:

1. правило параллелограмма:

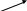
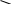
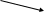
1. п

   равило треугольника:

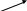
Определение 7. (произведения вектора на число)

Вектор называется произведением вектора на действительное число α (обозначается ), если

1. при α=0,

2. , сонаправлены при α>0,

3. , сонаправлены при α<0.

Свойства линейных операций над векторами

1. ;

2. ( =

3. α( ;

4. (α+β) = α +β ;

5. (α β) = α( ;

6. + = ;

7. +( ) = ;

8. 1 = .

Справедливость свойств 1÷8 следует из определений линейных операций над векторами. Докажем, например, справедливость свойства 2:

1. Линейно зависимые и независимые системы векторов

Определение 1. Вектор вида называется линейной комбинацией векторов .

Здесь некоторые действительные числа, называемые коэффициентами линейной комбинации.

Определение 2. Система векторов называется линейно зависимой системой (ЛЗС), если ( :

. (*)

Если же равенство (*) может быть выполнено только при = 0, то система векторов называется линейно независимой системой (ЛНС).

Утверждение 1. Система векторов является линейно зависимой системой тогда и только тогда, когда хотя бы один из векторов может быть записан в виде линейной комбинации других векторов.

Доказательство.

1. Пусть – линейно зависимая система. Тогда :

.

Пусть для определённости . Тогда = — — ,

то есть вектор может быть записан в виде линейной комбинации других векторов системы.

1. Пусть хотя бы один из векторов может быть записан в виде линейной комбинации других. Пусть для определённости это справедливо для вектора :

= — — .

Перепишем:

— — = .

Справедливо равенство (*), Следовательно, система векторов является линейно зависимой системой.

▲

Утверждение 2. Система векторов, содержащая нулевой вектор, является линейно зависимой системой.

Доказательство. Пусть для определённости = .

В этом случае справедливо равенство (*) при :

1 + + 0 .

Следовательно, система является линейно зависимой системой.

▲

Утверждение 3. Система векторов, содержащая линейно зависимую подсистему, является линейно зависимой.

Доказательство. Пусть для определённости векторы , входящие в систему , образуют линейно зависимую систему. Тогда справедливо равенство:

,

причём .

Следовательно, справедливо равенство:

,

в котором . Система является линейно зависимой.

▲

Утверждение 4. Векторы образуют линейно зависимую

систему тогда и только тогда, когда – коллинеарные векторы.

Доказательство.

1. Пусть векторы коллинеарны. Следовательно, : , отсюда, в силу утверждения 1, система является линейно зависимой системой.

2. Пусть векторы образуют линейно зависимую систему. Тогда, в силу утверждения 1, : . Следовательно, векторы являются коллинеарными.

▲

Утверждение 5. Векторы образуют линейно зависимую систему тогда и только тогда, когда они компланарны.

Доказательство.

1. Пусть векторы образуют линейно зависимую систему . В силу утверждения 1, хотя бы один из векторов может быть записан в виде линейной комбинации других. Пусть, для определённости, :

Следовательно, по определению получаем, что векторы являются компланарными.

1. Пусть - компланарны.

2a). Среди есть коллинеарная пара. В силу утверждения 4 эта пара образует линейно зависимую систему. В силу утверждения 3 векторы образуют линейно зависимую систему.

2б). Среди векторов нет коллинеарной пары. Приведём векторы к общему началу:

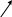
Достроим параллелограмм с диагональю . Получаем: . В силу утверждения 1 система является линейно зависимой системой.

▲

Утверждение 6. Любые 3 вектора на плоскости образуют линейно

зависимую систему.

Доказательство утверждения 6 проводится аналогично тому, как это

было выполнено для утверждения 5.

Утверждение 7. Любые четыре вектора в пространстве

образуют линейно зависимую систему.

Доказательство.

1. Пусть среди векторов нет некомпланарной тройки. Приведём векторы к общему началу, построим параллелепипед с диагональю и рёбрами, параллельными векторам

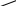
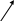
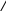
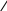
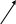
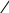
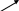
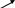
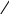
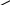
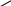
Получили: . В силу утверждения 1 система является линейно зависимой.

1. Пусть среди векторов содержится компланарная тройка. Тогда в силу утверждения 3 система является линейно зависимой.

▲

3.Базисы на прямой, на плоскости, в пространстве

Определение 1.

1. Вектор называется базисом на прямой, если

1) ,

2) , лежащий на этой прямой, можно записать в виде

(1)

1. Векторы образуют базис на плоскости, если

1) образуют линейно независимую систему,

2) , лежащий на плоскости, может быть записан в виде

(2)

1. Векторы образуют базис в пространстве, если

1. образуют линейно независимую систему,

2. может быть записан в виде

(3)

Теорема 1. Любой ненулевой вектор, лежащий на прямой, образует базис на прямой.

Теорема 2. Любая пара неколлинеарных векторов на плоскости образуют базис на этой плоскости.

Теорема 3. Любая тройка неколлинеарных векторов образует базис в пространстве.

Справедливость теорем 1,2,3 следует из утверждений 1-7, доказанных в предыдущем пункте.

Определение 2. Правые части равенств (1), (2), (3) называются разложениями векторов по базисам ; ; соответственно; числа α, β, γ называются координатами вектора в базисе.

Утверждение 1. Разложение по базису единственно.

Доказательство.

Пусть вектор имеет два разложения в базисе :

Но – базис является ЛНС .

Аналогично доказывается утверждение для базиса на прямой и в пространстве.

▲

Утверждение 2. При сложении векторов их координаты складываются. При умножении вектора на число все его координаты умножаются на это число.

Доказательство. Проведём доказательство для плоскости. Пусть – два вектора на плоскости, – базис на плоскости:

1)

2) | α

.

▲

Контрольный вопрос

Дана пирамида ABCD.

D

E

C

F

A

B

Пусть Найдите координаты вектора в базисе , если E, F – середины ребер BD, BC.

Ответ. . Координаты (0, , ).

4.Проекция вектора на ось. Свойства проекций. Система координат. Направляющие косинусы

Определение 1. Назовём осью прямую с заданным направлением:

Определение 2. Векторной проекцией вектора на ось , называется вектор , такой, что

1

) или 2)

Определение 3. Скалярной проекцией вектора на ось называется величина

,

где φ – угол между векторами , :

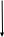
> 0

< 0

= 0

Свойства проекций

1. .

Справедливость этого утверждения следует из рисунка:

1. , α R

В справедливости можно убедиться, рассмотрев рисунки для случаев

1)α = 0, 2) α < 0, 3) α > 0.

Введём прямоугольную декартову систему координат в пространстве.

Для этого фиксируем точку О – “начало координат” и ортонормированный

базис

.

Направим ось OX вдоль вектора ; ось OY – вдоль вектора ; ось OZ

вдоль вектора . Пусть M – произвольная точка пространства. Разложим вектор

по базису

.

Числа x, y, z называются координатами точки M в системе координат

OXYZ .

Обозначение: M(x, y, z);

О

Z

чевидно : .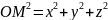

Y

M

X

Пусть α, β, γ – углы, которые вектор образует с осями OX, OY, OZ. Имеем:

.

Величины называются направляющими косинусами вектора . Очевидно:

.

Пусть A( ; B( . Имеем:

Отсюда ( см. рисунок )

A

O

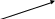
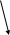
B

5.Скалярное произведение векторов и его свойства

Определение. Величина называется скалярным произведением векторов , .

Обозначение: , :

Очевидно, справедливы соотношения:

.

Свойства скалярного произведения

1. ( , ;

2. ( + ;

3. λ ( , (λ , , λ ;

4. ( , причём ( .

Доказательство свойств скалярного произведения

1. Справедливость следует из определения скалярного произведения.

2. ( + , ,

3. (λ , λ

4. Очевидно.

Выпишем полезные результаты: