lektsia_10_dlya_studentov_ON (1184631)
Текст из файла
17
Лекция 10
Уравнения плоскости и прямой в пространстве
1.Различные виды уравнения плоскости
Пусть ![]()
![]() некоторая точка;
некоторая точка; ![]()
![]() вектор нормали к искомой плоскости P. Напишем уравнение плоскости, проходящей через точку
вектор нормали к искомой плоскости P. Напишем уравнение плоскости, проходящей через точку ![]() перпендикулярно вектору
перпендикулярно вектору ![]() ( см. рисунок ).
( см. рисунок ).




P

Обозначим через ![]() текущую точку пространства.
текущую точку пространства.
Уравнение плоскости по точке и нормальному вектору
Дано:
(1)
Перепишем уравнение (1) в другом виде, получим общее уравнение плоскости (2):
Общее уравнение плоскости
(2)
Замечание.
Зная общее уравнение плоскости, можно выписать координаты вектора нормали. Они совпадают с коэффициентами при переменных x, y, z.
Примеры.
1. Выпишем уравнение плоскости, проходящей через точку (1,2,3) перпендикулярно вектору ![]() :
:
2. Выпишем уравнение нормали к плоскости ![]()
Пусть известны координаты трех точек (не лежащих на одной прямой), принадлежащих искомой плоскости ![]() Выпишем уравнение плоскости, проходящей через эти три точки .
Выпишем уравнение плоскости, проходящей через эти три точки .
Обозначим через ![]() текущую точку пространства. Очевидно, что эта точка принадлежит плоскости P тогда и только тогда, когда векторы
текущую точку пространства. Очевидно, что эта точка принадлежит плоскости P тогда и только тогда, когда векторы ![]() компланарны (см.рисунок):
компланарны (см.рисунок):





Запишем условие компланарности трех векторов:
Уравнение плоскости по трем точкам
(3)
Уравнение (3) называется уравнением плоскости по трем точкам.
Пусть некоторая плоскость дана своим общим уравнением:
Перепишем это уравнение в виде
иначе
Уравнение плоскости
«в отрезках»
(4)
Уравнение (4) называется уравнением плоскости «в отрезках». Отметим, что 
Величины ![]() имеют простой геометрический смысл. Их модули равны длинам отрезков, отсекаемых плоскостью от осей координат ( см. рисунок ):
имеют простой геометрический смысл. Их модули равны длинам отрезков, отсекаемых плоскостью от осей координат ( см. рисунок ):
Z



|c|
|b|
Y




|a|
X
Примеры.
1.Выпишем общее уравнение плоскости, проходящей через три точки ![]()
2.Вычислим отрезки, отсекаемые плоскостью ![]() от осей координат.
от осей координат.
Перейдем к составлению нормального уравнения плоскости. Пусть перед нами поставлена следующая задача:
написать уравнение плоскости, удаленной от начала координат на расстояние ![]() и имеющей нормальный вектор
и имеющей нормальный вектор![]() :
:
Обозначим через ![]() текущую точку пространства. Пусть
текущую точку пространства. Пусть ![]() проекция точки О ( начала координат ) на плоскость P ( см.рисунок );
проекция точки О ( начала координат ) на плоскость P ( см.рисунок );
Z
Q






M
A
O
Y


X

Очевидно, ![]() Имеем:
Имеем: ![]() Очевидно, что точка M принадлежит плоскости P тогда и только тогда когда
Очевидно, что точка M принадлежит плоскости P тогда и только тогда когда ![]()

Отсюда получаем:
(
Нормированное уравнение плоскости
5) Уравнение (5) называется нормированным уравнением плоскости. В нем ![]() направляющие косинусы вектора нормали, p
направляющие косинусы вектора нормали, p![]() расстояние от начала координат до плоскости P.
расстояние от начала координат до плоскости P.
Пусть известно нормированное уравнение плоскости (5).
Определение. Величина ![]() называется отклонением точки
называется отклонением точки ![]() от плоскости P.
от плоскости P.
Утверждение.
если точки О и М лежат по одну сторону от плоскости P
если точки О и М лежат по разные стороны от плоскости P
Доказательство. Рассмотрим случай, когда точки М и О лежат по разные стороны от плоскости Р (другой случай рассматривается аналогично).
Z
Q


Y
M



A

Y

O


X
Предположим, плоскость P задана своим общим уравнением. Чтобы нормировать уравнение плоскости, умножим обе части общего уравнения плоскости на так называемый нормирующий множитель μ, 
Искомое нормированное уравнение плоскости P
где
Примеры.
1.Запишем уравнение плоскости ![]() в нормальном виде:
в нормальном виде:
2. Найдём отклонение точки ![]() от данной плоскости, а также расстояние от точки
от данной плоскости, а также расстояние от точки ![]() до плоскости P.
до плоскости P.
Точки ![]() и О лежат по одну сторону от плоскости Р, так как
и О лежат по одну сторону от плоскости Р, так как ![]() .
.
2.Взаимное расположение двух плоскостей
Пусть две плоскости ![]() даны своими общими уравнениями:
даны своими общими уравнениями:
Исследуем взаимное расположение плоскостей ![]() .
.
1 случай. Плоскости параллельны, но не совпадают. В этом случае векторы ![]() должны быть коллинеарны, но плоскости должны быть различны.
должны быть коллинеарны, но плоскости должны быть различны.









2 случай. Плоскости совпадают. Векторы ![]() коллинеарны.
коллинеарны.
3 случай. Плоскости пересекаются ( по прямой ). В этом случае векторы ![]() должны быть неколлинеарны.
должны быть неколлинеарны.











Очевидно, что в случае 3 угол между плоскостями равен углу между нормалями: 
Рассмотрим следующую задачу.
Пусть две плоскости ![]() даны своими общими уравнениями:
даны своими общими уравнениями:
Необходимо выписать уравнения плоскостей, делящих пополам двугранные углы, образованные при пересечении плоскостей ![]() . Обозначим искомые плоскости как
. Обозначим искомые плоскости как ![]()














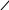







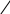






Обозначим через ![]() текущую точку пространства. Точка
текущую точку пространства. Точка ![]() принадлежит одной из плоскостей
принадлежит одной из плоскостей ![]() тогда и только тогда, когда эта точка равноудалена от плоскостей
тогда и только тогда, когда эта точка равноудалена от плоскостей ![]() :
:
Выбираем в последнем соотношении знаки «+» или «-» в обозначении «![]() », получим уравнения плоскостей
», получим уравнения плоскостей ![]()
Рассмотрим три плоскости ![]() , заданные своими общими уравнениями:
, заданные своими общими уравнениями:![]() .
.
Обсудим взаимное расположение плоскостей ![]()
Очевидно, возможны следующие случаи:
1) Плоскости параллельны (но не совпадают). В этом случае векторы нормалей должны быть коллинеарны:



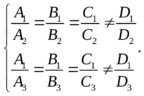
2) Плоскости пересекаются по трем параллельным прямым. В этом случае векторы нормалей должны быть компланарны, но система уравнений, состоящая из общих уравнений плоскостей, должна быть несовместна:



3
) Две плоскости параллельны между собой, но пересекаются с третьей плоскостью: 


Выпишите условия самостоятельно.
4) Три плоскости пересекаются вдоль прямой. В этом случае система, составленная из общих уравнений плоскостей, должна быть совместна, ранг матрицы системы должен быть равен 2. Отсюда получаем:


 .
. 5) Плоскости пересекаются в одной точке. В этом случае система, составленная из общих уравнений плоскостей, должна обладать единственным решением:



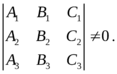
3.Различные уравнения прямой в пространстве
Пусть ![]()
![]() некоторая фиксированная точка пространства,
некоторая фиксированная точка пространства, ![]() фиксированный вектор. Составим уравнение прямой L, проходящей через точку
фиксированный вектор. Составим уравнение прямой L, проходящей через точку ![]() параллельно вектору
параллельно вектору ![]() (вектор
(вектор ![]() называется направляющим вектором прямой L ).
называется направляющим вектором прямой L ).
M
Обозначим через 
L




L
L

Канонические уравнения прямой
(1)
Уравнения (1) называются каноническими уравнениями прямой.
Замечание.
Канонические уравнения (1) понимаются как пропорции ![]() один или два из знаменателей могу быть равны нулю.
один или два из знаменателей могу быть равны нулю.
Пример.
Запишем уравнение прямой, проходящей через точку ![]() параллельно оси
параллельно оси ![]() .
.
Имеем: ![]() Отсюда канонические уравнения искомой прямой имеют вид
Отсюда канонические уравнения искомой прямой имеют вид
Перейдем к выводу параметрических уравнений прямой.
Пусть некоторая прямая задана своими каноническими уравнениями:
Приравниваем дробь величине ![]() (
(![]()
![]() некоторый параметр,
некоторый параметр, ![]()
Параметрические уравнения прямой, ![]()
(2)
Параметрические уравнения (2) удобно использовать при решении различных задач, например, для нахождения точки пересечения прямой и плоскости.
Пример.
Найдем координаты точки пересечения прямой ![]() с плоскостью
с плоскостью ![]() :
:
Запишем параметрические уравнения прямой ![]() :
:
P
L
A






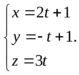
Подставим правые части этих уравнений в уравнение плоскости ![]() , получим:
, получим:
Отсюда точка пересечения прямой и плоскости имеет координаты ![]()
Перейдем к составлению уравнения прямой, проходящей через две точки ![]() и
и ![]() :
:
L



В качестве направляющего вектора берём вектор ![]() Обозначим через
Обозначим через ![]() текущую точку пространства. Точка M принадлежит искомой прямой тогда и только тогда, когда векторы
текущую точку пространства. Точка M принадлежит искомой прямой тогда и только тогда, когда векторы ![]() коллинеарны.
коллинеарны.
Тогда канонические уравнения прямой, проходящей через точки ![]() имеют вид:
имеют вид:
Уравнения прямой, проходящей через две фиксированные точки плоскости
(3)
Пример.
Запишем уравнения прямой, проходящей через точки ![]() и
и ![]()
Рассмотрим две непараллельные плоскости ![]() , определенные своими общими уравнениями ( см. рисунок):
, определенные своими общими уравнениями ( см. рисунок):
Непараллельные плоскости пересекаются вдоль прямой. Запишем уравнения плоскостей в систему:
Общие уравнения прямой
(4)











L




Уравнения (4) называются общими уравнениями прямой в пространстве.
Пусть известны общие уравнения прямой L (4). Как получить канонические уравнения этой прямой?
Сначала найдём координаты точки, лежащей на прямой L. Для этого подставим в систему (4), например, ![]() , найдём
, найдём ![]() . Может случиться, что система (4) при
. Может случиться, что система (4) при ![]() не имеет решений, тогда подставим
не имеет решений, тогда подставим ![]() или
или ![]() , найдем недостающие координаты. Можно доказать, что обязательно хотя бы один из вариантов
, найдем недостающие координаты. Можно доказать, что обязательно хотя бы один из вариантов ![]() ,
, ![]() ,
, ![]() позволит найти недостающие координаты точки, принадлежащей обеим плоскостям. Фиксируем точку
позволит найти недостающие координаты точки, принадлежащей обеим плоскостям. Фиксируем точку ![]() ,
, ![]() .
.
Характеристики
Тип файла документ
Документы такого типа открываются такими программами, как Microsoft Office Word на компьютерах Windows, Apple Pages на компьютерах Mac, Open Office - бесплатная альтернатива на различных платформах, в том числе Linux. Наиболее простым и современным решением будут Google документы, так как открываются онлайн без скачивания прямо в браузере на любой платформе. Существуют российские качественные аналоги, например от Яндекса.
Будьте внимательны на мобильных устройствах, так как там используются упрощённый функционал даже в официальном приложении от Microsoft, поэтому для просмотра скачивайте PDF-версию. А если нужно редактировать файл, то используйте оригинальный файл.
Файлы такого типа обычно разбиты на страницы, а текст может быть форматированным (жирный, курсив, выбор шрифта, таблицы и т.п.), а также в него можно добавлять изображения. Формат идеально подходит для рефератов, докладов и РПЗ курсовых проектов, которые необходимо распечатать. Кстати перед печатью также сохраняйте файл в PDF, так как принтер может начудить со шрифтами.












































