Lektsia_6_dlya_studentov_ON (Лекции по линейной алгебре АВТИ)

Лекция 6

Следствия теоремы о базисном миноре. Вычисление ранга матрицы

Напоминание.

Теорема о базисном миноре. Базисные столбцы (строки) образуют линейно независимую систему. Небазисные столбцы (строки) могут быть записаны в виде линейной комбинации базисных.

система столбцов (строк) матрицы А является линейно зависимой системой

det A=0

Одним из следствий теоремы является необходимое и достаточное условие равенства определителя нулю ( Следствие 1, доказано на предыдущей лекции ):

Докажем другие следствия теоремы о базисном миноре.

Следствие 2. Система из k столбцов высоты m, m < k, является линейно зависимой системой.

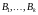Доказательство. Рассмотрим произвольную систему из k столбцов высоты m (m < k): . Составим матрицу из столбцов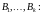

m строк

k столбцов

Очевидно: Rang A=r . Следовательно, среди столбцов матрицы есть хотя бы один небазисный. В силу теоремы о базисном миноре, небазисный столбец может быть записан в виде линейной комбинации базисных. Подсистема системы столбцов , состоящая из r базисных столбцов и указанного небазисного столбца, является линейно зависимой подсистемой системы столбцов . Было доказано ранее, что система столбцов, содержащая линейно зависимую подсистему, сама является линейно зависимую систему.

▲

Следствие 3. Если ранг матрицы меньше числа столбцов, то столбцы матрицы образуют линейно зависимую систему.

Определение 1. Подсистема системы столбцов называется максимальной линейно независимой подсистемой, если

1. Столбцы образуют линейно независимую систему;

2. Любая подсистема, состоящая большая, чем из s столбцов, является линейно зависимой подсистемой.

Утверждение. Различные максимальные линейно независимые подсистемы системы столбцов состоят из одного и того же числа столбцов.

Доказательство. Рассмотрим две максимально линейно независимые подсистемы системы столбцов . Пусть одна из подсистем содержит m столбцов, а другая – n столбцов. Предположим, m > n. Этого быть не может, так как вторая подсистема – максимальная, и любая подсистема из m векторов ( m > n ) должна являться линейно зависимой системой, то есть не может являться линейно независимой подсистемой. Аналогично докажем, что не может быть m < n, отсюда получаем, что может быть только m=n.

▲

Замечание. Все определения и утверждения, сформулированные выше, справедливы и для строк.

Определение 2. Рангом системы строк (столбцов) называется число строк (столбцов), входящих в максимальную линейно независимую подсистему системы строк (столбцов).

Следствие 4. Теорема о ранге матрицы. Ранг матрицы совпадает с рангом системы её строк (столбцов).

Доказательство. Пусть матрица А – матрица порядка m n, Rang A=r. Пусть максимальная линейно независимая подсистема системы столбцов состоит из k столбцов, то есть ранг системы столбцов матрицы равен k. Докажем, что k=r.

Предположим, k < r. Этого быть не может, так как подсистема, состоящая из r базисных столбцов, является линейно независимой системой (в силу теоремы о базисном миноре), и тогда максимальная линейно независимая подсистема не может состоять из k ( k < r ) столбцов.

Предположим, k > r. Запишем k столбцов, входящих в максимальную линейно независимую подсистему системы столбцов, в виде вспомогательной матрицы порядка m r. Очевидно, Rang . Число столбцов матрицы превосходит ранг этой матрицы, следовательно, в силу следствия 3 эта система должна являться линейно зависимой системой. Это противоречит тому, что столбцы матрицы составляют максимальную линейно независимую подсистему системы столбцов исходной матрицы А . Отсюда получаем, что неравенство k > r не может быть верным. Следовательно, может быть только k=r.

▲

Замечание. Теорема о ранге матрицы позволяет сформулировать новое определение ранга матрицы:

Определение 3. Рангом матрицы называется ранг системы строк (столбцов) матрицы.

Вычисление ранга матрицы

1. Метод окаймляющих миноров (о нем было сказано выше)

Пример. Найдем Rang A.

Находим ненулевой минор второго порядка и окаймляющие его миноры третьего порядка:

; ;

Отсюда получаем, что Rang A=2.

1. Метод элементарных преобразований.

Элементарными преобразованиями строк назовем:

1. перестановку строк;

2. сложение строк;

3. умножение строки на число.

Теорема (без доказательства). Элементарные преобразования строк (столбцов) матрицы, а также транспонирование матрицы и вычеркивание нулевой строки (столбца) не меняют ранга матрицы. ▲

Матрицы вида

(*)

называются ступенчатыми, или трапециевидными.

Идея метода элементарных преобразований состоит в следующем. Приведем элементарными преобразованиями матрицу к ступенчатому виду, в котором

(**) .

Очевидно, ранг матрицы вида (*) равен r, если выполнены условия (**). Тогда ранг и исходной матрицы равен r:

A = Rang A=r.

Пример. Найдем Rang A методом элементарных преобразований:

Решение:

Вычтем первую строку из второй

Вычтем вторую строку из третьей

вычеркиваем нулевую строку

Получаем ответ: Rang = Rang A=2.