Для студентов по предмету Математический анализУравнения математической физики (Кузнецов Л.А.)Уравнения математической физики (Кузнецов Л.А.)
4,9851346
2022-11-202022-11-20СтудИзба
ДЗ 11: Уравнения математической физики (Кузнецов Л.А.) вариант 13
Описание
Полный вариант все 15 задач:
Уравнения математической физики из задачника Л.А. Кузнецова 2005 года, задача №1, вариант 13
Решить смешанную задачу:
![]()
Уравнения математической физики из задачника Л.А. Кузнецова 2005 года, задача №2, вариант 13
Решить смешанную задачу:
![]()
Уравнения математической физики из задачника Л.А. Кузнецова 2005 года, задача №3, вариант 13
Решить смешанную задачу:
![]()
Уравнения математической физики из задачника Л.А. Кузнецова 2005 года, задача №4, вариант 13
Решить смешанную задачу:
![]()
Уравнения математической физики из задачника Л.А. Кузнецова 2005 года, задача №5, вариант 13
Решить смешанную задачу для данного неоднородного уравнения теплопроводности с нулевыми начальными и граничными условиями: U(x, 0) = 0, U(0, t) = 0, U(π, t) = 0
![]()
Уравнения математической физики из задачника Л.А. Кузнецова 2005 года, задача №6, вариант 13
Решить смешанную задачу:
![]()
Уравнения математической физики из задачника Л.А. Кузнецова 2005 года, задача №7, вариант 13
Решить смешанную задачу:
![]()
Уравнения математической физики из задачника Л.А. Кузнецова 2005 года, задача №8, вариант 13
Найти решение уравнения Лапласа ΔU = 0 в круговом секторе 0 < r < 1, 0 < ϕ < α (r, ϕ – полярные координаты, α < 2π), на границе которого искомая функция удовлетворяет следующим условиям:
![]()
Уравнения математической физики из задачника Л.А. Кузнецова 2005 года, задача №9, вариант 13
Решить задачу Дирихле для уравнения Лапласа ΔU = 0 в круге 0 ≤ r < 1, 0 ≤ ϕ < 2π (r, ϕ – полярные координаты), на границе которого искомая функция U(r, ϕ) имеет следующие значения:
![]()
Уравнения математической физики из задачника Л.А. Кузнецова 2005 года, задача №10, вариант 13
Решить смешанную задачу:
![]()
Уравнения математической физики из задачника Л.А. Кузнецова 2005 года, задача №11, вариант 13
Решить смешанную задачу:
![]()
Уравнения математической физики из задачника Л.А. Кузнецова 2005 года, задача №12, вариант 13
Решить смешанную задачу:
![]()
Уравнения математической физики из задачника Л.А. Кузнецова 2005 года, задача №13, вариант 13
Решить смешанную задачу:
![]()
Уравнения математической физики из задачника Л.А. Кузнецова 2005 года, задача №14, вариант 13
Решить смешанную задачу:
![]()
Уравнения математической физики из задачника Л.А. Кузнецова 2005 года, задача №15, вариант 13
Решить смешанную задачу для данного неоднородного волнового уравнения с нулевыми начальными и граничными условиями:
U(x, 0) = Ut(x, 0), U(0, t) = U(π, t)
![]()
Уравнения математической физики из задачника Л.А. Кузнецова 2005 года, задача №1, вариант 13
Решить смешанную задачу:
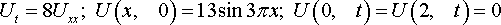
Уравнения математической физики из задачника Л.А. Кузнецова 2005 года, задача №2, вариант 13
Решить смешанную задачу:
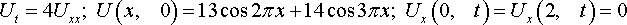
Уравнения математической физики из задачника Л.А. Кузнецова 2005 года, задача №3, вариант 13
Решить смешанную задачу:
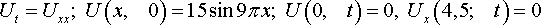
Уравнения математической физики из задачника Л.А. Кузнецова 2005 года, задача №4, вариант 13
Решить смешанную задачу:
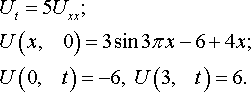
Уравнения математической физики из задачника Л.А. Кузнецова 2005 года, задача №5, вариант 13
Решить смешанную задачу для данного неоднородного уравнения теплопроводности с нулевыми начальными и граничными условиями: U(x, 0) = 0, U(0, t) = 0, U(π, t) = 0
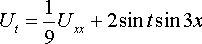
Уравнения математической физики из задачника Л.А. Кузнецова 2005 года, задача №6, вариант 13
Решить смешанную задачу:

Уравнения математической физики из задачника Л.А. Кузнецова 2005 года, задача №7, вариант 13
Решить смешанную задачу:
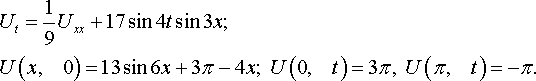
Уравнения математической физики из задачника Л.А. Кузнецова 2005 года, задача №8, вариант 13
Найти решение уравнения Лапласа ΔU = 0 в круговом секторе 0 < r < 1, 0 < ϕ < α (r, ϕ – полярные координаты, α < 2π), на границе которого искомая функция удовлетворяет следующим условиям:
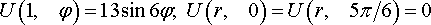
Уравнения математической физики из задачника Л.А. Кузнецова 2005 года, задача №9, вариант 13
Решить задачу Дирихле для уравнения Лапласа ΔU = 0 в круге 0 ≤ r < 1, 0 ≤ ϕ < 2π (r, ϕ – полярные координаты), на границе которого искомая функция U(r, ϕ) имеет следующие значения:
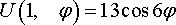
Уравнения математической физики из задачника Л.А. Кузнецова 2005 года, задача №10, вариант 13
Решить смешанную задачу:
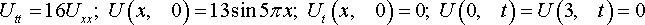
Уравнения математической физики из задачника Л.А. Кузнецова 2005 года, задача №11, вариант 13
Решить смешанную задачу:
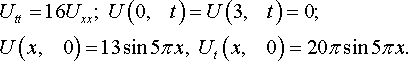
Уравнения математической физики из задачника Л.А. Кузнецова 2005 года, задача №12, вариант 13
Решить смешанную задачу:
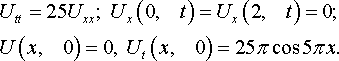
Уравнения математической физики из задачника Л.А. Кузнецова 2005 года, задача №13, вариант 13
Решить смешанную задачу:
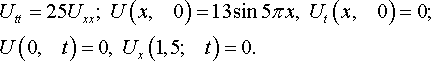
Уравнения математической физики из задачника Л.А. Кузнецова 2005 года, задача №14, вариант 13
Решить смешанную задачу:
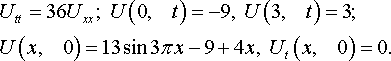
Уравнения математической физики из задачника Л.А. Кузнецова 2005 года, задача №15, вариант 13
Решить смешанную задачу для данного неоднородного волнового уравнения с нулевыми начальными и граничными условиями:
U(x, 0) = Ut(x, 0), U(0, t) = U(π, t)
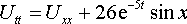
Характеристики домашнего задания
Предмет
Номер задания
Вариант
Программы
Теги
Просмотров
14
Качество
Идеальное компьютерное
Размер
526,6 Kb
Список файлов
XI-01-13.pdf
XI-02-13.pdf
XI-03-13.pdf
XI-04-13.pdf
XI-05-13.pdf
XI-06-13.pdf
XI-07-13.pdf
XI-08-13.pdf
XI-09-13.pdf
XI-10-13.pdf
XI-11-13.pdf
XI-12-13.pdf
XI-13-13.pdf
XI-14-13.pdf
XI-15-13.pdf
Комментарии
Нет комментариев
Стань первым, кто что-нибудь напишет!
 dmitry0376
dmitry0376
























