Для студентов МГТУ им. Н.Э.Баумана по предмету Кратные интегралы и рядыДомашнее заданиеДомашнее задание
5,00510
2024-11-202024-11-20СтудИзба
домашнее задание кратные интегралы и ряды мгту имени баумана 12 вариант
ДЗ 2: Домашнее задание вариант 12
Описание
ДОМАШНЕЕ ЗАДАНИЕ №2 ДЛЯ МТ, РК, Э5 и ФН
- рукописный текст
- все решения расписаны
- с чертежами
5 задач:
1) найти массу кривой С
![]()
2) в вариантах 1 – 15: вычислить криволинейный интеграл, убедившись в том, что подынтегральная функция является полным дифференциалом. Координаты точек А и В, а также функции даны.
![]()
3) Дана часть поверхности σ, вырезаемая поверхностью (поверхностями) S. Плотность поверхности σ равна µ . В вариантах 1 – 10 найти массу поверхности σ. В вариантах 11 – 20 найти координаты центра масс поверхности σ. В вариантах 21 – 30 найти момент инерции поверхности σ относительно осей координат и относительно начала координат.
![]()
4) Найти поток векторного поля F через часть плоскости σ, ограниченную координатными плоскостями. Сторона плоскости определяется нормалью, образующей острый угол с указанной осью.
![]()
5) Вычислить криволинейный интеграл по замкнутому контуру L двумя способами (непосредственно и по формуле Грина)
![]() Показать/скрыть дополнительное описание
Показать/скрыть дополнительное описание
- рукописный текст
- все решения расписаны
- с чертежами
5 задач:
1) найти массу кривой С

2) в вариантах 1 – 15: вычислить криволинейный интеграл, убедившись в том, что подынтегральная функция является полным дифференциалом. Координаты точек А и В, а также функции даны.

3) Дана часть поверхности σ, вырезаемая поверхностью (поверхностями) S. Плотность поверхности σ равна µ . В вариантах 1 – 10 найти массу поверхности σ. В вариантах 11 – 20 найти координаты центра масс поверхности σ. В вариантах 21 – 30 найти момент инерции поверхности σ относительно осей координат и относительно начала координат.
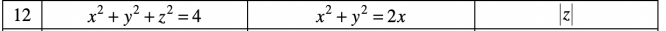
4) Найти поток векторного поля F через часть плоскости σ, ограниченную координатными плоскостями. Сторона плоскости определяется нормалью, образующей острый угол с указанной осью.

5) Вычислить криволинейный интеграл по замкнутому контуру L двумя способами (непосредственно и по формуле Грина)
 Показать/скрыть дополнительное описание
Показать/скрыть дополнительное описание.
Файлы условия, демо
Характеристики домашнего задания
Предмет
Учебное заведение
Семестр
Номер задания
Вариант
Программы
Просмотров
12
Качество
Скан рукописных листов
Размер
20,73 Mb
Список файлов
дз2.pdf
TR_2_Krivol_poverkhn_integraly.pdf
TR_2_zadacha_5.pdf
 МГТУ им. Н.Э.Баумана
МГТУ им. Н.Э.Баумана













