Для студентов МГТУ им. Н.Э.Баумана по предмету Дискретная математикаДомашнее задание 1 по дискретной математике. Задача ”Языки и конечные автоматы”.Домашнее задание 1 по дискретной математике. Задача ”Языки и конечные автоматы”.
5,0051
2022-09-142022-09-14СтудИзба
Задача: Домашнее задание 1 по дискретной математике. Задача ”Языки и конечные автоматы”. вариант 18
Описание
Автомат задан набором ({a, b}, {q1, q2, q3, q4, q5}, Qs, Qf ), где {a, b} — алфавит, Qs — множество начальных состояний (входов), Qf — множество конечных состояний (выходов), и
списком дуг с метками, определяющих допустимые переходы. Запись (i, j, a, b) означает, что
дуга (i, j), идущая из состояния qi в состояние gj, имеет две метки — a и b.
1. Построить граф автомата и найти язык L, допускаемый автоматом.
2. Детерминизировать автомат.
3. Построить графы автоматов, представляющих языки L0, L ∪ L0, L ◦ L0 и L∗.
4. Из построенных графов удалить λ-переходы.
Вариант 18. Входы Qs = {1}, выход Qf = {3, 4},
дуги: (1, 5, b), (1, 4, a), (2, 1, b), (3, 2, a), (4, 3, b), (5, 2, a), (5, 4, b).
L0 = {a^m b a^nb | n, m ≥ 0}.
![]()
списком дуг с метками, определяющих допустимые переходы. Запись (i, j, a, b) означает, что
дуга (i, j), идущая из состояния qi в состояние gj, имеет две метки — a и b.
1. Построить граф автомата и найти язык L, допускаемый автоматом.
2. Детерминизировать автомат.
3. Построить графы автоматов, представляющих языки L0, L ∪ L0, L ◦ L0 и L∗.
4. Из построенных графов удалить λ-переходы.
Вариант 18. Входы Qs = {1}, выход Qf = {3, 4},
дуги: (1, 5, b), (1, 4, a), (2, 1, b), (3, 2, a), (4, 3, b), (5, 2, a), (5, 4, b).
L0 = {a^m b a^nb | n, m ≥ 0}.
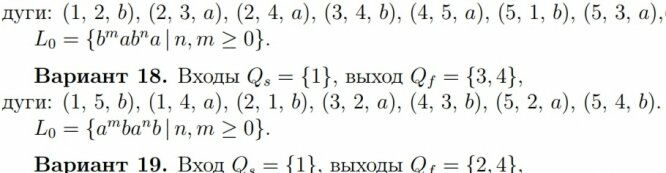
Файлы условия, демо
Характеристики решённой задачи
Предмет
Учебное заведение
МГТУ им. Н.Э.БауманаСеместр
Вариант
Просмотров
62
Качество
Скан печатных листов
Размер
685,94 Kb
Список файлов
ДМ_дз1.pdf
Yanya
14 сентября 2022 в 23:05
![](https://s.studizba.com/z.php?f=/templates/si/i/noavatar.png&w=100&h=100&t=1"){kind=avatar}
