Лекции в печатном виде (990087), страница 9
Текст из файла (страница 9)
И
Z1 Z2
И ИЛИ
Z3 Z4 Z5 Z6
Существует два типа вершин: вершина И, вершина ИЛИ.
Корень дерева – главная цель.
Вершина типа И: чтобьы решить задачу, надо решить все её подзадачи.
Вершина типа ИЛИ: чтобьы решить задачу, надо решить одну из её подзадач.
Вершина разрешима, если существует путь, связывающий целевую вершину с подзадачами.
Решающий подграф – это подграф исходного графа, показывающий, что начальная вершина разрешима.
Если в дереве есть вершины типа ИЛИ, то решающий подграф может быть не единственным.
Просмотр вершин от листьев к корню даёт план решения задачи.
В пример это могут быть: Z3 Z4 Z5
Z1 Z2
Или Z3 Z4 Z6
Одним из универсальных методов редукции является метод уменьшения различий. (Generel Problem Solver. Nowell, Show, Simon).
В этом методе редукция ведётся по принципу отщепления от главной задачи элементарных подзадач.
Sн => Sк
Три шага:
-
З
![]()
![]()
адача: преобразовать sн![]()
Sн в sк![]()
Sк, уменьшить различие.
адача: преобразовать sнЕсли D(sн,Sн)=0, то задача решениа.
-
Найти преобразование pi
![]()
P, устраняющее D(sн,Sн).
Е
Sк = s'
Spi
Spi, то останов. -
П
![]()
рименить pi.
рименить pi.
Sн => Sк
pi
Sн => Spi
s’ Spi => Sк
Выводы:
-
Может существовать неединственный оператор, устраняющий различия.
-
Ветвь может оказаться тупиковой.
Если различия можно упорядочить по важности, то строится следующая матрица.
| Dj \ Pj | P1 | P2 | … | Pn |
| V | ||||
| K |
В первую очередь применяются операторы, устраняющие главное различие.
Эффективность данного метода низкая.
Пример:
Обезьяна и банан.
s = (w, x, y ,z)
О – обезьяна, Б – банан, Я – ящик. Система координат одномерная.
w – координата О.
y
– координата ящика.
x = 1, если О на Я
0, иначе.
z = 1, если О схватила Б
0, иначе.
sн = (a, 0, b, 0)
sк = (c, 1, c, 1)
Операторы (преобразования):
P1(v) подойти в точку v.
P1(v) = ((x, 0, y, z)
(v, 0, y, z)
P2(t) передвинуть ящик в точку t.
P2(t) = ((x, 0, x, z) (t, 0, t, z))
P3 взобраться на ящик.
P3 = ((x, 0, x, z) (x, 1, x, z))
P4 схватить банан.
P4 = ((c, 1, c, 0) (c, 1, c, 1))
(a, 0, b, 0) (c, 1, c, 1)
Г лавное различие
z
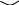
(a, 0, b, 0) Sp4
s’ Sp4 (c, 1, c, 1)
1p4
Р
азличия: D(a, 0, b, 0) Sp4
-
Я не в точке с
![]()
P2(c) -
О не в точке с
![]()
P1(c) -
О не на Я
![]()
P3
P2(c) P1(c) P3
(a, 0, b, 0) Sp4
P2(s’’ Sp4) Sp4
Различия: D(c, 0, c, 0) Sp4
О не на Я P3
P1(b)
Элементарная подзадача
P3
Обход снизу даёт решение: P1(b), P2(c), P3, P4.
Проблема взаимодействия подцелей.
Пример:
Мир роботов и кубиков.
X = {A, B, C, …} – множество кубоиков.
H = {1, 2, …} - множество рук.
CL(x) - кубик х свободен (на него можно ставить).
ON(x,y) - кубик х стоит на у.
ONT(x) - кубик х на столе.
HE(k)ё - к-тая рука робота свободна.
HL(x, k) - в к-той руке робота находится кубик.
Продукция имеет вид:
Левая часть = условие применимости продукции,
Правая часть = список дополнения (истинные предикаты) и список исключения (ложные предикаты).
P1(x, k) - взять кубик х со стола.
P1(x, k) = (ONT(x)&CL(x)&HE(k))
HL(x,k)& 
ONT(x)& CL(x)& HE(k)
P2(x, k) - поставить кубик х на стол рукой к.
P2(x, k) = (HL(x, k))
ONT(x)&CL(x)&HE(x)& HE(x, k)
P3(x, y, k) - поставить кубик х на кубик у к-той рукой.
P3(x, y, k) = (HL(x, y, k)&CL(y))
ONT(x, y)&CL(x)&HE(k)& HL(x, k)& CL(y)
P4(x, y, k) - снять кубик х с кубика у к-той рукой.
P4(x, y, k) = (HE(k)&ON(x, y)&CL(x))
CL(y)&HE(x, k)& HE(k)& CL(x)& ON(x, y)
Последовательная реализация целей. (однорукий робот).
A
С
C
А
B
B
Sн Sк
Sк = (ONT(B), ON(C, B), ON(A, C), CL(A), HE)
ONT(B) ON(C,B) ON(A, C) CL(A) HE
+ + +
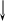
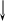P3(A, C)
P3(C, B)
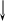
P1(C)
CL(B)
HL(C)
CL(C)
HL(A)
P1(A)
P4(A, X)
+
P4(C, X)
CL(C)
HE
ONT(C)
ON(C,X)
CL(C)
HL(C)
CL(C)
HE
ONT(C)
ON(C,X)
CL(C)
HL(C)
+
+ + - + (X=A) + + + + - + (X=A) +
-
ON(C, B): P4(C, A), P3(C, B)
ON(A, C): P1(A), P3(A, C)
Решение: P4(C, A), P3(C, B), P1(A), P3(A, C)
Параллельная реализация подцелей.
(двурукий робот)
-
Независимые подцели. n одноруких роботов.
-
Зависимые подцели.
А
С
B
B
C
A
Sн Sк
ON(C, B), ON(A, C)
ON(C, B)
ON(A, C)
P4(C, A, 1, P3(C, B, 1)
P3(A, C)
HL(A, 2)
CL(C)
+
P1(A, 2)
P1(A,X,2)
HE(2)
ONT(A)
CL(A)
+ +
P2(C, 2)
P1(C,A,2)
P4(X,A,2)
HL(2)
ON(X,A)
CL(X)
+ + (X=C) + (X=C)
P4(C, A, 2) t1 P2(C, 2) t3 P1(A, 2) t4 P3(A, C, 2)
Р
ука 2 t
P4(C, A, 1) t1 P3(C, B, 1) t2
Р ука 1 t
Согласование подцелей.
-
Супервизор. (Следит за процессом и строит реальный план.)
P1(A, 2) t3 P3(A, C, 2) t4
Р ука 2 t
P4(C, A, 1) t1 P3(C, B, 1) t2
Р ука 1 t
Итоговое решение:
P4(C, A, 1), P3(C, B, 1) || P1(A, 2), P3(A, C, 2)
Последовательное выполнение: t = t4 + t3 + t1 + t2
Параллельное выполнение: t = t4 + max(t3, t1) + t2
-
Частично упорядоченные подцели.
P4(C, A, 1)
P3(C, B, 1)
P1(A, 2)
P3(A, C, 2)
ON(C, B), ON(A, C)
P3(A, C, 2)
ON(C, B)&CL(C)&HL(2)
ON(1, B)&CL(1)
HL(A, 2)
P1(A, 2)
P3(C, B, 1)
HE(2)&CL(C)&ONT(A)
HL(1, 1)&CL(B)
HL(C, 1)&CL(B)&HE(2)&CL(A)&ONT(A)
P4(C, A, 1)
HE(1)&CL(C)&ON(C, X)
Таблица решений:
| ТР | P1 | P2 | … | Pn |
| ONT(X) | 1 | (0) | ||
| HE | 1 | (0) | ||
| ON(X, Y) | (0) | (0) | ||
| CL(X) | 1 | (0) | ||
| HL(X) | 1 | |||
| ONT(X) | 0 | 1 | ||
| HE | 0 | 1 | ||
| ON(X, Y) | ||||
| CL(X) | 1 | |||
| HL(X) | 1 | (0) |
![](https://s.studizba.com/z.php?f=/templates/si/i/noavatar.png&w=100&h=100&t=1"){kind=avatar}
