N_N_EOM (722406), страница 3

Просмтор этого файла доступен только зарегистрированным пользователям. Но у нас супер быстрая регистрация: достаточно только электронной почты!

Текст из файла (страница 3)

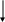
мал. 6-8 а) (Каган стр. 214)

Початкове ділене X заноситься в PгX, а дільник Y – в старші розряди Pг1Y. Дільник зсувається вправо шляхом косої передачі з Pг1Y в Pг2Y і прямої передачі з Pг2Y в Pг1Y. Віднімання дільника виконується підсумувуванням додаткового коду дільника. Цифри частки залишків, які визначають по знаку часткових залишків, фіксується в регістрі Pг1Z шляхом послідовного занесення їх в молодший розряд Pг1Z і зсуву вмісту Pг1Z з допомогою косої передачі в Pг2Z і прямої з Pг2Z в Pг1Z.

Недоліком такого АЛП є подвійна довжина суматора і його регістрів.

2. Ділення з нерухомим дільником і зсувом вліво діленого.

Цей спосіб дозволяє будувати АЛП з суматором одиночної довжини (малюнок 6-8, б).

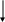
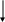
малюнок 6-8, б (Каган стр. 214)

Тут нерухомий дільник Y зберігається в PгY, а ділене X, зсуваючись вліво відносно Y, знаходиться в двох регістрах: старші розряди X – в Pг1X,
а молодші – в Pг2X. Ділення починається з зсуву вліво діленого X шляхом косої передачі його в PгCm і Pг3X і відповідних прямих передач в Pг1X. Далі на вхід суматора подається зсунуте вліво ділене, утворюється частковий залишок шляхом підсумовуванням додаткового коду дільника, і наступна цифра частки заноситься в звільнений при зсуві X розряд Pг2X.

Арифметично-логічний пристрій розглянутого типу широко застосовується для ділення.

Алгоритм ділення з нерухомим дільником з відновленням залишку.

1. Берутся модулі від діленого і дільника.

2. Початкове значення часткового залишку покладається рівним старшим розрядам діленого.

3. Частковий залишок подвоюється шляхом зсуву на один розряд вліво.
При цьому в звільнений при зсуві молодший розряд часткового залишку заноситься наступна цифра діленого.

4. З зсунутого часткового залишку віднімається дільник і аналізується знак результату віднімання.

5. Наступна цифра модуля частки рівна 1, якщо результат віднімання додатній, і 0, якщо від’ємний. В останньому випадку значення остачі відновлюється до того, яке було до віднімання.

6. Пункти 3, 4 і 5 послідовно виконуються для одержання всіх цифр модуля частки.

7. Знак частки плюс, якщо знаки діленого і дільника однакові, в іншому випадку – мінус.

Розглянемо тепер більш детально ділення в АЛП з нерухомим дільником. Структурна схема АЛП дана на малюнку 6-9.

малюнок 6-9 (Каган стр. 215)

Схема містить: суматор Cm; вхідний регістр Pг1 для збереження дільника; вхідний регістр суматора PгA, в який поступає прямий або зворотній код дільника; вихідний регістр суматора PгCm, в якому утворюється частковий залишок; регістри діленого PгB (старші розряди) і Pг2 (молодші розряди); допоміжний регістр Pг2’ для зсуву діленого, тригери знаків діленого і дільника ТгЗн1 і ТгЗн2; лічильник циклів СчЦ для підрахунку числа одержаних цифр частки. Одержані в процесі ділення цифри частки заносяться в звільнені розряди Pг2’.

Мікропрограма ділення для випадку додатніх чисел приведена на
малюнку 6-10. Пояснемо процедуру відновлення остачі.

малюнок 6-10 (Каган стр. 217)

Якщо віднімання дає від’ємний результат (См[0] = 1), то попередній частковий залишок, який зберігається в PгB, передається в PгCm, для чого попередньо обнулюється PгA. В PгCm прийом здійснюється з зсувом вліво на
1 розряд. Це забезпечує відновлення попереднього часткового залишку і зміщення його відносно дільника перед наступним відніманням.

Мікропрограма, яку ми розглядаємо, призначена для обробки додатніх чисел. А також її можна легко перетворити для обробки чисел з любими знаками,
які представленні в прямому коді. Для цього треба внести такі зміни:
після прийому операндів в PгB, Pг2 і Pг1 значення знакових розрядів X і Y передаються в тригер знака – відповідно ТгЗн1 і ТгЗн2. Потім в PгB [0] і Pг1 [0] заноситься 0, тобто виконується перехід до модулів X і Y. Розряд знаку частки встановлюється в 0 при ТгЗн1 = ТгЗн2 і в 1 в протилежному випадку.

Розглянутий метод ділення носить назву ділення з відновленням залишку. Недоліком цього методу є необхідність введення спеціального такту для відновлення залишку.

Звичайно в ЕОМ для ділення використовується другий метод – ділення без відновлення залишку.

Алгоритм ділення з нерухомим дільником без відновлення залишку.
Пункти 1-3 співпадають з алгоритмом ділення з відновленням залишку.

4. З зсунутого часткового залишку віднімається дільник, якщо залишок додатній, і до зсунутого часткового залишку додається дільник, якщо залишок від’ємний.

5. Наступна цифра модуля частки рівна 1, якщо результат віднімання додатній, і 0, якщо від’ємний.

Пункти 6, 7 співпадають з попереднім алгоритмом.

Можна показати, що часткові залишки після виконання додавання при діленні без відновлення залишку одержуються такі самі, як і залишки після зсуву відновленного залишку при діленні з відновленням залишку.

Дійсно, оскільки зсув часткового залишку на один розряд вліво є еквівалентом множення його на два, одержимо: 2*a – b = 2*(a – b) + b, (6-5),
де a – частковий залишок; b – дільник.

Аналогічно

2ⁿa = {…{[(a – b)*2 + b] + b}*2 + … + b}. (6-6)

Ділення без відновлення залишку завжди потребує для одержання одної цифри частки тільки додавання або віднімання з зсуву часткового залишку.

Мікропрограма ділення цілих додатніх чисел без відновлення залишку у своїй початковій частині співпадає з мікропрограмою ділення без відновлення залишку. Різниця з’являєтья після формування знаку частки. На малюнку 6-11 приведена частина мікропраграми ділення без відновлення залишку після мікрокоманди фіксації знаку частки.

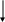
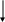
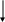
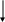
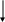
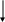
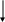
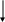
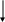
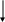
малюнок 6-11 (Каган стр. 219)

Блок-схема показує, що поки невизначені всі цифри частки (СчЦ <> 0),
в залежності від знаку часткового залишку або підсумовується Y (при См [0] = 1), або віднімається Y (при См [0] = 0). В одержаному новому частковому залишку аналізується знак і в ньому визначається цифра частки. Після завершення всіх циклів ділення (СчЦ = 0) видається реультат. При цьому якщо залишок від’ємний, то він відновлюється шляхом підсумуванням Y.

Ділення чисел, що представленні в залежності від знаку прямим доповнюючим кодом, можна зробити не переходячи до модулів. При цьому алгоритм ділення є подібним до розглянутих.

Відмінності заключаються в наступному (для випадку ділення без відновлення залишку):

1. Так як ділене і дільник можуть мати різні знаки, то дія з частковим залишком (додавання або віднімання Y) залежать від знаку залишку і дільника і визначаються таблицею 6-4.

Знак залишку	Знак дільника	Дія
+	+	Віднімання Y
+	-	Додавання Y
-	+	Додавання Y
-	-	Віднімання Y

таблиця 6-4 (Каган стр. 219)

Якщо знак залишку співпадає з знаком дільника, то z_i = 1, інакше z_i = 0.

2. Якщо X > 0 і Y < 0, то частку необхідно збільшити на одиницю.

Якщо X 0, то частку необхідно збільшити на одиницю у випадку залишку від ділення, яке не дорівнює нулю.

Якщо X < 0 і Y < 0, то частку необхідно збільшити на одиницю у випадку залишку від ділення, яка рівна нулю.

Ділення правильних дробів виконується так, як і ділення цілих.
Різниця заключається тільки у тому, що ділене має, як правило, таку ж довжину, як дільник. Але можна допустити, що ділене має ще n молодших розрядів, які рівні нулю. Тоді стає ясно, що алгоритм ділення дробів нічим не відрізняється від алгоритму ділення цілих.

2.8.1 Арифметичний пристрій з фіксованою крапкою (Чу стр. 130-135)

Арифетичний пристрій виконує арифметичні команди, що зберігаютьсяв пам’яті обчислювальної машини. У тому випадку, якщо цей пристрій додає і віднімає додаткові коди паралельно, тобто ми виконуємо арифметичні дії над всіма розрядами одночасно, то це є паралельний арифметичний пристрій.
В такому пристрої є схема паралельного суматора або паралельного віднімання.

Двійкові числа, що представляються знаковим бітом і двійковим модулем числа, в якому, між цілою і дробною частиною розміщені завжди на одному місці, називаються двійковими числами з фіксованою крапкою. Є два способи представлення таких чисел: модуль – ціле число, або модуль – простий дріб. Якщо кома розміщена між знаковим бітом і старшим бітом числа, то будь-яке число в такому форматі є дробовим. Якщо ж кома розміщена справа від молодшого біта значущої частини, то число є цілим.

Знаковий біт

1 Число 22

S

малюнок 4.1 (Чу стр. 131)

Характеристики

Список файлов реферата