15153 (686455), страница 3
Текст из файла (страница 3)
Если произведение цепных темпов заменить соответствующим базисным темпом роста за весь изучаемый период, то получим формулу среднего темпа, имеющую следующий вид:
 (2.7)
(2.7)
где Т — средний темп роста;
Уn— абсолютный уровень конечного периода;
У0 — абсолютный уровень начального периода;
n — число периодов, равное числу лет минус единица (m-1).
Если абсолютная скорость прироста уровня динамического ряда характеризуется величиной абсолютного прироста, то относительная — темпом прироста.
Темп прироста — это отношение абсолютного прироста к уровню, принятому за базу. Темпы прироста, как и темпы роcта, могут быть выражены в форме коэффициентов и процентов. Коэффициент прироста показывает, на какую долю увеличился или уменьшился уровень по сравнению с базисным:
 (2.8)
(2.8)
где ΔК — коэффициент прироста уровня, выраженный в долях;
ΔУn— значение абсолютного прироста уровня;
У0 - уровень, принятый за базу.
Темп прироста, выраженный в процентах, показывает, на сколько процентов увеличился или уменьшился отчетный уровень по сравнению с базисным:
ΔТ=ΔК*100 (2.9)
Темпы прироста, как и темпы роста, могут быть рассчитаны базисным и цепным способами. Между темпами прироста и темпами роста существует непосредственная связь, т.е. если темп прироста выражен в процентах, то он на 100 % меньше темпа роста:
ΔТ==Т-100 (2.10)
Темпы прироста могут быть выражены положительными (+) и отрицательными (-) значениями. Положительное значение темпа указывает на рост отчетного уровня по сравнению с базисным, отрицательное — на его снижение В последнем случае говорят о темпе снижения.
Темпы прироста за весь промежуток времени в динамическом ряду могут быть охарактеризованы при помощи их среднего значения.
При расчете среднего темпа прироста можно исходить из значения среднего темпа роста:
ΔТ==Т-100, (2.11)
где ΔТ — средний темп прироста;
Т — средний темп роста.
При анализе динамического ряда необходимо выяснить, какими абсолютными значениями выражаются темпы роста, темпы прироста уровня, так как в некоторых случаях при снижении (замедлении) темпов роста абсолютный прирост может возрастать. Поэтому при анализе динамического ряда в статистике вычисляется абсолютное значение одного процента прироста (снижения).
Абсолютное значение одного процента прироста представляет собой отношение абсолютного прироста к темпу прироста, выраженному в процентах:
 (2.12)
(2.12)
После несложного преобразования формулы получим:
 (2.13)
(2.13)
Это означает, что абсолютное значение одного процента прироста (снижения) равно 0,01 базисного уровня.
Проведем расчет вышеперечисленных показателей в таблице 2.1.
Таблица 2.1. Показатели динамики уровня оплаты корма (кг/т к.ед.) в сельскохозяйственной организации за 2005 – 2009 г.г.
| Годы | Уровень оплаты корма, кг/т к.ед. | Абсолютные приросты, кг/т к.ед. | Темпы роста, % | Темпы прироста, % | Абсолютное значение 1% прироста | |||
| базисные | цепные | базисные | цепные | базисные | цепные | |||
| Y | | | | | | | | |
| 2005 | 98 | - | - | 100 | 100 | - | - | - |
| 2006 | 99 | 1 | 1 | 101,0 | 101,0 | 1,0 | 1,0 | 0,98 |
| 2007 | 112 | 14 | 13 | 114,3 | 113,1 | 14,3 | 13,1 | 0,99 |
| 2008 | 106 | 8 | -6 | 108,2 | 94,6 | 8,2 | -5,4 | 1,12 |
| 2009 | 133 | 35 | 27 | 135,7 | 125,5 | 35,7 | 25,5 | 1,06 |
| В среднем | 109,4 | 8,8 | 106,9 | 6,9 | 1,0 | |||
Данные таблицы 2.1 свидетельствуют о том, что уровень оплаты кормов в 2006 и 2007 гг. по сравнению с 2005 годом увеличились на 1 и 13 кг/т к.ед. соответственно, в 2008 году по сравнению с 2005 годом – уровень оплаты корма пошел на спад (-6 кг/т к.ед.).
Темп роста в среднем составил 106,9 %, а абсолютное значение в среднем составило 1 кг/т. к.ед.
Выявление общей тенденции развития признака может быть проведено с использованием приемов аналитического выравнивания динамического ряда. Аналитическое выравнивание ряда динамики обычно осуществляется следующими способами: по прямой линии; по гиперболе; по параболе второго порядка.
Способы аналитического выравнивания хотя и содержат в себе ряд условностей, но более совершенны по сравнению с укрупнением периодов и скользящей средней. Аналитическое выравнивание облегчает выявление общей тенденции и изучение сезонных колебаний в характере динамического ряда. Выбор того или иного способа аналитического выравнивания обусловлен характером (типом) динамики. Характер динамики может быть выражен в виде аналитических уровней, которым на координатном графике соответствует определенная линия — прямая, парабола, гипербола и т. п.
Тип динамики целесообразно учитывать при выборе способов аналитического выравнивания динамических рядов. Если динамический ряд имеет более или менее стабильные абсолютные приросты, то выравниваемый динамический ряд может быть выражен в виде прямой линии. При этом на координатном графике фактические уровни ряда наиболее целесообразно показать прямолинейно.
При выравнивании по прямой линии закономерно изменяющийся уровень признака рассчитывается как функция времени:
 (2.14)
(2.14)
где Уt - выровненные значения уровней ряда;
t - периоды или моменты времени, к которым относятся уровни;
а, b - параметры уравнения (искомой прямой).
Для расчета параметров уравнения прямой линии обычно применяют способ наименьших квадратов, в основе которого лежит следующее требование: сумма квадратов отклонений фактических уровней ряда (У) от выровненных
и лежащих на искомой линии уровней (У) должна иметь минимальное значение, т. е.

(2.15)
Этому требованию удовлетворяет система нормальных уравнений, которые в соответствии с обозначениями уравнения могут быть записаны в следующей форме:

(2.16)
Где у – значение уровней фактического ряда динамики;
t – порядковые номера периодов или моментов времени;
n – число уровней фактического ряда динамики.
Приведенную систему нормальных уравнений можно упростить, если срединный уровень ряда условно принять за начальный уровень. В этом случае Σt=0, а система уравнений примет следующий вид:
о
(2.18)
ткуда параметры уравнений а, b выразятся так:
(2.17)
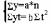
Определив параметры а, b, легко найти выровненные значения уровней у и изобразить их графически в виде прямой линии.
В нашем случае динамический ряд имеет более или менее стабильные абсолютные приросты, следовательно, выравниваемый динамический ряд может быть выражен в виде прямой линии.
Таблица 2.2. Фактический и выровненный уровень оплаты корма (кг/т к.ед.) в сельскохозяйственной организации за 2005 – 2009 г.г.
| Годы | Фактический уровень оплаты корма, кг/т к. ед. | Поряд-ковый номер уровней | Отклонение порядкового номера уровня от срединного номера | Квадрат откло-нений | Произве-дение значений | Выровненный уровень оплаты корма, кг/т к. ед |
| y | n | t | T2 | yt | | |
| 2005 | 98 | 1 | -2 | 4 | -196 | 94,2 |
| 2006 | 99 | 2 | -1 | 1 | -99 | 101,9 |
| 2007 | 112 | 3 | 0 | 0 | 0 | 109,6 |
| 2008 | 106 | 4 | 1 | 1 | 106 | 117,3 |
| 2009 | 133 | 5 | 2 | 4 | 266 | 125 |
| итого | 548 | - | 0 | 10 | 77 | 548 |
![]()
















