86219 (612685), страница 2

Просмтор этого файла доступен только зарегистрированным пользователям. Но у нас супер быстрая регистрация: достаточно только электронной почты!

Текст из файла (страница 2)

Если для введенных параметров выполняется условие

, (8)

то следует повторить ввод параметров для пятиугольника.

б) При построении отрезка СВ снова может возникнуть конфигурация, приводящая к невыпуклому пятиугольнику.

Составим уравнение прямой АВ

.

Неравенство (4) для точек и прямой АС после упрощений принимает вид

(9)

Если для введенных параметров выполняется условие (9), то следует повторить ввод параметров для пятиугольника.

с) При построении отрезка СВ снова может возникнуть конфигурация, приводящая к невыпуклому пятиугольнику.

B

Чтобы избежать данной конфигурации необходимо потребовать, чтобы ордината точки В была меньше ординаты точки Е, то есть чтобы выполнялось следующее неравенство:

(10)

Если для введенных параметров выполняется условие (10), то следует повторить ввод параметров для пятиугольника.

Координаты всех вершин пятиугольника определены, и пятиугольник можно построить на экране компьютера.

По условию: , следовательно, этими углами можно замостить окрестность точки.

Т аким образом, для составления программы изображения паркета из данного пятиугольника на экране компьютера, достаточно рассмотреть три пятиугольникa: ABCDE, A₂B₂C₂D₂E₂ и A₃B₃C₃D₃E₃ (рис. 6).

Рис.6

Е₂

А₂

С₂

В₂

D₂

Е₃

А₃

С₃

В₃

D₃

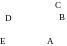
Рассмотрим математическую модель для составления программы изображения паркета на экране компьютера.

Координаты вершин пятиугольникa ABCDE :

Пятиугольник A₂B₂C₂D₂E₂ получаются из пятиугольникa ABCDE с помощью центральной симметрии относительно середины отрезка АВ.

Тогда координаты вершин пятиугольникa A₂B₂C₂D₂E₂:

Пятиугольник A₃B₃C₃D₃E₃ получаются из пятиугольникa ABCDE с помощью:

1. симметрии относительно оси Ох;

2) поворот на угол t относительно точки А; (получаем A’₃B’₃C’₃D’₃E’₃)

3 ) параллельный перенос на вектор D’₃ B

Координаты вершин пятиугольникa A₃B₃C₃D₃E₃:

Таким образом, для составления паркета из данного пятиугольника достаточно построить три пятиугольникa: ABCDE, A₂B₂C₂D₂E₂ и A₃B₃C₃D₃E₃.

Программа построения и примеры паркета из рассмотренного пятиугольника представлены в приложении 3 и в приложении 4 соответственно.

После наложения условий (7)-(10) получаем паркет из выпуклых пятиугольников. Если снять некоторые условия из условий (4), тогда могут возникнуть случаи, когда шестиугольник выраждается в пятиугольник или четырехугольник, а пятиугольник вараждается в четырехугольник.

Заключение

В книгах [1; 2] рассмотрены различные типы пятиугольников и шестиугольников, которыми можно замостить плоскость, но, к сожалению, в них нет математической теории для моделирования этих пятиугольников и шестиугольников. В настоящей работе была выполнена формализация поставленной задачи, впервые построены модели, разработаны программы для построения паркетов из некоторых типов пятиугольников и шестиугольников предложенных в книге [2], а так же был проведен эксперимент по тестированию разработанных программ. Для математического моделирования применялся метод координат и векторный метод. В работе впервые выведены условия выпуклости данных типов пятиугольника и шестиугольника. Все программы разработаны в среде Турбо Паскаль и позволяют наглядно моделировать различные паркеты.

Литература

1. Гарнер М. Путешествие во времени. – М.: Мир, 1990. – 341 с.

2. Математический цветник. /Сост. и ред. Д.А.Кларнер. М.: Мир, 1983. – 494 с.

3. Совертков П.И., Енбаева Е.А. Равносторонний пятиугольник Рейнхардта// Элементарная математика, математическое образование, геометрия и информатика №3, СПб.: Мифрил, 2000, с. 68-75.

4. Совертков П.И.,Слива М.В., Хохлов Д.Н. Геометрический паркет – I // Элементарная математика, математическое образование, геометрия и информатика № 4, СПб.: Мифрил, 2000, с. 3-19.

Приложение 1

Программа для построения паркета из шестиугольника.

Program shestiugolnik;

uses graph;

label 1,2;

var a,z4,s4,b,d,f,xx,yy,grv,grm,x0,x1,j,i,x5,y5,x2,x3,x4,y0,t, u,y1,y2,y3, y4, z1,z2,z3,s1,s2,s3:integer;tex:string; q,w,e:real;

begin

grv:=detect;

initgraph(grv,grm,'d:\bp\bgi');

1: writeln('gelaete vvesti parametri?(y/n)');

readln(tex);

if tex='n' then goto 2;

writeln('vvedite storoni');

readln(a,b,d,f);

xx:=-10;yy:=-10;t:=xx;u:=yy;

writeln('vvedite ugli');

readln(q,w,e);

q:=q*pi/180;w:=w*pi/180;e:=e*pi/180;

i:=trunc(sin(e)*(f*sin(q)-d*sin(e)));

j:=trunc(sin(e)*(b*sin(w)-d*sin(e)));

if (i<0)and(j<0) then begin

if (we)and(q>0)and(q0)and(w0)

and(e<180) then begin

for j:=1 to trunc(900/a) do begin

for i:=1 to trunc(600/(d*sin(e))) do begin

x0:=xx+0;y0:=yy+0;

x1:=xx+a;y1:=yy;

x2:=xx+trunc(A+B*COS(W));y2:=yy+trunc(B*SIN(W));

x4:=xx+trunc(D*COS(E));y4:=yy+trunc(D*SIN(E));

x3:=xx+trunc(A+D*COS(e));y3:=yy+trunc(d*sin(e));

x5:=trunc(f*cos(q))+xx;y5:=trunc(f*sin(q))+yy;

z1:=trunc(f*cos(q)-a)+xx;s1:=trunc(f*sin(q))+yy;

z2:=trunc(f*cos(q)-a-b*cos(w))+xx;s2:=trunc(f*sin(q)-b*sin(w))+yy;

z3:=trunc(f*cos(q)-a-d*cos(e))+xx;s3:=trunc(f*sin(q)-d*sin(e))+yy;

z4:=trunc(f*cos(q)-d*cos(e))+xx;s4:=trunc(f*sin(q)-d*sin(e))+yy;

xx:=xx+trunc(d*cos(e));yy:=yy+trunc(d*sin(e));

line(x0,y0,x1,y1);

line(x1,y1,x2,y2);

line(x2,y2,x3,y3);

line(x3,y3,x4,y4);

line(x4,y4,x5,y5);

line(x5,y5,x0,y0);

line(x5,y5,z1,s1);

line(z1,s1,z2,s2);

line(z2,s2,z3,s3);

line(z3,s3,z4,s4);

line(z4,s4,x0,y0);

end;

xx:=t+trunc(a+a-f*cos(q)+b*cos(w));t:=xx;

yy:=u+trunc(b*sin(w)-f*sin(q));u:=yy;

end;

end else begin writeln('vi vveli nevernie parametri');goto 1;end;

end else begin writeln('vi vveli nevernie parametri');goto 1;end;

readln;

2:

closegraph;

e nd.

Приложение 2

Пример 1.

Vvedite storoni

95 65 75 45

vvedite ugli

120 25 75

Пример 2.

Vvedite storoni

50 25 38 20

vvedite ugli

110 29 65

Приложение 3

Программа для построения паркета из пятиугольника.

program dip2;

uses graph;

label 1,2;

var a,a1,a2,a3,a4,a5,a6,a7,a8,a9,a10,a11,a12,i,j,xx,yy,b,c,vv,xa, xb,xc, xd, xe,ya,mm,yb,yc,yd,ye,x,y,grv,grm:integer;aa,qq,dd,tt,m1:real; tex:string[1];

begin

initgraph(grv,grm,'d:\bp\bgi');

1: writeln('gelaete vvesti parametri?(y/n)');

readln(tex);

if tex='n' then goto 2;

writeln('vvedite');readln(aa,dd,a,b,c);

aa:=aa*pi/180;dd:=dd*pi/180; tt:=aa+dd-pi; qq:=dd-pi;

vv:=trunc(a*sin(aa+dd)-b*sin(dd));

m1:=(a*sin(aa+dd)-b*sin(aa))*(a*sin(aa)-a*sin(dd)-b*sin(-dd+aa));

mm:= trunc(m1);

a1:=trunc(b*cos(aa)); a2:=trunc(b*sin(aa)); a3:=trunc(a*cos(tt));

a4:=trunc(a*sin(tt)); a5:=trunc(c*cos(qq)); a6:=trunc(c*sin(qq));

a7:=trunc(b*cos(dd)); a8:=trunc(b*sin(dd)); a9:=trunc(c*cos(aa));

a10:=trunc(c*sin(aa)); a11:=trunc(c*cos(aa));

a12:=trunc(c*sin(aa));

if (mm0)and(b>0)and(c>0)and(aa>0)and(aa0) and(dd<180) then begin

if (vv0) then begin

x:=-300;y:=0;xx:=x;yy:=y;

for j:=1 to 20 do begin

xx:=xx+a+a3+a5+a11; yy:=yy-a4-a6-a12;

for i:=1 to 10 do begin

xe:=x; ye:=y;

xa:=x+a; ya:=y;

xd:=x+a1; yd:=y-a2;

xc:=x+a1+a3; yc:=y-a2-a4;

xb:=x+a1+a3+a5; yb:=y-a2-a4-a6;

line(xa,ya,xb,yb);line(xb,yb,xc,yc);line(xc,yc,xd,yd);line(xd,yd,xe,ye);

line(xe,ye,xa,ya);

xe:=x+a+a1+a3+a5; ye:=y-a2-a4-a6;

xa:=x+a1+a3+a5; ya:=y-a2-a4-a6;

xd:=x+a+a3+a5; yd:=y-a4-a6;

xc:=x+a+a5; yc:=y-a6;

xb:=x+a; yb:=y;

line(xa,ya,xb,yb);line(xb,yb,xc,yc);line(xc,yc,xd,yd);line(xd,yd,xe,ye);

line(xe,ye,xa,ya);

xe:=x+a1+a3+a5+a7; ye:=y-a2-a4-a6-a8;

xa:=x+a1+2*a3+a5+a7; ya:=y-a2-2*a4-a6-a8;

xd:=x+a1+a3+a5; yd:=y-a2-a4-a6;

xc:=x+a+a1+a3+a5; yc:=y-a2-a4-a6;

xb:=x+a+a1+a3+a5+a9; yb:=y-a2-a4-a6-a10;

line(xa,ya,xb,yb);line(xb,yb,xc,yc);line(xc,yc,xd,yd);line(xd,yd,xe,ye);

line(xe,ye,xa,ya);

xd:=x+a; yd:=y;

xc:=x; yc:=y;

xe:=x+a-a7; ye:=y+a8;

xa:=x+a-a3-a7; ya:=y+a4+a8;

xb:=x-a11; yb:=y+a12;

line(xa,ya,xb,yb);line(xb,yb,xc,yc);line(xc,yc,xd,yd);line(xd,yd,xe,ye);

line(xe,ye,xa,ya);

x:=x+a-a1-a3-a7; y:=y+a2+a4+a8;

xe:=x; ye:=y;

xa:=x+a; ya:=y;

xd:=x+a1; yd:=y-a2;

xc:=x+a1+a3; yc:=y-a2-a4;

xb:=x+a1+a3+a5; yb:=y-a2-a4-a6;

line(xa,ya,xb,yb);line(xb,yb,xc,yc);line(xc,yc,xd,yd);line(xd,yd,xe,ye);

l ine(xe,ye,xa,ya);

xe:=x+a+a1+a3+a5; ye:=y-a2-a4-a6;

xa:=x+a1+a3+a5; ya:=y-a2-a4-a6;

xd:=x+a+a3+a5; yd:=y-a4-a6;

xc:=x+a+a5; yc:=y-a6;

xb:=x+a; yb:=y;

line(xa,ya,xb,yb);line(xb,yb,xc,yc);line(xc,yc,xd,yd);line(xd,yd,xe,ye);

line(xe,ye,xa,ya);

xe:=x+a1+a3+a5+a7; ye:=y-a2-a4-a6-a8;

xa:=x+a1+2*a3+a5+a7; ya:=y-a2-2*a4-a6-a8;

xd:=x+a1+a3+a5; yd:=y-a2-a4-a6;

xc:=x+a+a1+a3+a5; yc:=y-a2-a4-a6;

xb:=x+a+a1+a3+a5+a9; yb:=y-a2-a4-a6-a10;

line(xa,ya,xb,yb);line(xb,yb,xc,yc);line(xc,yc,xd,yd);line(xd,yd,xe,ye);

line(xe,ye,xa,ya);

e nd;

x:=xx; y:=yy;

end;

end else begin writeln('oshibka 1');goto 1;end;

end else begin writeln('oshibka 2');goto 1;end;

readln;

2:

closegraph;end.

Приложение 4

Пример 1.

vvedite

75 120 75 45 25

Пример 2.

vvedite

85 150 75 85 95

Характеристики

Список файлов курсовой работы