104351 (598205), страница 4
Текст из файла (страница 4)
Генеральная совокупность – однородная совокупность данных, по которой делаются выводы для принятия решения на основании результатов анализа выборки.
Данные, полученные на основании выборки – первичный статистический материал, на основании которого возможны обработка и анализ данных.
Например, решение о качестве партии продукции принимается на основании некоторой выборки, в пределах которой производятся измерения.
Таким образом, сбор данных – это не цель, а средство получения фактов, необходимых для принятия правильных решений.
Для упорядочения статистических данных можно произвести ранжирование, т.е. расположить полученные данные в порядке убывания или возрастания величин, а также подсчитать количество случаев регистрации одной и той же величины.
| Величина А | Случаи наблюдения величины А | N количество наблюдений величины А |
| ХХХ,Х | І І І І І | 5 |
| YYY,Y | І І | 2 |
| ZZZ,Z | I I I I I I I | 7 |
В полученном статистическом ряду величина N называется статистическим весом, или абсолютной частотой случайной величины, а данные в первом столбце – упорядоченным рядом случайной величины.
Изменения наблюдаемой величины могут быть дискретными и непрерывными.
Непрерывным называется такое изменение случайной величины, при котором находящиеся рядом значения в упорядоченном ряду этой величины отличаются на сколь угодно малую величину. Оно обычно может быть описано с помощью законов распределения Гаусса или Вейбулла.
Дискретным называется такое изменение случайной величины, при котором находящиеся рядом значения в упорядоченном ряду этой величины отличаются на некоторую конечную величину. Оно описывается биноминальным (гипергеометрическим) или пуассоновским законами.
Центральное значение интервала, его середина, называется величиной интервала, или его классом. Рекомендуется избегать слишком большого числа классов, т.к. при этом ряд может быть невыразительным. Проще оперировать рядами, в которых ширина классов одинакова.
Удобно представлять статистический материал числовыми значениями, отражающими в некоторой степени существенные характеристики статистического ряда – характеристики положения и рассеивания случайной величины. Важной характеристикой положения случайной величины является среднее арифметическое наблюдаемых значений. Оно является обобщающей характеристикой только в случае применения к однородной совокупности статистического материала.
Также существуют характеристики положения:
мода – наиболее часто встречающееся значение в ряду;
медиана – значение параметра, делящее упорядоченный ряд на две равные по объему части.
К характеристикам рассеивания относятся:
размах R – разница между наибольшим и наименьшим значениями величины;
выборочная дисперсия – величина, показывающая насколько тесно группируются значения вокруг средней арифметической или как они рассеиваются вокруг нее;
выборочное стандартное отклонение часто применяют вместо выборочной дисперсии;
коэффициент вариации – относительное колебание отдельных значений около средней арифметической.
Генеральную совокупность, как и выборочные данные, обычно представляют характеристиками положения (математическое ожидание) и рассеиванием случайной величины (дисперсия или стандартное отклонение).
Если число независимых случайных величин велико (приближается к бесконечности), среди них отсутствуют случайные величины с резко отличающимися от других случайных величин отклонениями, то распределение параметров качества будет стремиться к гаусовскому закону. При этом каждая из влияющих на качество величин может подчиняться любому другому закону распределения.
f
Если процесс отлажен и контролируем , то распределение значений параметра качества на каждой операции будет близко к гауссовскому.
Основной характеристикой является плотность распределения.
Площадь под кривой равна 1,0 или 100% всех значений случайной величины в генеральной совокупности.







95%

X
-3 -2 - M(x) - -2 -3
годность 99%

1. Контрольный листок
Какая бы задача не стояла перед системой, всегда первичным является сбор исходных данных.
Контрольный листок – инструмент для сбора данных и автоматического их упорядочения для облегчения дальнейшего их использования.
Он представляет собой заранее разработанный для конкретной цели бланк, с перечнем контролируемых параметров, в который в процессе сбора можно заносить информацию при помощи простых символов или пометок. Использование контрольных листков позволяет исключить переоформление и переписывание собранных данных.
| Причина брака | Количество случаев брака | Частота брака по конкретной причини (процент общего брака) |
| | ||
| | ||
| |
На контрольном листке должны быть указаны данные о том, кто, на каком этапе процесса, в течении какого времени собирал данные.
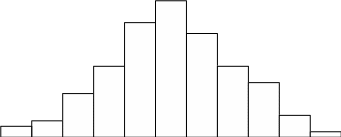
2. Гистограмма
Гистограммы, полигоны, кумулятивные кривые используются для обеспечения наглядности представления собранных данных.
Полигоны чаще используют для отображения дискретных изменений значений случайной величины.
Гистограмма распределения обычно строится для интервального изменения значения параметра.
Для построения гистограммы на интервалах на оси абсцисс строятся прямоугольники, высоты которых пропорциональны частотам интервалов. Сумма площадей столбиков равна 1,0.



При совмещении гистограммы и полигона, по мере увеличения количества измерений уменьшается ширина класса, и полигон превращается в кривую плотности распределения (штриховая кривая). Она имеет почти идеальную форму, к которой стремится реальный полигон, и похожа на кривую нормального распределения.
Кумулятивная (интегральная) кривая представляет собой график накопленных частот, получаемых для каждого значения при суммировании всех частот. Она строится как для дискретных, так и для непрерывных изменений значений параметров. Накопленные частоты относятся не к серединам интервалов, а к вершинным значениям каждого из них.
Для оценки соответствия качества процесса требованиям потребителя, гистограмму сравнивают с нанесенными на график полями допусков. Можно по расположению гистограммы по отношению к этим границам наглядно убедится в соответствии или несоответствии параметров качества процесса требованиям.
Если гистограмма имеет симметричную форму, можно предположить гауссовский закон распределения случайной величины. В таком случае среднее значение находится в центре размаха данных. Такой тип гистограмм называется обычным. Воспроизводимость процесса определяется исследованием постоянства следующих характеристик:
среднего значения (Х), математического ожидания (М(х)), стандартного отклонения.
Если брать в качестве границ допуска трехсигмовые пределы, которые часто используются на практике, то годными будут считаться 99,73% всех данных генеральной совокупности.
3. Диаграмма разброса
Диаграмма разброса – это инструмент, позволяющий определить вид и степень тесноты связи между соответствующими парами переменных данных.
Эти две переменные могут представлять собой две характеристики качества, два влияющих на характеристику качества фактора, или сочетание характеристики качества и фактора на нее влияющего.
Для построение диаграммы разброса необходимо:
-
Собрать необходимые парные данные (X,Y), желательно не менее 25-30 пар.
-
Определить max и min значения для обеих величин. Выбрать такие шкалы по осям графика, чтобы они были примерно одинаковыми. Проградуировать шкалы.
-
Начертить график и нанести на него все собранные данные. Следует определенным образом помечать точки, в которых значение величины наблюдаются несколько раз.
-
Сделать все необходимые обозначения: название диаграммы, интервал времени, число пар данных, названия и единицы измерения шкал, данные об исполнителе диаграммы.
При помощи диаграммы разброса можно наблюдать характер изменения параметров качества во времени при воздействии каких-либо факторов.
Y
90
80
70
60

Для определения общего распределения пар параметров по диаграмме рассеивания необходимо:
-
определить выбросы (далеко отстающие точки);
-
исключить эти точки из корреляционного анализа (на основании специальных критериев)
-
сравнить полученное скопление точек с возможными вариантами их расположения
-
сделать вывод о корреляции параметров.
n=25






50 60 70 80 Х
Возможные варианты расположения точек на диаграмме рассеивания и соответствующие им виды корреляции



Отсутствие корреляции
Прямая корреляция
Обратная корреляция










Криволинейная корреляция
Слабая прямая корреляция
Слабая обратная корреляция
















