183554 (596676), страница 2

Просмтор этого файла доступен только зарегистрированным пользователям. Но у нас супер быстрая регистрация: достаточно только электронной почты!

Текст из файла (страница 2)

В экономических задачах чаще встречаются задачи на условный экстремум. Перейдем к рассмотрению таких задач.

3. Задача математического программирования (ЗМП).

1. Общая постановка задачи

В теории экстремума на независимые переменные x₁,x_2, …,х_n не накладываются никакие дополнительные условия, т.е. не требуется, чтобы переменные удовлетворяли некоторым дополнительным ограничениям.

Рассмотрим другую задачу. Найти максимум (минимум) функции y=f(x₁,x_2, …,х_n), при условии, что независимые переменные x₁,x_2, …,х_n удовлетворяют системе ограничений:

g ₁(x₁,x_2, …,х_n) ≤b₁,

…………………………

g_m(x₁,x_2, …,х_n) ≤b_m,

g_m+1(x₁,x_2, …,х_n) ≥b_m+1,

…………………………

g_k(x₁,x_2, …,х_n) ≥b_k, (3.1)

g_k+1(x₁,x_2, …,х_n) =b_k+1,

…………………………

g_p(x₁,x_2, …,х_n) =b_p,

x₁,x_2,…,х_n ≥0.

Функцию y=f(x₁,x_2, …,х_n) принято называть целевой, т.к. её максимизация (минимизация) часто есть выражение какой-то цели, систему ограничений (3.1) – специальными ограничениями ЗМП, неравенства x₁≥0 ,x≥0_2, …, х_n≥0 – общими ограничениями ЗМП. Множество всех допустимых решений ЗМП (х_j≥0, j= ) называется допустимым множеством этой задачи.

Точка (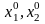 ) называется оптимальным решением для функции двух переменных, если, во-первых, она есть допустимое решение этой ЗМП, а во-вторых, на этой точке целевая функция достигает максимума (минимума) среди всех точек, удовлетворяющих ограничениям (3.1), причём

f (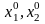 )≥ f(x₁,x₂)(в случае решения задачи на отыскание максимума),

f (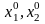 ) ≤ f(x₁,x₂) (в случае решения задачи на отыскание минимума).

Если в ЗМП все функции f(x₁,x_2, …,х_n), g_i(x₁,x_2, …,х_n) линейны, то имеем задачу линейного программирования (ЗЛП), если хотя бы одна из функций нелинейная, имеем задачу нелинейного программирования (ЗЛП). Рассмотрим ЗЛП.

2) ЗЛП и способы её решения.

ЗЛП имеет вид F=c₁x₁+c₂x₂+…+c_nx_n+c₀→min(max). При этом переменные должны удовлетворять ограничениям:

а ₁₁х₁+ а₁₂х₂+…+а_1nх_n≤b₁

…………………………

а_m1х₁+ а_m2х₂+…+a_mnx_n≤b_m

а_m+11х₁+ а_m+12х₂+…+а_m+1nх_n≥b_m+1

…………………………

а_k1х₁+ а_k2х₂+…+а_knх_n≥b_k (3.2)

а_k1+1х₁+ а_k+12х₂+…+а_k+1nх_n=b_k+1

………………………….

а_p1х₁+а_p2х₂+…+а_pnх_n=b_p

x₁,x_2,…,х_n ≥0.

ЗЛП может быть записана в различных формах:

Общий вид: найти минимум (максимум) целевой функции F при ограничениях (3.2) и условии неотрицательности переменных.

Стандартный вид: найти минимум (максимум) целевой функции F и ограничениях, заданных в виде неравенств и добавлены условия о неотрицательности переменных.

Канонический вид: вид, в котором нужно найти минимум (максимум) целевой функции F, где все ограничения заданы в виде равенств и есть условие неотрицательности переменных.

Стандартную задачу можно привести к каноническому виду, путём введения дополнительных неотрицательных переменных. Т.е. свести к системе m линейных уравнений с n переменными.

Любые m переменных системы m линейных уравнений с n переменными (m

Базисным решением системы m линейных уравнений с n переменными называют решение, в котором все m-n неосновных переменных равны нулю.

Для обоснования свойств ЗЛП и методов её решения, рассмотрим 2 вида записи канонической задачи.

1 вид – матричная форма записи: С=(c₁,c₂…c_n,c₀).

Х= А= В= (3.3)

F=CX→ min (max)

AX=B, X≥0

2 вид – векторная форма записи:

F=CX→ min (max)

р₁x₁+р₂x₂+…+р_nx_n=р. Х≥0.

р₁= р₂= … р _n= .

Для того чтобы рассмотреть теоретические основы метода линейного программирования, определим понятие выпуклого множества точек, дав ему определение в аналитической форме:

Множество точек является выпуклым, если оно вместе с любыми своими двумя точками содержит их произвольную линейную комбинацию. Точка Х является выпуклой линейной комбинацией точек Х₁, Х₂, … Х_n, если выполняются условия Х= α₁x₁+α₂x₂+…+α_nx_n, α_j≥0, (j=1,…,n), .

Теорема 1. Выпуклый линейный многогранник является выпуклой линейной комбинацией своих угловых точек. (Примем без доказательства).

Теорема 2. Множество всех допустимых решений системы ограничений ЗЛП является выпуклым.

□ Пусть Х₁=( x ,x _, …,х ) и Х₂=( x ,x _, …,х )- два допустимых решения задачи (3.3), заданной в матричной форме. Тогда АХ₁=В и АХ₂=В. рассмотрим выпуклую линейную комбинацию решений Х₁ и Х₂ , т.е. Х=α₁Х₁+α₂Х₂ при α₁ ≥0, α₂ ≥0 и α₁+α₂=1. Покажем, что она также является допустимым решением системы АХ=В. В самом деле, АХ=А(α₁Х₁+α₂Х₂)=α₁АХ₁+(1-α₁)АХ₂= α₁В+(1-α₁)В=В, т.е. решение удовлетворяет системе ограничений. Но т.к. Х₁≥0, Х₂ ≥0, α₁ ≥0, α₂ ≥0 , то и Х ≥0, т.е. решение Х удовлетворяет условию (3.3). ■

Итак, доказано, что множество всех допустимых решений ЗЛП является выпуклым, которое будем называть многогранником решений.

Ответ на вопрос, в какой точке многогранника решений возможно оптимальное решение ЗЛП, даёт следующая теорема.

Теорема 3. Если ЗЛП имеет оптимальное решение, то линейная функция F принимает максимальное (минимальное) значение в одной из угловых точек многогранника решений. Если линейная функция принимает максимальное значение более чем в одной угловой точке, то она принимает его в произвольной точке, являющейся выпуклой линейной комбинацией этих точек.

□ Будем полагать, что многогранник решений является ограниченным. Обозначим его угловые точки через Х₁,Х_2, …,Х_n , а оптимальное решение через Х^*. Тогда F(Х^*) ≥F(X), для всех точек многогранника решений. Если Х^* угловая, то первая часть теоремы доказана. Предположим, что Х^* не является угловой точкой, тогда Х^*, на основании теоремы 1, можно представить как выпуклую линейную комбинацию угловых точек многогранника решений, т.е. Х^*=α₁x₁+α₂x₂+…+α_рx_р, α_j≥0, (j=1,…,n), . Т.к.

F(Х^*)=F(α₁x₁+α₂x₂+…+α_рx_р)=α₁F(x₁)+α₂F(x₂)+…+α_рF(x_р). (3.4)

В этом выражении среди значений F(X_j)(j=1,2,…,p) выберем максимальное. Обозначим его через М, т.е. М=max F(X_j). Тогда

α₁F(x₁)+ α₂F(x₂) +…+ α_рF(x_р)≤ α₁М+ α₂М +…+ α_рМ = М(α₁+α₂+…+α_р) =М.

Значит F(Х^*)≤М. Пусть М=F(X_k), т.е. соответствует угловой точке X_k (1≤к≤р).

Тогда F(Х^*) ≤ F(X_k). Но по предположению Х^* - оптимальное решение, поэтому F(Х^*)≥F(X_k)=М, следовательно, F(Х^*)=М=F(X_k), где X_k- угловая точка. Итак, существует угловая точка X_k, в которой линейная функция принимает максимальное значение.

Для доказательства второй части теоремы допустим, что F(Х) принимает максимальное значение более чем в одной угловой точке, например в точках Х₁, Х₂, … Х_q , где 1≤ q ≤ р; тогда F(Х₁)=F(Х₂)=…=F(Х_n)=M.

Пусть Х выпуклая линейная комбинация этих угловых точек, т.е. Х= α₁Х₁+α₂Х₂+ …+α_qХ_q , α_j≥0, (j=1,…,q), . В этом случае, учитывая, что функция F(Х) – линейная, получим F(Х)=F(α₁Х₁+α₂Х₂+…+α_qХ_q)=α₁F(Х₁)+ +α₂F(Х₂)+…+α_qF(Х_q)=α₁M+α₂M+…+α_qM=M =M, т.е. линейная функция F принимает максимальное значение в произвольной точке Х, являющейся выпуклой линейной комбинацией угловых точек Х₁, Х₂, … Х_q ■

Замечание. Требование ограниченности многогранника решений в теореме является существенным, т.к. в случае неограниченной многогранной области не каждую точку можно представить выпуклой линейной комбинацией её угловых точек.

Доказанная теорема является фундаментальной, т.к. она указывает принципиальный путь решения ЗЛП.

Рассмотрим геометрический метод решения ЗЛП в случае функции двух переменных.

Было доказано, что оптимальное решение ЗЛП находится, по крайней мере, в одной из угловых точек многогранника решений.

Рассмотрим задачу в стандартной форме с двумя переменными.

F=c₁x₁+c₂x₂+с₀ →min(max),

П ри ограничениях а₁₁х₁+ а₁₂х₂ ≤b₁,

а₂₁х₁+ а₂₂х₂ ≤b₂,

………………

a_n1х₁+ а_n2х₂≤b_n ,

при условии, что x₁ ≥0 ,x₂ ≥0 .

Пусть геометрическим изображением системы ограничений является многоугольник ABCDE. Необходимо среди точек этого многоугольника найти такую точку, в которой линейная функция F=c₁x₁+c₂x₂+с₀ принимает максимальное (или минимальное) значение. Рассмотрим линии уровня функции F или

c ₁x₁+c₂x₂=С ( 3.5).

Это уравнение прямой. Линии уровня функции F параллельны, т.к. их угловые коэффициенты определяются только соотношением между коэффициентами c₁ и c₂ и, следовательно, равны. Т.о., линии уровня функции F – это своеобразные «параллели», расположенные обычно под углом к осям координат.

Важное свойство линий уровня линейной функции состоит в том, что при параллельном смещении линии в одну сторону уровень только возрастает, а при смещении в другую сторону – только убывает. При фиксированном С рассмотрим линейную функцию. Чем больше значение С, тем больше значение линейной функции. Определив направление возрастания линейной функции, найдём точку, принадлежащую многоугольнику, в которой функция принимает максимальное или минимальное значение.

Геометрическим изображением системы ограничений может служить и многоугольная область. Рассмотрим следующую задачу.

1.В суточный рацион включают два продукта питания П₁ и П₂, причём продукта П₁ должно войти в дневной рацион не более 200 ед. Стоимость питательных веществ в 1 ед. продукта, минимальные нормы потребления указаны в таблице. Определить оптимальный рацион питания, стоимость которого будет наименьшей.

Питательные вещества		Минимальная норма потребления		Содержание питательных веществ в 1 ед. продукта.
				П1		П1
А В	120 160		0,2 0,4		0,2 0,2

Решение.

Обозначим х₁ – количество продукта питания П₁,

х₂ – количество продукта питания П₂.

F=2 х₁ +4 х₂ →min. (суммарная стоимость) При ограничениях

х₁ ≤ 200,

0,2 х₁ +0,2 х₂ ≥120,

0,4 х₁ +0,2 х₂ ≥160.

Г рафическим решением системы ограничений является множество точек плоскости, называемое областью допустимых решений (ОДР). Линии уровня 2х₁+4х₂=0 х₂=- х_1.

Получаем, что минимальное значение, при заданных ограничениях на переменные, достигается в точке А(200;400). F(A)=2000.

Ответ: наименьшая стоимость 2000 будет при рационе 200 ед. продукта П₁ и 400 ед. продукта П₂.

Не всегда бывает единственное оптимальное решение. Рассмотрим другую задачу.

2. F=4x₁+4x₂ →max. При ограничениях

2x₁+x₂ ≥7,

x₁-2x₂ ≥-5,

x₁+x₂≤14,

2x₁-x₂ ≤18.

Решив, систему ограничений найдём ОДР. Линия уровня будет иметь вид 4x₁+4x₂=0 x₂=-x₁.

В данной задаче линия уровня с максимальным уровнем совпадает с граничной линией многоугольника решений. Найдём точку пересечения линии II с линией III:

х₁= .

Найдём точку пересечения линии III с линией IV: 14- х₁=2 х₁-18. Отсюда х₁= . Следовательно, х₁=c, x₂=14-c, c [ ; ]. Пусть х₁=9 [ ; ], х₂=5.

F=4·9+4·5=56.

Ответ: F_max=56 при множестве оптимальных решений х₁=c, x₂=14-c, где c [ ; ].

Рассмотренный геометрический метод решения ЗЛП обладает рядом достоинств. Он прост, нагляден, позволяет быстро и легко получить ответ.

Однако есть и недостатки. Возникают «технические» погрешности, которые неизбежно возникают при приближенном построении графиков. Второй недостаток геометрического метода заключается в том, что многие величины, имеющие чёткий экономический смысл (например, такие, как остатки ресурсов производства), не выявляются при геометрическом решении задач. Его можно применять только в том случае, когда число переменных в стандартной задаче равно двум. Поэтому необходимы аналитические методы, позволяющие решать ЗЛП с любым числом переменных и выявить экономический смысл, входящих в них величин.

Одним их таких методов является симплексный метод.

В данном пункте была рассмотрена теорема, из которой следует, что если ЗЛП имеет оптимальное решение, то оно соответствует хотя бы одной угловой точке многогранника решений. Поэтому решение ЗЛП может быть следующим: перебрать конечное число всех угловых точек многогранника решений и выбрать среди них ту, на которой функция цели принимает оптимальное решение. Однако, практическое осуществление такого перебора связано с трудностями, т.к. число решений может быть чрезвычайно велико.

П усть ОДР изображается многоугольником ABCDEGH. Предположим,

что его угловая точка соответствует исходному допустимому решению. При беспорядочном наборе пришлось бы перебирать все 7 угловых точек многогранника. Однако, из чертежа видно, что после вершины А выгодно перейти к соседней вершине В, а затем – к оптимальной точке С. Вместо семи перебрали 3 вершины, последовательно улучшая линейную функцию.

Идея последовательного улучшения решения легла в основу универсального метода решения ЗЛП – симплексного метода. Для использования симплексного метода ЗЛП должна быть приведена к каноническому виду. Для реализации симплексного метода необходимо освоить 3 основных элемента:

• способ определения какого – либо первоначального допустимого решения

• правило перехода к лучшему решению

• критерий проверки оптимальности найденного решения.

Алгоритм конкретной реализации этих элементов рассмотрим на примере.

Практические расчёты при решении реальных задач симплексным методом выполняются в настоящее время с помощью компьютера, однако, если расчёты выполняются без ЭВМ, то удобно использовать симплексные таблицы.

Алгоритм составления симплексных таблиц:

1. Система ограничений приводится к каноническому виду.

Для нахождения первоначального базисного решения переменные разбиваются на основные и неосновные. Т.к. определитель, составленный из коэффициентов при дополнительных переменных отличен от нуля, то эти переменные можно взять в качестве основных. При выборе основных переменных не обязательно составлять определитель, достаточно воспользоваться следующим правилом: в качестве основных переменных следует выбрать такие, каждая из которых входит только в одно из уравнений системы ограничений, при этом нет таких уравнений системы, в которые не входит ни одна из этих переменных.

1. Составляют таблицу, где в последней строке указываются коэффициенты функции с противоположным знаком. В левом столбце таблицы записывают основные переменные, в первой строке – все переменные, в последнем столбце свободные члены системы.

1. Проверяют выполнение критерия оптимальности – наличие в последней строке отрицательных коэффициентов. Если таких нет, то решение оптимально, достигнут, например, максимум функции (в правом нижнем углу таблицы), основные переменные при этом принимают значение b_i, а неосновные переменные равны нулю, т.е. получается оптимальное базисное решение.

2. Если критерий оптимальности не выполнен, то наибольший по модулю отрицательный коэффициент в последней строке определяет разрешающий столбец S. Составляют оценочные ограничения по следующим правилам:

   • ∞, если b_i и а_is имеют разные знаки;

   • ∞, если b_i=0 и а_is<0;

   • ∞, если а_is=0;

   • 0, если b_i=0 и а_is>0;

   • , если b_i и а_is имеют одинаковые знаки.

Определяют min . Если конечного минимума нет, то задача не имеет конечного оптимума. Далее выбирают строку с номером q, на которой он достигается (любую, если их несколько), и называют её разрешающей строкой. На пересечении разрешающей строки и разрешающего столбца находится разрешающий элемент а_qs.

1. Переходим к следующей таблице по правилам:

а) в левом столбце записывают новый базис: вместо основной переменной х_q - переменную х_s, а геометрически произойдёт переход к соседней вершине многоугольника, где значение линейной функции «лучше». Значение линейной функции увеличится, т.к. переменная, входящая в выражение функции, станет основной, т.е. будет принимать не нулевое, а положительное значение;

1. новую строку с номером q получают из старой делением на разрешающий элемент а_qs;

2. все остальные элементы вычисляют по правилу многоугольника:

;

Далее переходим к пункту 3 алгоритма.

Замечание: при отыскании минимума функции Z, полагаем, что F=-Z и учитываем, что Z_min=-F_max.

Решим задачу симплексным методом.

Для производства трёх изделий А,В и С используются три вида ресурсов. Каждый из них используется в объёме, не превышающем 180, 210 и 236 кг. Нормы затрат каждого из видов ресурсов на одно изделие и цена единицы изделий приведены в таблице.

Вид ресурса	Нормы затрат ресурсов на 1 изделие, кг
	А	В	С
1 2 3	4 3 1	2 1 2	1 3 5
Цена изделия, у.е.	10	14	12

Определить план выпуска изделий, обеспечивающий получение оптимального дохода.

Решение. х₁- количество выпускаемых изделий А

х₂- количество выпускаемых изделий В

х₃- количество выпускаемых изделий С.

Т огда целевая функция будет иметь вид: F=10x₁+14x₂+12 х₃ →max

при ограничениях: 4x₁+2x₂+х₃≤180

3x₁+x₂+3х₃≤210

x₁+2x₂+5х₃≤236

Приведём систему к каноническому виду:

4 x₁+2x₂+х₃+х₄=180

3x₁+x₂+3х₃+х₅=210

x₁+2x₂+5х₃+х₆=236.

Составляем таблицу

	х1	х2	х3	х4	х5	х6	Свободный член
х4 х5 х6	4 3 1	2 1 2	1 3 5	1 0 0	0 1 0	0 0 1	180 210 236
F’	-10	-14	-12	0	0	0	0

Определим ведущий элемент: min . Далее выполняем действия, следуя алгоритму.

	х1	х2	х3	х4	х5	х6	Свободный член
х2 х5 х6	2 1 -3	1 0 0	1/2 5/2 4	1/2 -1/2 -1	0 1 0	0 0 1	90 120 56
F’	18	0	-5	7	0	0	1260

min

	х1	х2	х3	х4	х5	х6	Свободный член
х2 х5 х3	19/8 23/8 -3/4	1 0 0	0 0 1	5/8 1/8 -1/4	0 1 0	-1/8 -5/8 1/4	83 85 14
F’	54/4	0	0	23/4	0	5/4	1330

Ответ: Чтобы получить оптимальный доход, нужно выпускать 83 ед. изделия В, 14 ед. изделия С, а изделие А не выпускать. Оптимальный доход составит 1330 у.е. По решению задачи видим, что у предприятия остаются свободными 85 кг. второго вида ресурсов, 1 и 3 вид полностью расходуются [5]

3) Двойственная задача.

Каждой задаче линейного программирования соответствует другая задача, называемая двойственной или сопряжённой по отношению к исходной. Теория двойственности полезна для проведения качественных исследований ЗЛП. В главе I пункте 2) рассмотрена задача об использовании ресурсов. Предположим, что некоторая организация решила закупить ресурсы и необходимо установить оптимальные цены на эти ресурсы y_1,y₂,y₃. Очевидно, что

покупающая организация заинтересована в том, чтобы затраты на все ресурсы Z в количествах 180, 210, 236 по ценам соответственно y_1,y₂,y₃ были минимальными, т.е. Z= 180y₁+210y₂+236y₃→min. С другой стороны, предприятие, продающее ресурсы, заинтересовано в том, чтобы полученная выручка была не мене той суммы, которую предприятие может получить при переработке ресурсов в готовую продукцию. На изготовление единицы продукции А расходуется 4кг. ресурса 1, 3кг. ресурса 2, 1кг. ресурса 3 по цене соответственно y_1,y₂,y₃. Поэтому, для удовлетворения требований продавца затраты на ресурсы, потребляемые при изготовлении единицы продукции, должны быть не менее её цены 10у.е., т.е. 4 y₁+3 y₂+ y₃≥10.

Аналогично можно составить ограничения в виде неравенств по каждому виду продукции. Экономико-математическая модель исходной задачи и полученной двойственной задачи приведены в таблице.

Обе задачи, представленные в таблице обладают следующими свойствами:

1. В одной задаче ищут максимум линейной функции, в другой минимум.

2. Коэффициенты при переменных в линейной функции одной задачи являются свободными членами системы ограничений в другой.

3. Каждая из задач задана в стандартной форме, причём в задаче максимизации – все неравенства вида «≤ », а в задаче минимизации – все неравенства вида «≥ ».

4. Матрицы коэффициентов при переменных в системах ограничений обеих задач являются транспонированными друг к другу.

Для задачи I А= , для задачи II А =

1. Число неравенств в системе ограничений одной задачи совпадает с числом переменных в другой задаче.

2. Условия неотрицательности переменных имеются в обеих задачах.

Две задачи I и II линейного программирования, обладающие указанными свойствами, называются симметричными взаимодвойственными задачами.

Исходя из определения, можно предложить следующий алгоритм составления двойственной задачи.

1. Приводят все неравенства системы ограничений исходной задачи к одному смыслу: если в исходной задач ищут максимум линейной функции, то все неравенства системы ограничений приводят к виду «≤ », а если минимум – к виду «≥ ».

2. Составляют расширенную матрицу системы А₁, в которую включают матрицу коэффициентов при переменных, столбец свободных членов системы ограничений и строку коэффициентов при переменных в линейной функции.

3. Находят матрицу А , транспонированную к матрице А₁.

4. Формулируют двойственную задачу на основании полученной матрицы А и условия неотрицательности переменных.

Связь между оптимальными решениями двойственных задач устанавливается с помощью теорем двойственности. Вначале рассмотрим вспомогательное утверждение.

Основное неравенство теории двойственности. Пусть имеется пара двойственных задач I и II. Покажем, что для любых допустимых решений Х= (x₁,x_2, …,х_n) и У=(y_1,y₂,…,y_m)исходной и двойственной задачи справедливо неравенство F(X) ≤ Z(Y) или ≤ (3.6)

□ Возьмём неравенства системы ограничений исходной задачи ≤b_i и умножим соответственно на переменные y_1,y₂,…,y_m и, сложив правые и левые части полученных неравенств, имеем

≤ . (3.7)

Аналогично умножаем систему ограничений двойственной задачи на переменные x₁,x_2, …,х_n , получим

≥ (3.8)

Т.к. левые части неравенств (3.7) и (3.8) представляют одно и тоже выражение у_j, то в силу транзитивности неравенств получим доказываемое неравенство (3.6).■

Теперь докажем признак оптимальности решений.

Достаточный признак оптимальности.

Если X^*=(x , x ,…, x ) и У^*=(у , у ,…, у ) – допустимые решения взаимно двойственных задач, для которых выполняется равенство

F(X^*) =Z(Y^*) (3.9)

то Х^* оптимальное решение исходной задачи I, а У^* - двойственной задачи II.

□ Пусть Х₁ любое допустимое решение исходной задачи I. Тогда на основании основного неравенства (3.6) получим F(X₁) ≤ Z(Y^*). Однако Х₁ - произвольное решение задачи I. Аналогично доказывается, что решение У^* оптимально для задачи II.■

Всегда ли для каждой пары двойственных задач есть одновременно оптимальные решения; возможны ли ситуации, когда одна из двойственных задач имеет решение, а другая нет?

Ответ на эти вопросы даёт следующая теорема.

Первая (основная) теорема двойственности. Если одна из взаимно двойственных задач имеет оптимальное решение, то его имеет и другая, причём оптимальные значения их линейных функций равны:

F_max=Z_min или F(X^*) =Z(Y^*) (3.10)

Если линейная функция одной из задач не ограничена, то система ограничений другой задачи противоречива.

Из первой части утверждения теоремы следует, что равенство (3.9) является не только достаточным, но и необходимым признаком оптимальности взаимно двойственных задач.

□ Докажем утверждение второй части методом от противного. Предположим, что в исходной задаче линейная функция не ограничена, т.е. F_max=∞, а условия двойственной задачи не являются противоречивыми, т.е. существует хотя бы одно допустимое решение У=(y_1,y₂,…,y_m). Тогда в силу основного неравенство теории двойственности (3.6) F(X) ≤ Z(Y), что противоречит условию неограниченности F(X). Следовательно, при F_max=∞ в исходной задаче, допустимых решений в двойственной задаче быть не может. ■

Экономический смысл первой теоремы двойственности состоит в следующем: план производства X^*=(x , x ,…, x ) и набор цен ресурсов У^*=(у , у ,…, у ) оказываются оптимальными тогда и только тогда, когда прибыль от продукции, найденная при ценах с₁, с₂,…, с_n,«внешних» (известных заранее), равна затратам на ресурсы по «внутренним»(определяемым только из решения задачи) ценам y_1,y₂,…,y_m . Для всех же других планов Х и У обеих задач в соответствии с основным неравенством (3.6) теории двойственности прибыль (выручка) от продукции всегда меньше (или равна) затрат на ресурсы.

Экономический смысл первой теоремы двойственности можно интерпретировать и так: предприятию безразлично, производить ли продукцию по оптимальному плану X^*=(x , x ,…, x ) и получать максимальную прибыль F_max либо продавать ресурсы по оптимальным ценам У^*=(у , у ,…, у ) и возместить от продажи равные ей минимальные затраты на ресурсы Z_min.

Связь между двумя взаимно двойственными задачами проявляется не только в равенстве оптимальных значений их линейных функций.

Пусть даны две взаимно двойственные задачи I и II. Если каждую из них решать симплексным методом, то необходимо привести их к каноническому виду, для чего в систему ограничений задачи I следует ввести m неотрицательных переменных x_n+1, x_n+2, … , x_n+m, а в систему ограничений задачи II - n неотрицательных переменных y_m+1, y_m+2,…,y_m+n. Системы ограничений двойственных задач примут вид:

+x_n+i=b_i, i=1,…,m (3.11) -y_m+j=c_j, j=1,…,n (3.12).

установим соответствие между первоначальными переменными одной из двойственных задач и дополнительными переменными другой задачи.

Теорема. Положительным (ненулевым) компонентам оптимального решения одной из взаимно двойственных задач соответствуют нулевые компоненты оптимального решения другой задачи, т.е. для любых i=1,2,…,m и j=1,2,…,n: если >0, то =0; если >0, то =0, и аналогично, если >0, то =0; если >0, то =0.

□ Выразим дополнительные переменные из системы ограничений (3.11) исходной задачи I и (3.12) двойственной задачи, представленных в каноническом виде:

x_n+i=b_i- , i=1,2,…,m (3.13)

y_m+j= -c_j, j=1,…,n. (3.14)

Умножая каждое равенство системы (4.9) на соответствующие переменные у_j≥0 и складывая полученные равенства, найдём

x_n+iy_i= b_iy_i- y_i (3.15)

Аналогично, умножая каждое неравенство системы (4.10) на соответствующие переменные x_j≥0 и складывая полученные равенства, найдём

y_m+j= y_i- c_j . (3.16)

Равенства (4.11)и(4.12) будут справедливы для любых допустимых значений переменных, в том числе и для оптимальных значений , , , . В силу первой теоремы двойственности (3.10) F(X^*) =Z(Y^*) или = , поэтому из записи правых частей равенств (3.15) и (3.16) следует, что они должны отличаться только знаком. С другой стороны, из неотрицательности выражений x_n+i y_i и y_m+j, входящие в выражения (3.15) и (3.16), следует, что правые части этих равенств должны быть неотрицательны.

Эти условия могут выполняться одновременно только при равенстве этих правых частей для оптимального значения переменных нулю:

=0,

=0. (3.17)

В силу условия неотрицательности переменных каждое из слагаемых в равенстве (4.13) должно равняться нулю:

=0, i=1,2,…,m

=0, j=1,2,…,n

Откуда и вытекает заключение теоремы. ■

Из доказанной теоремы следует, что введённое ранее соответствие между переменными двойственных задач представляет соответствие между основными (как правило не равными нулю) переменными одной из двойственных задач и неосновными (равными нулю) переменными другой задачи, когда они образуют допустимые базисные решения.

Рассмотренная теорема является следствием следующей теоремы.

Вторая теорема двойственности. Компоненты оптимального решения двойственной задачи равны абсолютным значениям коэффициентов при соответствующих переменных линейной функции исходной задачи, выраженной через неосновные переменные её оптимального решения.

Метод, при котором вначале симплексным методом решается двойственная задача, а затем оптимум и оптимальное решение исходной задачи находятся с помощью теорем двойственности, называется двойственным симплексным методом. Этот метод бывает выгодно применять, когда первое базисное решение исходной задачи недопустимое или, например, когда число её ограничений m больше числа переменных n.

С помощью теорем двойственности найдём решение задачи II. Получаем следующий набор цен ресурсов ( ), при котором минимальные затраты составят 1330. [5]

4) Задача нелинейного программирования. (ЗНП)

Рассмотрим ЗНП и способы её решения. Математическая модель ЗНП в общем виде формулируется следующим образом:

f =(x₁,x_2, …,х_n) → min (max). При этом переменные должны удовлетворять ограничениям:

g ₁(x₁,x_2, …,х_n) ≤b₁,

…………………………

g_m(x₁,x_2, …,х_n) ≤b_m,

g_m+1(x₁,x_2, …,х_n) ≥b_m+1,

…………………………

g_k(x₁,x_2, …,х_n) ≥b_k,

g_k+1(x₁,x_2, …,х_n)=b_k+1,

………………………

g_p(x1,x_2, …,х_n)=b_p.

x₁,x_2,…,х_n ≥0, где хотя бы одна из функций f, g_i нелинейная.

Для ЗЛП нет единого метода решения. В зависимости от вида целевой функции и системы ограничений разработаны специальные методы решения, к которым относятся метод множителей Лагранжа, градиентные методы, приближённые методы решения, графический метод.

Рассмотрим основные идеи графического метода.

Максимум и минимум достигается в точках касания линии уровня с областью допустимых решений (ОДР), которая задается системой ограничений. Например, если линии уровня - прямые, то точки касания можно определить, используя геометрический смысл производной.

Рассмотрим на примерах решение ЗНП.

1. Найти экстремумы функции L(x₁,x₂)=x₁+2x₂ при ограничениях

, .

Р

5

ешение. ОДР – это часть круга с радиусом 5, расположенная в I четверти. Найдём линии уровня функции L: x₁+2x₂=C. Выразим x₂= . Линиями уровня будут параллельные прямые с угловым коэффициентом, равным - . Минимум функции достигается в точке (0;0), L_min=0, т.к. градиент (1,2) направлен вверх вправо. Максимум достигается в точке касания кривой х₂= и линии уровня. Т.к. угловой коэффициент касательной к графику функции равен - , найдём координаты точки касания, используя геометрический смысл производной.

=- ; ( ) =- ;

=- ; x₀= ; x₂=2 .

Тогда L= +2∙2 =5 .

Ответ: Минимум достигается в точке О(0;0), глобальный максимум, равный 5 , в точке А( ;2 ) .

2. Найти экстремумы функции L=(x₁-6)²+(x₂-2)² при ограничениях

x₁+x₂≤8

3 x₁+x₂ ≤15

x₁+x₂ ≥1

.

Р ешение. ОДР – многоугольник ABCDE. Линии уровня представляют собой окружности (x₁-6)²+(x₂-2)²=С с центром в точке О₁(6;2). Возьмём, например, С=36, видим, что максимум достигается в точке А(0;4), которая лежит на окружности наибольшего радиуса, пересекающую ОДР. L(A)=(0-6)²+(4-2)²=40. Минимум - в точке F, находящейся на пересечении прямой 3x₁+x₂ =15 и перпендикуляра к этой прямой, проведённого из точки О₁. Т.к. угловой коэффициент равен -3, то угловой коэффициент перпендикуляра равен . Из уравнения прямой, проходящей через данную точку О₁ с угловым коэффициентом , получим (x₂-2)= (x₁-6). Найдём координаты точки Е

х ₁-3х₂=0

3 x₁+x₂ =15.

Решив систему, получаем Е(4.5; 1.5).

L (E) = (4.5-6)²+ (1.5-2)²=2.5.

Ответ: Минимум, равный 2.5 достигается в точке (4.5; 1.5), максимум, равный 40, в точке (0;4).

3. Найти экстремумы функции L=(x₁-1)²+(x₂-3)²

при ограничениях , .

Р ешение: ОДР является часть круга, с центром в начале координат, с радиусом 5, расположенная в I четверти. Линии уровня – это окружности с центром в точке О₁ и радиуса С, т.к. (x₁-1)²+(x₂-3)²=С. Точка О₁ – это вырожденная линия уровня, соответствующая минимальному значению С=0. глобальный максимум достигается в точке А, лежащей на пересечении ОДР с линией уровня наибольшего радиуса. При этом

Характеристики

Список файлов ВКР