4 -4 (1039348), страница 2
Текст из файла (страница 2)
 . (1.5)
. (1.5)
Соответственно, мощность вторичного излучения цели
 . (1.6)
. (1.6)
Если бы цель была изотропным вторичным излучателем, т. е рассеивала падающую энергию равномерно во всех угломестных направлениях, то плотность потока мощности на расстоянии  у РЛС была бы равна
у РЛС была бы равна  . С учетом же направленных свойств цели
. С учетом же направленных свойств цели
 . (1.7)
. (1.7)
Это произведение имеет размерность площади и характеризует, какую часть энергии падающей радиоволны получает цель, потери энергии во вторичном излучателе, направленные свойства вторичного излучения.
Тогда, подставляя (1.4), (1.5), (1.6), (1.7) в (1.2), окончательно получим
 , (1.8)
, (1.8)
где  - характеризует геометрические свойства цели,
- характеризует геометрические свойства цели,  - свойство цели избирательно отражать энергию в определенных угловых направлениях (анизотропность). Так как величина
- свойство цели избирательно отражать энергию в определенных угловых направлениях (анизотропность). Так как величина  зависит от соотношения размеров цели и длины волны падающего излучения, то и ЭПР цели косвенно зависит от этих же факторов.
зависит от соотношения размеров цели и длины волны падающего излучения, то и ЭПР цели косвенно зависит от этих же факторов.
Из формулы (1.2), получаем общее выражение для ЭПР:
 . (1.9)
. (1.9)
Для практического использования преобразуем формулу (1.9). Плотность потока мощности  , где E и H – амплитуды напряженностей электрического и магнитного полей в дальней зоне, связанные соотношением
, где E и H – амплитуды напряженностей электрического и магнитного полей в дальней зоне, связанные соотношением  , где
, где  - волновое сопротивление свободного пространства;
- волновое сопротивление свободного пространства;  - магнитная и электрическая постоянные. Поэтому
- магнитная и электрическая постоянные. Поэтому

 (1.10)
(1.10)
ЭПР является функцией направления облучения и характеризуется диаграммой вторичного излучения цели по мощности. Обычно ЭПР, представляемую в виде зависимости  , называют диаграммой обратного рассеяния (ДОР).
, называют диаграммой обратного рассеяния (ДОР).
Зависимость  имеет сложную, многолепестковую форму, обусловленную интерференцией излучения совокупности элементов реальной цели. Ширина лепестков зависит от отношения линейных размеров цели к длине волны, а ее оценка может быть произведена по формуле
имеет сложную, многолепестковую форму, обусловленную интерференцией излучения совокупности элементов реальной цели. Ширина лепестков зависит от отношения линейных размеров цели к длине волны, а ее оценка может быть произведена по формуле
 ,
,
где  - эквивалентный размер цели. Чем короче длина волны, тем уже лепестки диаграммы обратного вторичного излучения.
- эквивалентный размер цели. Чем короче длина волны, тем уже лепестки диаграммы обратного вторичного излучения.

Рисунок 1.2. ДОР самолета в горизонтальной плоскости при  =10 см(а) и
=10 см(а) и  =5 м(б)
=5 м(б)
На рисунке 1.2 представлены ДОР аэродинамических целей (самолетов), снятых при  =10 см и
=10 см и  =3-5 м. Из рисунка 1.2 видно, что мощность отраженного сигнала существенно зависит от ракурса наблюдения цели и длины волны. С направления 00 сигнал, принимаемый РЛС, будет достаточно мощным, а с направления 450 может быть близким к нулю. Уровень изменения сигнала, обусловленный флюктуациями ЭПР цели при изменении ракурса наблюдения, может достигать 40 Дб на сантиметровых волнах.
=3-5 м. Из рисунка 1.2 видно, что мощность отраженного сигнала существенно зависит от ракурса наблюдения цели и длины волны. С направления 00 сигнал, принимаемый РЛС, будет достаточно мощным, а с направления 450 может быть близким к нулю. Уровень изменения сигнала, обусловленный флюктуациями ЭПР цели при изменении ракурса наблюдения, может достигать 40 Дб на сантиметровых волнах.
Зависимость  для реальных целей сложной формы определяют экспериментально, либо рассчитывают специальными методами.
для реальных целей сложной формы определяют экспериментально, либо рассчитывают специальными методами.
Наиболее прямой способ получения сведений об ЭПР состоит в измерении радиолокационного отражения от самой цели или от точно выполненной ее модели. При этом измерения производят либо на специальных радиолокационных полигонах, либо в полевых условиях.
Для экспериментального определения ДОР цель перемещают вокруг РЛС и при этом измеряют напряженность поля  (Рисунок 1.3, а). Затем испытываемую цель
(Рисунок 1.3, а). Затем испытываемую цель



Передатчик
Приемник
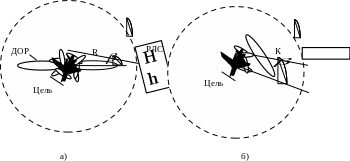
Рисунок 1.3. Условия экспериментального определения ДОР и ДР
заменяют эталонной (имеющей обычно форму шара) с известным значением ЭПР  и определяют напряженность поля
и определяют напряженность поля  . Так как параметры
. Так как параметры  и
и  не изменяются, то из выражения (1.8) находим искомое значение ЭПР:
не изменяются, то из выражения (1.8) находим искомое значение ЭПР:
 . (1.11)
. (1.11)
Средние значения ЭПР реальных целей приведены в таблице.
| Цель | бц, м2 | Цель | бц, м2 |
| Истребитель | 1...5 | Крылатая ракета | 0,1... 0,3 |
| Бомбардировщик | 7. ..20 | Автомобиль, танк | 7.. .30 |
| Транспортный самолет | 50... 150 | Большой корабль | >20000 |
| Ракета | 10.. .15 | Человек | 0,8...1 |
-
Дальность действия РЛС в свободном пространстве
Дальность действия РЛС это одна из основных тактических характеристик радиолокационных станций, которая определяет максимальное расстояние от РЛС  , в пределах которого она способна вести наблюдение за целями.
, в пределах которого она способна вести наблюдение за целями.
Дальность действия зависит от назначения РЛС. Так, например, у некоторых радиолокационных станций для слежения за баллистическими ракетами она может быть до нескольких тысяч километров, а у станций предупреждения столкновений может иногда ограничиваться всего несколькими километрами.
Как структурный элемент дальность действия входит в более общую тактическую характеристику РЛС, зона обзора станции, определяющую область пространства, которую радиолокационная станция периодически осматривает и ведет в ней наблюдение за целями. Как видно из рисунка 3.1,  , по сути, определяет дальнюю границу зоны обзора.
, по сути, определяет дальнюю границу зоны обзора.
Рис. 3.1 Зона обзора РЛС
 и
и  - максимальный и минимальный угол места, под которыми РЛС может наблюдать за целями,
- максимальный и минимальный угол места, под которыми РЛС может наблюдать за целями,  - максимальная высота целей, за которыми РЛС может вести наблюдение,
- максимальная высота целей, за которыми РЛС может вести наблюдение,  - дальность действия РЛС.
- дальность действия РЛС.
Дальность  зависит от многих факторов. Во первых, она зависит от параметров самой радиолокационной станции, таких, как: мощность излучаемого сигнала, чувствительность приемника, коэффициента направленного действия антенны. Во вторых, она зависит от внешних факторов: эффективной площади рассеяния цели, затухания электромагнитных волн в атмосфере, помеховой обстановки и т.д. Поэтому для установления этих связей применяют так называемое основное уравнение радиолокации.
зависит от многих факторов. Во первых, она зависит от параметров самой радиолокационной станции, таких, как: мощность излучаемого сигнала, чувствительность приемника, коэффициента направленного действия антенны. Во вторых, она зависит от внешних факторов: эффективной площади рассеяния цели, затухания электромагнитных волн в атмосфере, помеховой обстановки и т.д. Поэтому для установления этих связей применяют так называемое основное уравнение радиолокации.
Уравнение, которое устанавливает связь дальности действия РЛС в свободном пространстве с техническими параметрами ее систем, характеристиками цели и внешними условиями, называется основным уравнением радиолокации.
Уравнение радиолокации используется при проектировании РЛС любого назначения, предъявления требований к основным трактам и системам РЛС, выборе оптимального режима работы в конкретной воздушно помеховой обстановке, оценке степени влияния условий и качества эксплуатации на боевые возможности РЛС.
Для того, чтобы установить основные зависимости, определяющие дальность радиолокационного наблюдения, рассмотрим простейший случай обнаружения цели в свободном пространстве. Анализ будем вести, предполагая, что атмосфера однородна и отсутствует затухание электромагнитных волн.
Пусть в некоторой точке пространства на расстоянии  от радиолокационной станции находится цель с эффективной площадью рассеяния
от радиолокационной станции находится цель с эффективной площадью рассеяния  (рис.3.2). Для упрощения будем считать, что передающая антенна РЛС является изотропной и равномерно излучает электромагнитную энергию во все области пространства, вследствие чего фронт волны будет представлять собой сферическую поверхность площадью
(рис.3.2). Для упрощения будем считать, что передающая антенна РЛС является изотропной и равномерно излучает электромагнитную энергию во все области пространства, вследствие чего фронт волны будет представлять собой сферическую поверхность площадью  .
.
На этом основании плотность потока мощности прямой электромагнитной волны у цели  равна
равна
 , (3.0)
, (3.0)
где  мощность излучаемых колебаний.
мощность излучаемых колебаний.
Цель, являясь также изотропным излучателем, равномерно по всем направлениям рассеивает всю падающую на нее мощность  (рис 3.3).
(рис 3.3).
Рис.3.2.
Плотность потока мощности отраженной волны в точке расположения приемной антенны РЛС  равна
равна
 . (3.0)
. (3.0)
Подставив в (3.2) значение  из (3.1), получим:
из (3.1), получим:
 . (3.3)
. (3.3)
Умножая величину  на эффективную площадь приемной антенны
на эффективную площадь приемной антенны  , находим мощность отраженного сигнала, поступающего на вход приемника:
, находим мощность отраженного сигнала, поступающего на вход приемника:
 . (3.4)
. (3.4)
Рис.3.3.
Поскольку реальная антенна РЛС обладает направленными свойствами, учтем это введением коэффициента направленного действия передающей антенны  , устанавливающим, во сколько раз больше антенна способна излучать электромагнитную энергию в заданном направлении по сравнению с изотропной антенной:
, устанавливающим, во сколько раз больше антенна способна излучать электромагнитную энергию в заданном направлении по сравнению с изотропной антенной:
 .
.
Из теории антенн известно, что между эффективной площадью приемной антенны  и ее коэффициентом усиления по мощности
и ее коэффициентом усиления по мощности  существует зависимость
существует зависимость
 , (3.5)
, (3.5)
справедливая для любого направления в зоне излучения и зоне приема рассматриваемой антенны. С учетом формулы, (3.5) мощность принимаемого сигнала
 (3.6)
(3.6)
Это выражение можно записать иначе, если учесть, что коэффициент направленного действия  и коэффициент усиления приемной антенны
и коэффициент усиления приемной антенны  связаны соотношением
связаны соотношением
 , (3.7)
, (3.7)
где  коэффициент полезного действия антенны. Как правило, для радиолокационных антенн
коэффициент полезного действия антенны. Как правило, для радиолокационных антенн  и можно полагать, что
и можно полагать, что  . Тогда мощность принимаемого сигнала
. Тогда мощность принимаемого сигнала
 (3.8)
(3.8)



















