МУ к выполнению ДЗ по КШО - Власов, Складчиков (1031222), страница 4

Просмтор этого файла доступен только зарегистрированным пользователям. Но у нас супер быстрая регистрация: достаточно только электронной почты!

Текст из файла (страница 4)

2.1. Расчёт основных параметров цилиндра гидравлического пресса

Гидравлические прессы широко применяются для ковки слитков, ковки и штамповки крупных поковок, прессования профилей из стали, алюминиевых и магниевых сплавов.

Наиболее нагруженной и ответственной деталью гидравлического пресса является его рабочий цилиндр, от работоспособности которого зависят эксплуатационные качества и надежность всего пресса.

При проектировании гидравлического пресса конструктор должен решить вопрос о давлении рабочей жидкости, так как давлениt определяет конструкцию всех основных узлов пресса и в первую очередь рабочего цилиндра. Чем крупнее пресс, тем важнее определение целесообразного давления рабочей жидкости. При рациональном выборе величины давления рабочей жидкости стоимость изготовления пресса и эксплуатационные затраты могут быть значительно снижены.

Цилиндры гидравлических прессов бывают с опорой на фланец и с опорой на дно. Наибольшее распространение получили цилиндры первого типа (рис. 2.1), которые состоят из трех основных частей: трубы цилиндра, опорного фланца и днища.

Домашнее задание предусматривает расчет цилиндра с опорой на фланец.

Основным параметром из всех, которые приходится учитывать при выборе давления рабочей жидкости, является наружный диаметр цилиндра в его средней части, так как он определяет габаритные размеры и массу наиболее тяжелой детали пресса – поперечины. Размеры фланца и днища не влияют на габариты поперечины. Поэтому за основу при выводе зависимостей, связывающих габариты цилиндра и давление рабочей жидкости, приняты формулы для расчета на прочность цилиндра в его средней части, удаленной от опорного фланца и днища на расстояние более 0,75 , где справедливы формулы Ламе. В этой части, называемой зоной Ламе, главные напряжения на внутренней, наиболее нагруженной поверх-

Рис. 2.1. Типы силовых цилиндров с опорой на фланец: а) плунжерный;

б) дифференциальный; в) поршневой

1– цилиндр; 2 – плунжер; 3 – направляющая втулка; 4 – уплотнение; 5 – нажимная

втулка; 6- нажимной фланец; 7 – грундбукса; 8 - поршень; 9- шток.

и -внутренний и наружный диаметры цилиндра;

- диаметр плунжера; – диаметр штока.

ности цилиндра (рис. 2.2), определяются по формулам Ламе:

(39)

где: р- давление рабочей жидкости; σ_{t ,} σ_z, σ_r – тангенциальное (окружное), осевое и радиальное напряжения; - внутренний и наружный радиусы цилиндра.

Эквивалентное напряжение по энергетической теории прочности на внутренней поверхности цилиндра в его средней части (в зоне Ламе)

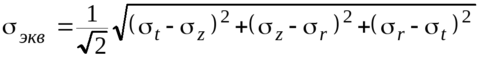. (40)

Подставив в выражение (40) напряжения по формулам Ламе (39), получим

. (41)

Приняв, что допускаемое напряжение , получим

; (42)

г

де σ_т – предел текучести, и n_т – коэффициент запаса по текучести материала цилиндра.

Значение n_т устанавливается с учетом концентрации напряжений в местах примыкания трубы цилиндра к фланцу и к днищу цилиндра и принимается равным 2,5…3..

Номинальная сила пресса с одним рабочим цилиндром:

; (43)

откуда

, (44)

где r_п – радиус плунжера (поршня) цилиндра.

Тогда

, (45)

где – коэффициент, учитывающий зазор между плунжером и внутренней поверхностью цилиндра; . Для поршневых цилиндров .

Из формулы (42) следует

. (46)

С учетом формул (42) – (46) получим

. (47)

Если в формулу (47) подставить постоянные значения P_н, [σ] и , то можно построить график D_н=f(p), имеющий экстремум –минимальное значение наружного диаметра цилиндра D _н.опт при оптимальном давлении рабочей жидкости p_опт (рис. 2.3).

В

зяв первую производную из уравнения (47) и приравняв ее нулю, получим

. (48)

Значение p_опт пропорционально значению допускаемого напряжения :

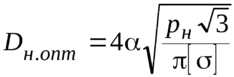. (49)

Разделив левые и правые части уравнений (47) и (49) друг на друга, получим:

. (50)

На рис. 2.4 изображен график зависимости, построенной по формуле (50), в координатах . Применение безразмерных относительных координат позволяет использовать этот график для расчёта любых цилиндров независимо от их габаритов, допускаемых напряжений и применяемого давления рабочей жидкости.

Начальный участок графика слева от точки оптимума характерен медленным увеличением ординаты при значительном уменьшении абсциссы. При =0,2…0,22 имеем =1.05…1,02. Т. е. уменьшение давлеления рабочей жидкости на 24…31% по сравнению с оптимальным приводит к увеличению наружного диаметра цилиндра всего лишь на 3…5% . Такое давление, меньшее оптимального, называется рациональным [6] и позволяет применять насосы пониженного давления с меньшими гидравлическими потерями, снижает требования к гидравлическим уплотнениям,- уменьшает работу сжатия жидкости в рабочем цилиндре. Кроме того, при рациональном давлении цилиндр легче, так как стенки трубы у него значительно тоньше.

Для реализации преимуществ рационального давления жидкости можно пользоваться таблицей 3 стандартных значений давления. Предпочтительно для каждого значения давления применять наибольшие рекомендуемые в табл. 3 значения допускаемого напряжения .

У цилиндров с опорой на дно на внутренней поверхности в зоне Ламе двухосное напряженное состояние (σ_z=0), и для таких цилиндров оптимальное давление

, (51)

Для цилиндров, опирающихся на фланец или на дно . В работе [7] рекомендуются следующие значения допускаемого напряжения [σ]: для стальных литых цилиндров [σ]=80…100 МПа; для кованых цилиндров из стали, содержащей 0,30…0,35% С, [σ]=110…150 МПа; для кованых цилиндров из малолегированной стали, содержащей 1,5…2,0 Ni , [σ]=150…180 МПа.

2.2. Прочностной расчёт опорного фланца цилиндра

Там, где трубная часть цилиндра переходит во фланец, в стенках цилиндра действуют внутренние силовые факторы (растягивающая сила Р, изгибающий момент М, перерезывающая сила Q, (рис. 2.5) и возникают дополнительные напря-

ж

ения, связанные с изгибом фланца от сил реакции опорной кольцевой поверхности поперечины. Прочность цилиндра вблизи фланца определяется напряженным состоянием на его наружной поверхности, где осевое напряжение σ_z в несколько раз превышает номинальное, рассчитанное по второй формуле Ламе (39).

Наиболее опасное двухосное напряженное состояние в галтели А перехода трубной части цилиндра во фланец (рис. 2.6), где главные напряжения в осевом и тангенциальном направлении можно определить по следующим формулам, полученным на основе методики, разработанной в проектной организации ВНИИМЕТМАШ [8]:

; 52)

; (53)

, (54)

где

,

,

,

μ

– коэффициент Пуассона, при расчетах принимается равным 0,3;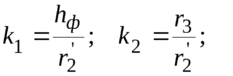 и – внутренний и наружный радиусы цилиндра там, где на внутренней поверхности цилиндра сделана расточка диаметром 2 для бронзовой направляющей втулки плунжера и для узла гидравлического уплотнения (см. рис. 2.1а). Наружный диаметр бронзовой втулки (диаметр расточки) назначается с учетом необходимой толщины стенки втулки для возможности ее изготовления. Если расточка отсутствует, то в формулах (52) – (54) . Напряжения σ_z и σ_t зависят от размеров фланца: наружного радиуса r₃ и высоты (толщины) фланца h_ф. В зоне перехода трубы цилиндра во фланец выполняют галтель радиусную, косыночную или эллиптическую. Для радиусной галтели r_ф=b(r₂-r₁), где b=0,20…0,25. Формулы (52) – (53) выведены для случая, когда отсутствует переходная галтель. Они не учитывают, что переходная галтель увеличивает стенку цилиндра и снижает концентрацию напряжений. Площадь кольцевой опорной поверхности фланца

, (55)

Среднее контактное напряжение на опорной поверхности фланца

. (56)

Решим уравнение (56) относительно r₃

. (57)

Формула (57) справедлива и для других типов галтели, так как их ширина в радиальном направлении так же равна величине r_ф (высота косыночной и эллиптической галтели больше r_ф ).

Необходимо учитывать неравномерность распределения контактных напряжений вследствие различной жесткости поперечины по окружности опорной поверхности фланца и отклонения равнодействующей силы деформирования заготовки (слитка) при эксцентричном нагружении пресса. Поэтому при определении напряжений по формулам (52) – (53) считают, что сила реакции поперечины на цилиндр Р₁ приложена к самой кромке фланца на расстоянии r₃ от его оси (см. рис. 2.6). Радиус фланца r₃ не следует увеличивать более расчетного значения, полученного по формуле (57), так как чем больше r₃, тем больше напряжения σ_z и σ_экв в галтели А. При расчетах также принимают, что среднее контактное напряжение должно быть не более 80 МПа.

Чем больше высота фланца h_ф, тем меньше растягивающее осевое напряжение σ_z и эквивалентное напряжение σ_экв в галтели А, но тем тяжелее цилиндр. Обычно при проектировании принимают

или , где с = 1,5…2,5.

По формулам (52), (53) и (54) выполняют поверочный расчет на прочность опорного фланца при наименьшем значении , например, когда коэффициент с=1,5. Сравнивают полученный результат эквивалентного напряжения σ_экв с принятым ранее допустимым напряжением [σ] и пределом текучести материала цилиндра σ_т . Необходимо выполнить несколько вариантов расчета по формулам (52) – (54) при различных значениях относительной высоты фланца . Высота фланца h_ф зависит от выбора величины коэффициента с. Можно принять с=1,5; 2,0; 2,5. Это позволит быстро определить наиболее приемлемое значение h_ф.

Характеристики

Список файлов книги