Курс лекций (1027826), страница 3

Просмтор этого файла доступен только зарегистрированным пользователям. Но у нас супер быстрая регистрация: достаточно только электронной почты!

Текст из файла (страница 3)

Вероятность нахождения системы в состоянии P_ij может быть вычислена как вероятность P_ij, умноженная на вероятность П_ij:

1. P_ij = P_i * П_j → (2)

P_ij – вероятность того, что в системе i заявок 1-ого типа независимо от того, сколько заявок 2-ого типа.

Объединение для 1-ого типа заявок можно сделать совершенно точно.

0 = - P₀₀*λ₁ + P₁₀*μ₁ + P₀₁*μ₂ - P₀*λ₂

0 = - P₀₁*λ₁ + P₀₀*λ₂ - P₀₁*μ₂ + P₀₃*μ₂ - P₀₁*λ₂ + P₁₁*μ₁

0 = - P₀₂*λ₁ + P₀₁*λ₂ - P₀₂*μ₂ + P₀₃*μ₂ - P₀₂*λ₂ + P₁₂*μ₁

- P₀₀*λ₁ - P₀₁*λ₁

Если мы объединим все вертикальные состояния:

Для первого варианта можно получить значения P:

(3) P₀ = 1 – ρ

P₁ = P₀*ρ

P₂ = P₀*ρ²

……..

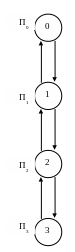
П₀

П₁ = P₀₁ + P₁₁ + P₂₁

Переход из П₁ в П₀ -

П₁

П₀

П₂

ЛЕКЦИЯ №8.

Пример использования метода свертывания по гиперплоскостям.

Два обслуживающих аппарата, но обслуживание ограничено, так как могут быть очереди.

Система: ξ { ξ₁ (t), ξ₂ (t)}

Возможны два случая:

1. взаимопомощь (если имеется в системе какое-то количество заявок, но меньше, чем количество обслуживающих аппаратов, то свободные обслуживающие аппараты могут оказывать помощь другим обслуживающим аппаратам, и, тем самым, несколько повышается интенсивность обработки обслуживания).

2. Если есть дисциплина обслуживания, то вводится коэффициент взаимопомощи.

μ₁ – обслуживание заявок первого приоритета;

μ₂ – обслуживание заявок вторового приоритета.

P₁

P₀

P₂

P₃

P₄

μ_э1 = μ₂* P₀ + μ₂* P₁ = μ₂*( P₀ + P₁)

μ_э2 = 2μ₂* P₀ + μ₂* P₁

μ_э3 = 2μ₂* P₀ + μ₂* P₁

……….

P_ij = P_i* П_j

μ_э32 = 2μ₃* П₀ + μ₃* П₁

Показатели надежности объектов, восстанавливаемых вне процесса применения.

Эксплуатация проводится отдельно, ремонт – отдельно.

Считаем, что будет мгновенное восстановление.

Т₁ = T¹ + T² +… Tⁿ – суммарная наработка на отказ до n-ого отказа

Рассмотрим поток случайных событий (отказов) – проявлений отказаов в какой-то случайный момент времени.

Поток отказов может характеризоваться ведущей функцией (математическое ожидание числа отказов на интервале (0;t), которое характеризует среднее число отказов, ожидаемых в малом интервале наработки, определяемый для рассматриваемого момента t суммарной наработки – Ω (t)).

В ТМО при изучении потоков событий используют две основные характеристики:

- интенсивность потока событий:

- параметр потока событий

(k – количество событий за интервал времени; P_k – вероятность того, что произойдет k событий за ).

Если потоки ординарные, то есть вероятность появления более одного события бесконечно мала, то мы можем считать, что:

Из этого следует, что интенсивность и параметр потока – одинаковые величины. Не путать с параметром потока отказов восстанавливаемых системинтенсивность потока отказов невосстанавливаемых систем.

Всегда рассматриваем ординарный поток:

Вероятность того, что

В очень редких случаях допускать отсутствие последействия нельзя. В качестве изделий реальных процессов можно рассматривать потоки с ограниченным последействием, в которых значение наработки между последовательными отказами являются случайными независимыми последействиями.

Ограничение последействия → вероятность появления отказа за наработку (t₁;t₂) зависит от наработки, накопленной от последнего отказа, и не зависит от того, когда происходят предыдущие отказы.

Если случайные величины наработки одинаково распределены и независимы, то параметр потока отказов, связанный с плотностью распределения наработки между отказами следующим соотношением:

Уравнение Вальтера второго рода с разностным ядром. Это уравнение не всегда решается в явном виде.

Тогда:

(если не зависит)

Пример:

В ТЗ задается:

t_p – срок эксплуатации

При

- среднее время наработки на отказ восстанавливаемого объекта.

ЛЕКЦИЯ №9.

Параметры потока отказов могут меняться в худшую сторону.

Чтобы этого избежать этого, надо проводить соответствующие мероприятия, то есть проводить профилактические и регламентационные работы для того, чтобы снизить параметр потока отказов. Считается, что система как бы обновляется. Мы выискиваем скрытый отказ в системе и устраняем его.

Показатели надежности восстанавливаемых систем в процессе применения.

1. системы, которые допускают какие-то перерывы в своей работе.

2. системы, которые не допускают перерывов в своей работе.

Предусматривается почти обязательно избыточность аппаратуры → переход на резервное, или реконфигурация системы. Для такого рода систем чрезвычайно важное значение имеет свойство готовности (способность находиться в процессе эксплуатации значительную долю времени в работоспособном и готовом к применению состоянии).

t_P1, t_В2 – случайные величины

T_i = t_Pi + t_Вi

Композиция случайных величин:

f(x) – плотность распределения времени безотказаной работы;

g(t) – плотность распределения времени восстановления объектов.

- плотность распределения n-го восстановления.

Другой показатель – вероятность застать систему в работоспособном состоянии – Г(t).

Функция готовности:

Г(t) + П(t) = 1

(П (t) – функция неготовности)

Объект может находиться в момент t в работоспособном состоянии при осуществлении одного из двух несовместных событий:

1. объект в течении времени (0;t) не отказал

2. объект отказал и восстанавливается, и после последнего отказа (к моменту времени t) объект больше не отказывал.

Функция готовности Г(t) равна сумме вероятностей указанных событий.

Вероятность первого события:

малый интервал времени: (τ;τ-dτ) – этому малому интервалу предшествует время работы.

Тогда вероятность того, что на этом малом интервале закончится n-ое восстановление, и объект больше не откажет за оставшийся промежуток времени t-τ и равно:

f₀ * τ(τ)dτ*P(t- τ) = dτ* P(t- τ)

t₀ – параметр потока восстановления

F (t) = P(t) +

F (t) – функция готовности

Согласно узловой теореме теории восстановления:

где - математическое ожидание времени между очередными событиями

- возрастающая функция на

- математическое ожидание числа отказов на интервале

Математическое ожидание T₀ = T_P + T_В

Тогда функция готовности будет иметь вид:

Но этот коэффициент недостаточен для характеристики всей системы, так как эта величина относительная.

В подавляющем большинстве случаев К_г недостаточен. Нужны еще дополнительные характеристики (которые могут дать реальные интервалы действия и времени).

Таким образом, функция готовности в пределе при переходит коэффициент готовности.

Коэффициент готовности определяется как вероятность того, что объект окажется в работоспособном состоянии в произвольный момент времени, кроме планируемых периодов, в течении которых применение объекта не предусмотрено.

Коэффициент готовности можно понимать как долю времени, в течении которого объект способен работать.

При фиксированном значении М(t) стационарный режим наступает тем медленнее, чем меньше дисперсия случайной величины T₀. Очень часто используется коэффициент готовности за период эксплуатации:

( - время службы)

Если , то

Если считать, что функция распределения экспоненциальная, то тогда:

t ; t+τ

Функция готовности Г_уст (устанвившаяся):

- коэффициент оперативной готовности

При допущении экспоненциальности законов распределения процесс изменения состояния объекта будет марковским с непрерывным временем и конечным множеством состояний. Определим вероятность того, что объект окажется работоспособным в момент времени (t;t+Δt). Обозначим нахождение объекта в работоспособном состоянии в момент времени t как P(t) (не путать с P(t) – вероятность безотказной работы на интервале ).

Объект может находиться в работоспособном состоянии при следующих событиях:

1. работоспособный объект к моменту времени t останется работоспособным в течение времени Δt.

2. Неработоспособный объект к моменту t будет за время Δt восстановлен.

P₀(t)*(1-λΔt)

Вероятность того, что к моменту (t;t+Δt) объект будет в рабочем состоянии.

ЛЕКЦИЯ №10.

Интенсивность отказа - по экспоненте.

Если =const, =const в начальный момент (переходной период), то функция готовности может быть приравнена к вероятности безотказной работы на интервале (0, t).

.

Чтобы избежать трудоемкости вычисления функции готовности можно приблизительно считать, что до некоторого времени t₁ функция готовности принимаем как функцию времени безотказной работы.

При

Чем выше загрузка, тем резче уходит вниз.

Системы, не допускающие сбоев работы, должны содержать избыточность (аппаратную, информационную). Для повышения надежности таких систем с позиции аппаратуры вводится резервирование элемента (или системы в целом), что приводит к значительному повышению коэффициента готовности:

Считаем, что переключатель идеальный.

Характеристики

Список файлов лекций