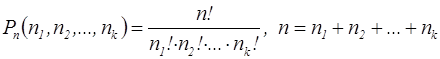Комбинаторика
2020-06-032021-03-09zzyxelСтудИзба
Глава 12. Комбинаторика.
Сколькими способами можно выбрать n элементов из k?
§1. Размещения.
- число размещений из n элементов по k
§2. Перестановки.
- число перестановок из n элементов. 0! = 1.
§3. Сочетания.
- число сочетаний из n элементов по k
Рекомендуемые материалы
25 ВАРИАНТ полное домашнее задание (Кон. автомат + комбинаторика ИУ7)
РК № 2 Практика ( 12 Билетов )
Необходимо найти максимальное значение целевой функции F = 2x1+3x2 → max, при системе ограничений: 3x1+x2≤12, (1) x1+3x2≤12, (2) x1+2x2≥3, (3) 2x1+x2≥3, (4) x1 ≥ 0, (5) x2 ≥ 0, (6)
FREE
Вопросы ко второму модулю для СМ1, СМ2, СМ3, СМ4, СМ6, СМ8, СМ9, СМ10, СМ12, РК4 (с сайта кафедры ФН-4)
Задачи 1 и 2. Комбинаторика. 19 вариант
FREE
вопросы для подготовки к 3-му модулю для СМ1, СМ2, СМ3, СМ4, СМ6, СМ8, СМ9, СМ10, СМ12, РК4 (с сайта кафедры ФН-4)
Порядок выбора элементов не важен
- рекуррентное соотношение. Треугольник Паскаля.
бином (Ньютона)
Биномиальные коэффициенты
§4. Размещения и сочетания с повторениями.
Люди также интересуются этой лекцией: 13.4 Особенности функционирования ускорителя трехмерной графики.
- число размещений с повторениями из n элементов по k
- число сочетаний с повторениями из n элементов по k
§5. Перестановки с повторениями.
![](https://s.studizba.com/z.php?f=/templates/si/i/noavatar.png&w=100&h=100&t=1"){kind=avatar}
