Формула Стокса
Лекция 9 Формула Стокса.
Ротор векторного поля.
Назовем ротором векторного поля  вектор
вектор
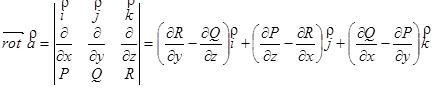
Свойства ротора.
Рекомендуемые материалы
1) Линейность 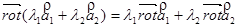
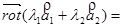
 =
=  +
+
 =
=  .
.
2)  - постоянное векторное поле.
- постоянное векторное поле.
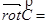
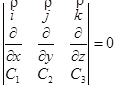
3) 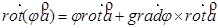
 =
=
 +
+ =
=  .
.
Теорема Стокса.
Пусть пространственно односвязная область V содержит кусочно-гладкую поверхность  с кусочно-гладкой границей
с кусочно-гладкой границей  .
.
Пусть компоненты векторного поля  непрерывны и имеют непрерывные частные производные по своим аргументам до второго порядка включительно в области V.
непрерывны и имеют непрерывные частные производные по своим аргументам до второго порядка включительно в области V.
Тогда справедлива формула Стокса
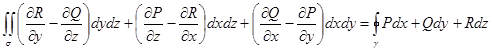
Замечание. Нормаль к поверхности  проведена так, чтобы наблюдатель, находясь на конце вектора нормали, видел бы обход контура
проведена так, чтобы наблюдатель, находясь на конце вектора нормали, видел бы обход контура  , совершающимся в положительном направлении (так, чтобы область, границей которой является контур, при обходе контура находилась бы «по левую руку»).
, совершающимся в положительном направлении (так, чтобы область, границей которой является контур, при обходе контура находилась бы «по левую руку»).
Доказательство теоремы Стокса.
|
| Как и формула Остроградского – Гаусса, формула Стокса состоит из трех независимых частей (в силу произвольности компонент векторного поля). Докажем одну из этих частей, остальные формулы доказываются аналогично. Докажем Предположим, что поверхность |
представляет собой вектор 
Отсюда видно, что  . Вспомним еще, что
. Вспомним еще, что  .
.
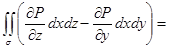
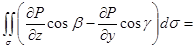
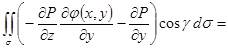
(на поверхности 
 , поэтому под интегралом стоит частная производная P по y с учетом зависимости z от y на поверхности
, поэтому под интегралом стоит частная производная P по y с учетом зависимости z от y на поверхности )
)
= 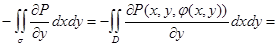
Используем формулу Грина для области D с ее границей  . Ее можно записать в виде
. Ее можно записать в виде
 . Нам понадобится только та ее часть, которая относится к функции P
. Нам понадобится только та ее часть, которая относится к функции P  . Продолжаем равенство дальше.
. Продолжаем равенство дальше.
= .
.
В самом деле, на контуре  , а переменные x, y на том и другом контуре те же, так как контур
, а переменные x, y на том и другом контуре те же, так как контур  - это проекция контура
- это проекция контура  на плоскость OXY (параллельно оси OZ).
на плоскость OXY (параллельно оси OZ).
Одна из частей формулы Стокса доказана.
Линейным интегралом векторного поля  по дуге L называется криволинейный интеграл
по дуге L называется криволинейный интеграл  .
.
Линейный интеграл имеет смысл работы векторного поля при перемещении по дуге.
Циркуляцией векторного поля называется линейный интеграл по замкнутому контуру.
 .
.
Вводя эти понятия, можно записать формулу Стокса в «полевой» форме
 .
.
Мы определили ротор векторного поля в декартовой системе координат, однако ротор – это характеристика самого векторного поля Поэтому необходимо дать определение ротора, которое не зависит от выбора системы координат.
Инвариантное определение ротора.
Рассмотрим произвольную точку M в области V. Проведем через нее поверхность  , границей которой служит контур
, границей которой служит контур  . Пусть поверхность и контур удовлетворяют условиям теоремы Стокса. По теореме о среднем для поверхностного интеграла и формуле Стокса получим
. Пусть поверхность и контур удовлетворяют условиям теоремы Стокса. По теореме о среднем для поверхностного интеграла и формуле Стокса получим
 .
.
Здесь, как и ранее  - обозначение области и ее площади. Из этого соотношения, стягивая контур
- обозначение области и ее площади. Из этого соотношения, стягивая контур  к точке M, получим
к точке M, получим
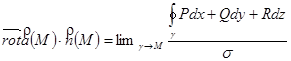
Это и есть инвариантное определение ротора.
Правая часть формулы – это поверхностная плотность циркуляции векторного поля (энергии в точке M вращения векторного поля или работы векторного поля при вращении вокруг некоторого направления, определяемого вектором  ). Левая часть – это проекция ротора на это направление.
). Левая часть – это проекция ротора на это направление.
Если направление  совпадает с направлением ротора и
совпадает с направлением ротора и  - единичный вектор, то левая часть равна модулю ротора. Поэтому модуль ротора векторного поля равен максимальному значению поверхностной плотности циркуляции векторного поля.
- единичный вектор, то левая часть равна модулю ротора. Поэтому модуль ротора векторного поля равен максимальному значению поверхностной плотности циркуляции векторного поля.
Левая часть достигает максимума при коллинеарности направления и ротора векторного поля. Поэтому направление ротора векторного поля – это то направление, вокруг которого поверхностная плотность циркуляции векторного поля – наибольшая.
Пример. Найти ротор линейной скорости вращения с постоянной угловой скоростью 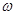
Векторное поле линейной скорости  .
.
 ,
,
Ранее была сформулирована теорема о полном дифференциале для пространственной кривой. В ее доказательстве не хватало только одного пункта – перехода от пункта 3) к пункту 2). Все остальное доказывается аналогично случаю плоской кривой.
Теорема (о полном дифференциале) для пространственной кривой.
Пусть дуга AB лежит на кусочно-гладкой поверхности S, пусть функции P(x, y, z), Q(x, y, z), R(x, y, z) непрерывны и имеют непрерывные частные производные на S. Тогда следующие четыре утверждения эквивалентны.
1)  не зависит от формы дуги (от пути интегрирования), а зависит только от начальной и конечной точек дуги.
не зависит от формы дуги (от пути интегрирования), а зависит только от начальной и конечной точек дуги.
2) Для любого замкнутого контура 
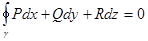
3) 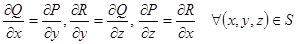
4)  .
.  - полный дифференциал.
- полный дифференциал.
Теперь переход от пункта 3) к пункту 2) легко сделать по формуле Стокса.
Криволинейный интеграл от полного дифференциала можно вычислять по формуле
 =
=  , так как интеграл не зависит от формы дуги (пути интегрирования).
, так как интеграл не зависит от формы дуги (пути интегрирования).
Криволинейный интеграл от полного дифференциала можно вычислять также по формуле Ньютона – Лейбница
 =
=  , где
, где  - потенциал векторного поля (
- потенциал векторного поля ( ).
).
Потенциальное поле и его свойства.
Векторное поле 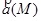 называется потенциальным, если существует такое скалярное поле
называется потенциальным, если существует такое скалярное поле  (потенциал векторного поля
(потенциал векторного поля 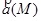 ), что
), что 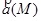 =
= .
.
Замечание. Если поле 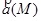 - потенциально, то
- потенциально, то 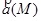
 =
=  - полный дифференциал. Тогда
- полный дифференциал. Тогда  - полный дифференциал. Поэтому свойства потенциального поля можно сформулировать и доказать как следствия теоремы о полном дифференциале.
- полный дифференциал. Поэтому свойства потенциального поля можно сформулировать и доказать как следствия теоремы о полном дифференциале.
Свойства потенциального поля.
1. Линейный интеграл потенциального поля  не зависит от формы дуги L =
не зависит от формы дуги L =  , а зависит только от начальной и конечной точек дуги.
, а зависит только от начальной и конечной точек дуги.
В самом деле,  =
= .
.
2. Циркуляция потенциального поля равна нулю
Полагая дугу АВ замкнутой (A = B), получаем  =
= 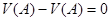
3. Потенциальное поле является безвихревым, т.е. 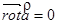
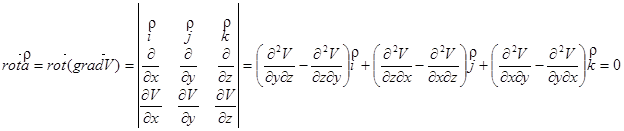
Оператор Гамильтона
Оператор Гамильтона  .
.
Применим оператор Гамильтона к скалярному полю  .
.
Оператор Гамильтона представляет собой вектор-оператор. Его можно скалярно или векторно умножить на векторное поле  .
.
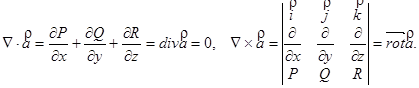
Это дифференциальные операции первого порядка над скалярным и векторным полями. От скалярного поля можно взять градиент, от векторного поля можно взять дивергенцию и ротор.
Дифференциальные операции второго порядка.
В результате дифференциальных операций первого порядка мы получаем скалярные и векторные поля  .
.
К ним вновь можно применить дифференциальные операции первого порядка.
От скалярного поля  можно взять градиент, получив векторное поле
можно взять градиент, получив векторное поле  .
.
От векторных полей  можно взять ротор и дивергенцию, получив скалярные поля
можно взять ротор и дивергенцию, получив скалярные поля  ,
,  и векторные поля
и векторные поля  ,
,  .
.
Итак, дифференциальные операции второго порядка позволяют получить скалярные поля  ,
,  и векторные поля
и векторные поля  ,
,  ,
,  .
.
Ранее было показано, что потенциальное поле – безвихревое, т.е.  =0.
=0.
Покажем, что поле ротора – соленоидальное поле, т.е.  =0.
=0.
Доказательство.
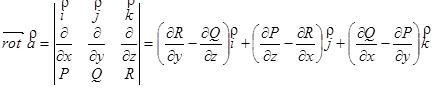
 =
=  .
.
Три остальных векторных поля связаны друг с другом. Это становится ясным, если рассматривать векторные операции с оператором Гамильтона «набла» аналогично обычным векторным операциям. Однако, эти аналогии не совсем верны, см. подробнее о свойствах оператора «набла» выпуск 7 учебника.
 =
= ,
, 
 =
= 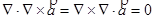
Известно соотношение  . Перенося это правила на действия с оператором «набла», получим
. Перенося это правила на действия с оператором «набла», получим
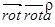
 .
.
Здесь  - оператор Лапласа (скаляр – оператор).
- оператор Лапласа (скаляр – оператор).
 .
.
 - произведение скаляр-оператора Лапласа на вектор
- произведение скаляр-оператора Лапласа на вектор  .
.
Гармоническое поле.
Скалярное поле  называется гармоническим, если
называется гармоническим, если
Бесплатная лекция: "14.4 Революция 1905-1907 гг" также доступна.
 - уравнение Лапласа.
- уравнение Лапласа.
Векторное поле называется гармоническим, если оно потенциальное ( ), а потенциал
), а потенциал  - гармоническое скалярное поле, т.е.
- гармоническое скалярное поле, т.е.  .
.
Теорема. Для того, чтобы векторное поле 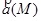 было гармоническим, необходимо и достаточно чтобы оно было соленоидальным и потенциальным.
было гармоническим, необходимо и достаточно чтобы оно было соленоидальным и потенциальным.
Необходимость. Если векторное поле 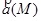 - гармоническое, то оно потенциальное, т.е.
- гармоническое, то оно потенциальное, т.е.  , тогда оно соленоидально, так как
, тогда оно соленоидально, так как  .
.
Достаточность. Если векторное поле 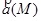 потенциальное, то
потенциальное, то  . Так как оно еще и соленоидально, то 0 =
. Так как оно еще и соленоидально, то 0 =  . Следовательно, поле потенциально и его потенциал удовлетворяет уравнению Лапласа, поэтому векторное поле – гармоническое.
. Следовательно, поле потенциально и его потенциал удовлетворяет уравнению Лапласа, поэтому векторное поле – гармоническое.
Так как гармоническое поле потенциально и соленоидально, то его свойства – свойства соленоидального поля и свойства потенциального поля.



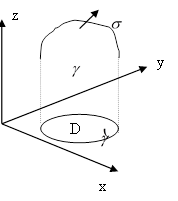

 - часть формулы Стокса, в которой содержится только компонента P.
- часть формулы Стокса, в которой содержится только компонента P. 


















