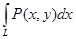Формула Грина

Лекция 6. Формула Грина.

Теорема (формула) Грина. Пусть G – плоская односвязная область с кусочно-гладкой границей L. Пусть функции P(x, y), Q(x, y) непрерывны и имеют непрерывные частные производные по своим переменным в области G и на L.

Тогда справедлива формула Грина

.

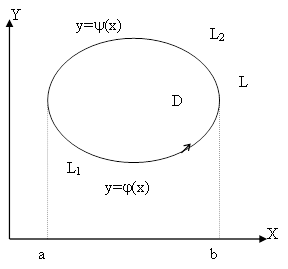
Доказательство. 1) Назовем плоскую область D (в плоскости OXY) правильной, если любая прямая, параллельная координатной оси (OX или OY) пересекает область не более, чем в двух точках. Можно показать, что область G можно представить как объединение конечного числа правильных областей .

 Тогда по свойству аддитивности двойной интеграл в правой части формулы Грина равен сумме двойных интегралов по правильным областям.  Криволинейный интеграл в левой части равен сумме криволинейных интегралов по границам правильных областей, так как криволинейные интегралы по общим границам любых правильных областей различны по знаку из-за различных направлений обхода границы и взаимно уничтожаются при суммировании.

Поэтому доказательство может быть проведено для правильной области G.

2) Пусть G – правильная область. Так как P, Q могут быть произвольными функциями, то формула Грина сводится двум формулам  и , каждую из которых надо доказать. Докажем первую формулу, вторая доказывается аналогично.

Вычисление площади области по формуле Грина.

По свойству 3 двойного интеграла площадь области D можно вычислить по формуле

. Поэтому достаточно выбрать P, Q так, чтобы , чтобы с помощью криволинейного интеграла по формуле Грина можно было бы вычислять площадь области.

Например, можно выбрать Q=x, P=0. Тогда  . Можно выбрать Q=0, P=y, тогда . Очень полезна бывает симметричная формула при .

Пример. Вычислить площадь эллипса с полуосями a, b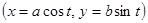

.

Полный дифференциал и его вычисление.

Теорема (о полном дифференциале). Для того чтобы выражение  - было полным дифференциалом некоторой функции - потенциала, необходимо и достаточно, чтобы в условиях формулы Грина было выполнено одно из следующих четырех условий (эквивалентных условий полного дифференциала)

1)  зависит только от начальной A и конечной B точек дуги  и не зависит от формы дуги (не зависит от пути интегрирования),

2)  для любого кусочно-гладкого контура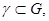

3) ,

4) .

Доказательство. Схема доказательства теоремы . По этой цепочке можно последовательно добраться от любого пункта к любому другому.

 Дополнительно предположим, что существуют и непрерывны вторые смешанные производные функции V. Тогда они равны.

.

. Это следует из формулы Грина.

. Пусть точки A, B соединены двумя дугами L₁ и L₂. Тогда из них можно составить контур , интеграл вдоль которого по п.2 равен нулю.

== -

. Поэтому =.

. Докажем, что  - потенциал, то есть, что

. Докажем первое соотношение, второе доказывается аналогично.

=

Заметим, что такая запись интеграла показывает, что интеграл не зависит от формы дуги. Поэтому мы можем в первом интеграле провести дугу через точку (x, y), чтобы  в первом и втором интеграле сократились интегралы по  дуге, соединяющей начальную точку с точкой  (x, y). В первом интеграле выберем в качестве дуги, соединяющей точку (x, y) с точкой (x+Dx) отрезок прямой, параллельный оси OX. На этом отрезке y не изменяется, поэтому dy=0

Тогда, продолжая равенство, получим

= =

(здесь мы перешли от криволинейного интеграла к определенному, так как дуга интегрирования – отрезок, параллельный оси OX и применили теорему о среднем для определенного интеграла). Теперь используем непрерывность функции P(x, y) по переменной x.

= . Первое соотношение доказано.

 Для доказательства второго соотношения варьируется переменная y, дуга, соединяющая точки (x_0, y₀), и (x, y+Dy) проводится  через точку (x, y)  и далее по отрезку, параллельному оси OY, соединяющему точки (x, y) и (x, y+Dy).

Формула Ньютона – Лейбница.

Пусть выполнены условия теоремы о полном дифференциале и пусть выражение

 - полный дифференциал, а функция - потенциал.

Тогда справедлива формула Ньютона – Лейбница

, где  - потенциал.

Доказательство. В теореме о полном дифференциале доказано, что потенциал можно записать в виде .   Так как интеграл не зависит от пути интегрирования, то дугу, соединяющую точки (x₁, y₁), (x₂, y₂) можно провести через точку (x₀, y₀). Поэтому = +  = -  = .

Теорема (о полном дифференциале) для пространственной кривой.

Пусть дуга AB лежит на кусочно-гладкой поверхности S, пусть функции P(x, y, z), Q(x, y, z), R(x, y, z) непрерывны и имеют непрерывные частные производные на S. Тогда следующие четыре утверждения эквивалентны.

1) не зависит от формы дуги (от пути интегрирования), а зависит только от начальной и конечной точек дуги.

2) Для любого замкнутого контура  

3)

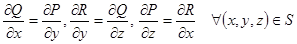
4) .   - полный дифференциал.

Доказательство. Доказательство аналогично двумерному случаю, схема доказательства та же: . Докажите ее самостоятельно.

 проводится по теореме о смешанных производных так же как в двумерном случае.

 проводится по теореме Стокса (будет сформулирована и доказана ниже).

 доказательство полностью аналогично двумерному случаю.

 доказательство аналогично двумерному случаю.

Замечание. Формула Ньютона-Лейбница справедлива в трехмерном случае и доказывается так же.

Вычисление криволинейного интеграла от полного дифференциала.

Криволинейный интеграл от полного дифференциала можно вычислять двумя способами.

1) Можно выбирать удобный путь интегрирования, например, состоящий из отрезков, параллельных OX и OY. На отрезке, параллельном OX, dy=0, так как y не изменяется на этом отрезке. На отрезке, параллельном OY, dx=0, так как x не изменяется на этом отрезке. Тогда = +

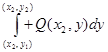
2) Можно восстановить потенциал, как это делалось на первом курсе при решении дифференциальных уравнений в полных дифференциалах и применить формулу Ньютона-Лейбница.

Пример. Вычислить интеграл .

1) =

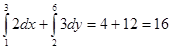
2)

.

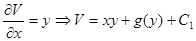
Сравнивая две записи потенциала, получим .

=.

Заметим, что аналогично вычисляется криволинейный интеграл от полного дифференциала по пространственной кривой.

Формула Грина для многосвязной области.

Пусть кусочно-гладкие контуры  лежат внутри контура и вне друг друга. Пусть  непрерывны и имеют непрерывные частные производные по переменным x, y в области между контурами и на самих этих контурах. Тогда  

=

=

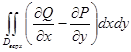
Складывая интегралы, получим

Рекомендация для Вас - 5. Частотные характеристики систем.

=.

Отсюда имеем

= . Теорема доказана для случая n = 2. Для n > 2 доказательство аналогично.

Следствие 1. Пусть Pdx+Qdy – полный дифференциал и n=1.

Тогда. Поэтому, если в какой-либо точке нарушается непрерывность функций, P, Q или их частных производных, то интеграл может быть взят по любому кусочно-гладкому не самопересекающемуся контуру, охватывающему эту точку (мы получим один и тот же результат).

Следствие 2. Пусть Pdx+Qdy – полный дифференциал Если кусочно-гладкий контур  один раз охватывает некоторую точку, , а контур L n раз охватывает эту точку, то в условиях теоремы . Докажите это самостоятельно.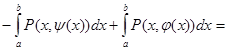