Задача линейного программирования и множители лагранжа

Задача линейного программирования и множители Лагранжа

Множители Лагранжа можно рассматривать для ЗЛП только в канонической форме записи.

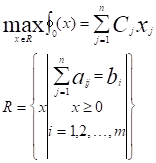
тогда можно построить функцию Лагранжа

Для оптимального решения

=

Таким образом двойственные переменные - суть множителя Лагранжа. Тогда функция Лагранжа для двойственной задачи запишется:

Рекомендуемые материалы

         Рассмотрим задачу линейного программирования в канонической форме записи:

 (1)

(2)-(3)

Составим функцию Лагранжа:

. (4)

Теорема. Задача линейного программирования (1)-(3) имеет решение тогда и только тогда, когда  такие, что функция Лагранжа достигает мавксимума в точке  в области .

Доказательство.

1. Необходимость. Пусть - оптимальное решение задачи(1)-(3).Покажем, что в точке  функция Лагранжа (4) достигает максимума в области .

Для доказательства построим двойственную задачу к данной:

 (5)

 (6)-(7)

         Т. к. задача (1)-(3) имеет оптимальное решение, то и задача (5)-(7) имеет оптимальное решение .

         Тогда будем иметь:

 (8)

По теореме двойственности . (9)

Откуда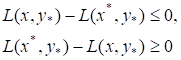

Или  при , значит, - точка максимума для функции Лагранжа (4).

2. Достаточность. . Требуется доказать, что - оптимальное решение задачи (5)-(7).

Предположим противное.

         Пусть существует , для которого (6) не выполняется:

,

.

Тогда функция Лагранжа перепишется в виде:

.

, т. е. .

Следовательно,  не является оптимальным решением, что противоречит условию. Тем самым мы показали, что - допустимое решение задачи (5)-(7), и выполняется условие (6):

. (10)

         Покажем, что для  выполняется соотношение (9). Предположим противное:

. (11)

Пусть существует индекс  такой, что  (12) (не выполняется (11)).

.

.

, что противоречит условию.

 Т. е. предположение, что существует индекс неверно. Следовательно, - оптимальное решение, для него верно (10), и это вытекает из теоремы двойственности.

Примечание.  (14)

Точка  называется седловой точкой.

Выпуклое программирование

         Рассмотрим задачу:

 (1)

 (2)

Функции - выпуклые функции.

         Задача (1)-(2) не имеет смысла, если область  не ограничена снизу. Во всех остальных случаях она имеет решение.

Теорема 1. Если  является аргументом локального минимума:

,

то  или .

Доказательство.

         Предположим противное. Пусть в области  существует , в котором .  Рассмотрим линейную комбинацию

.

Из определения выпуклости функции следует:

 (3)

Выражение (3) является условием выпуклости. Выберем  достаточно малым:

.

Т. о. получили две точки минимума, что противоречит свойству выпуклости функции . Следовательно, предположение о существовании точки  было неверным. Поэтому - точка глобального минимума функции .

Теорема Куна-Таккера.

 (1)

, (2)

где - выпуклые функции.

Условие Слейтера( необходимо для выполнения теоремы).

Теорема. будет решением задачи (1)-(2)когда существует вектор  и  такой, что вектор  является седловой точкой функции Лагранжа для задачи (1)-(2).

         Выясним, можно ли с помощью формализма Лагранжа решить линейную задачу.

.

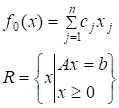
         Тогда получим ограничение для двойственной задачи

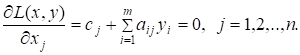
и для прямой задачи

Доказательство.

Пусть существует  и .

 (4)

Заметим, что (4) является условием седловой точки.

 (4’)

1. Требуется доказать, что  - точка минимума для задачи (1)-(2). Покажем, что  является дополнительным решением для задаи (1)-(2), т. е. что .

         Предположим противное. Пусть существует индекс , для которого условие (2) не выполняется, т. е. .

.

Задавая  достаточно большим, получим, что последнее выражение будет неограниченно возрастать, что противоречит условию (4’). Следовательно, предположение о том, что существует индекс , для которого не выполняется условие (2) было неверно. Таким образом, .

Теперь докажем, что  - точка минимума функции :

.

Рассмотрим правое неравенство из (4’):

.

Тогда , что и требовалось доказать.    

2. Необходимо построить множитель Лагранжа, чтобы имела место седловая точка. Причем, дано, что

.

         Рассмотрим два множества:

,

где  - выпуклые функции.

Тогда из построения следует, что  и  тоже являются выпуклыми множествами.

         Существует теорема о том, что два любых множества можно разделить гиперплоскостью, при условии, что эти множества не пересекаются. Пусть  - уравнение гиперплоскости.

         Т. к. точка  множества  не ограничена, то выберем ее таким образом, чтобы . Рассмотрим выражение:

.

Откуда следует, что .

.

Т. к. , то

.

По построению .

.

.

Это выражение является условием седловой точки.

         Точка  определяет минимум по  и максимум по .

.

Замечание. Практическое применение метода Лагранжа состоит в реализации следующего алгоритма:

,

.

1. Находим точку .

В лекции "Психология боевой деятельности" также много полезной информации.

2. , иначе см. пункт 4.

3. , пункт 5, иначе см. пункт 6.

4. , пункт 3.

5. , пункт 3.

6. .

Конец.