Описание решения оптимизационных задач линейных моделей с помощью табличного процессора еxcel
Описание решения оптимизационных задач линейных моделей с помощью табличного процессора Excel
Пример 11. Рассмотрим разобранную выше задачу №4:
Для изготовления четырех видов продукции (П1, П2, П3, П4) предприятие использует три типа ресурсов Р1, Р2, Р3. Размеры допустимых затрат ресурсов ограничены соответственно величинами 180, 210, 800. Нормы расхода ресурсов каждого типа на единицу продукции, их наличие в распоряжении предприятия, а также цена единицы продукции приведены в таб. 25.
Определить, сколько продукции каждого вида следует производить, если цель предприятия состоит в максимизации прибыли (сбыт продукции обеспечен).
Таблица 25
| Тип ресурса | Нормы расхода ресурсов на единицу продукции | Наличие ресурса | |||
Рекомендуемые материалы-66% Колебания линейной системы с одной степенью свободы Домашнее задание Вариант 19 - ДЗ ДЗ вариант 9 (ворд и маткад с графиками) "Предприятие «Химия» решает освоить выпуск стирального порошка .." FREE ДЗ - Титульный лист Крипотовалюты/экономика П1 | П2 | П3 | П4 | ||
| Р1 Р2 Р3 | 1 0 4 | 0 1 2 | 2 3 0 | 1 2 4 | 180 210 800 |
| Цена единицы продукции | 9 | 6 | 4 | 7 |
Решение. Пусть x1, x2, x3, x4 – число единиц продукции соответствующего вида П1, П2, П3, П4, запланированных к производству. Поскольку имеются ограничения на размеры допустимых затрат ресурсов, то переменные x1, x2, x3, x4 должны удовлетворять системе неравенств:
 (1)
(1)
По смыслу задачи переменные удовлетворяют условию неотрицательности:
x1, x2, x3, x4 ³ 0 (2)
Суммарная прибыль от реализации продукции составит:
F = 9 x1 + 6 x2 + 4 x3 + 7 x4 (3)
Итак, требуется найти такой план выпуска продукции X = (x1, x2, x3, x4), удовлетворяющий системе (1) и условию (2), при котором функция (3) принимает максимальное значение.
Экономико-математическая модель задачи описывается средствами табличного процессора Excel как совокупность формул, сведенных в таблицу и зависящих от изменяемых параметров – исходных данных.
Для решения нашей задачи создадим в Excel «книгу» с именем «Оптимизация доходов предприятия». Данные занесем на лист, который назовем «План выпуска продукции», как показано на рис. 9.
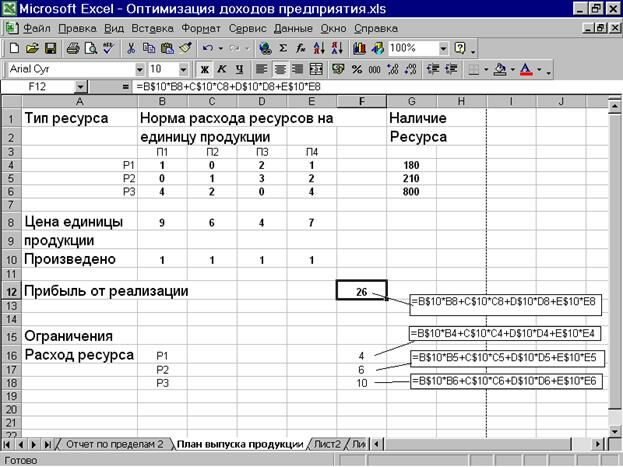
Рис. 9 Лист Excel с данными задачи
В ячейках B10, C10, D10 и E10 занесены предварительные значения переменных, которые будут варьироваться в процессе решения. Здесь они заданы равными единице, поскольку при решении линейных задач от начальных значений переменных не зависят ни конечные значения, ни время поиска решения.
В восьмой строке занесены коэффициенты целевой функции.
В ячейке F12 занесена формула для прибыли от реализации продукции.
В ячейках F16, F17, F18 занесены формулы для расхода ресурсов.
В Excel поиск значений переменных, при которых достигается экстремум целевой функции, осуществляется через пункт меню «Сервис », подпункт «Поиск решения » (в англоязычном варианте – «Solver »).
Раскройте пункт меню «Сервис », выберите команду «Поиск решения ». Если в меню «Сервис» отсутствует команда «Поиск решения », выберите команду «Сервис – Надстройки » и активизируйте надстройку «Поиск решения ».
"Поиск решения" вызывает диалоговое окно, представленное на рис. 10.
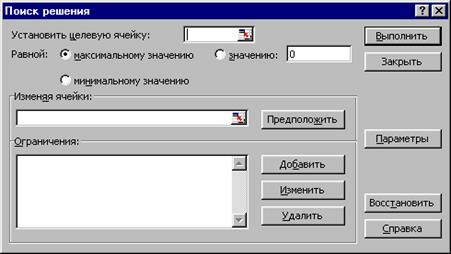
Рис. 10 Диалоговое окно «Поиск решения»
Ниже перечислены основные поля и органы управления диалогового окна «Поиск решения» и их назначение.
· Поле «Установить целевую ячейку» служит для указания ячейки, содержащей целевую функцию, значение которой необходимо максимизировать, минимизировать или установить равным заданному числу. (Эта ячейка должна содержать формулу).
· Переключатель «Равной» служит для выбора варианта оптимизации значения целевой ячейки (максимизация, минимизация или подбор заданного значения). Чтобы установить заданное значение, введите его в поле, расположенное справа от слова «Значение».
· Поле «Изменяя ячейки» служит для указания ячеек, значения которых изменяются в процессе поиска решения до тех пор, пока не будут выполнены наложенные ограничения и условие оптимизации значения ячейки, указанной в поле «Установить целевую ячейку».
· Кнопка «Предположить» используется для автоматического поиска ячеек, влияющих на формулу, ссылка на которую дана в поле «Установить целевую ячейку». Результат поиска отображается в поле «Изменяя ячейки».
· Список «Ограничения» служит для отображения списка граничных условий поставленной задачи.
· Кнопка «Добавить» служит для отображения диалогового окна «Добавить ограничение», с помощью которого записываются выражения, определяющие ограничения.
· Кнопка «Изменить» служит для отображения диалогового окна «Изменить ограничение», которое позволяет редактировать выбранное выражение из списка ограничений.
· Кнопка «Удалить» служит для снятия выбранного ограничения.
· Кнопка «Выполнить» служит для запуска поиска решения поставленной задачи.
· Кнопка «Закрыть» служит для выхода из окна диалога без запуска поиска решения поставленной задачи. При этом сохраняются установки, сделанные в окнах диалога, появлявшихся после нажатий на кнопки «Параметры», «Добавить», «Изменить» или «Удалить».
· Кнопка «Параметры» служит для отображения диалогового окна «Параметры поиска решения», в котором можно загрузить или сохранить оптимизируемую модель и указать предусмотренные варианты поиска решения. В данном случае под моделью понимается диапазон ячеек листа, в которых содержатся исходные данные, формулы и целевая ячейка, которые описывают решаемую задачу.
· Кнопка «Восстановить» служит для очистки полей окна диалога и восстановления значений параметров поиска решения, используемых по умолчанию.
Описание ограничений, присущих оптимизационной задаче, выполняется с помощью двух однотипных диалоговых окон «Добавление ограничения » и «Изменение ограничения », одно из которых представлено на рис. 11.
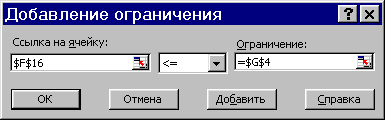
Рис. 1 Диалоговое окно «Добавление ограничения»
Ниже перечислены основные поля и органы управления названных диалоговых окон.
· Поле «Ссылка на ячейку» служит для указания ячейки или диапазона, на значения которых необходимо наложить ограничение.
· Раскрывающийся список предназначен для выбора условия (<=, >=, =) определяющего ограничение.
· Поле «Ограничение» служит для задания числа, формулы, ссылки на ячейку или диапазон, определяющие ограничение.
· Кнопка «Добавить » используется для того, чтобы, не возвращаясь в окно диалога «Параметры поиска решения», наложить новое условие на поиск решения задачи.
Управление алгоритмом поиска и определение его параметров (скорости сходимости, точности и т.п.) выполняется с помощью диалогового окна «Параметры поиска решения », представленного на рис. 12.
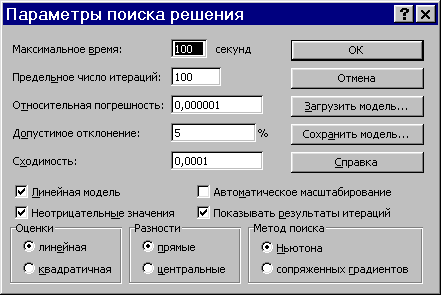
Рис. 12 Диалоговое окно «Параметры поиска решения»
В этом окне можно изменять условия и варианты поиска решения для линейных и нелинейных задач, а также загружать и сохранять оптимизируемые модели. Значения и состояния элементов управления, используемые по умолчанию, подходят для решения большинства задач.
Ниже описаны значения полей, переключателей и флагов этого диалогового окна:
· Поле «Максимальное время » служит для ограничения времени, отпускаемого на поиск решения задачи. В поле можно ввести время (в секундах), не превышающее 32767; значение 100, используемое по умолчанию, подходит для решения большинства простых задач.
· Поле «Предельное число итераций » служит для управления временем решения задачи путем ограничения числа промежуточных вычислений. В поле можно ввести количество итераций, не превышающее 32767; значение 100, используемое по умолчанию, подходит для решения большинства простых задач.
· Поле «Относительная погрешность » служит для задания точности, с которой определяется соответствие ячейки целевому значению или приближение к указанным границам. Поле должно содержать число из интервала от 0 до 1. Относительная погрешность по умолчанию 0,000001.
· Поле «Допустимое отклонение » служит для задания допуска на отклонение от оптимального решения, если множество значений влияющей ячейки ограничено множеством целых чисел. При указании большего допуска поиск решения заканчивается быстрее.
· Поле «Сходимость ». Когда относительное изменение значения в целевой ячейке за последние пять итераций становится меньше числа, указанного в поле «Сходимость», поиск прекращается. Сходимость применяется только к нелинейным задачам, условием служит дробь из интервала от 0 до 1.
· Флаг «Линейная модель » служит для ускорения поиска решения линейной задачи оптимизации или линейной аппроксимации нелинейной задачи.
· Флаг «Показывать результаты итераций » служит для приостановки поиска решения для просмотра результатов отдельных итераций.
· Флаг «Автоматическое масштабирование » служит для включения автоматической нормализации входных и выходных значений, качественно различающихся по величине, например, максимизация прибыли в процентах по отношению к вложениям, исчисляемым в миллионах рублей.
· Флаг «Значения не отрицательны » позволяет установить нулевую нижнюю границу для тех влияющих ячеек, для которых она не была указана в поле "Ограничение" диалогового окна «Добавить ограничение».
· Переключатель «Оценки » служит для указания метода экстраполяции (линейная или квадратичная), используемого для получения исходных оценок значений переменных в каждом одномерном поиске.
· Значение переключателя «Линейная» служит для использования линейной экстраполяции вдоль касательного вектора.
· Значение переключателя «Квадратичная» служит для использования квадратичной экстраполяции, которая дает лучшие результаты при решении нелинейных задач и не играет роли для линейных задач.
· Переключатель «Производные» служит для указания метода численного дифференцирования и для линейных задач его значение не играет роли.
· Переключатель «Метод поиска» служит для выбора алгоритма оптимизации (метод Ньютона или метод сопряженных градиентов) для указания направления поиска. Для решения задач линейного программирования его значения несущественны.
· Кнопка «Загрузить модель» служит для отображения на экране диалогового окна «Загрузить модель», в котором можно задать ссылку на область ячеек, содержащих загружаемую модель.
· Кнопка «Сохранить модель» служит для отображения на экране диалогового окна «Сохранить модель», в котором можно задать ссылку на область ячеек, предназначенную для хранения модели оптимизации. Данный вариант предусмотрен для хранения на листе более одной модели оптимизации, первая модель сохраняется автоматически.
В результате заполнения всех полей и внесения всех ограничений, диалоговое окно «Поиск решения» для нашей задачи примет вид рис. 13.
После нажатия на кнопку «Выполнить» появляется окно «Результаты поиска решения» , в котором предлагается выбрать тип отчета: результаты, устойчивость, пределы, либо любую их комбинацию. Переключатель «Сохранить найденное решение», либо «Восстановить исходные значения». Кнопки «ОК», «Отмена», «Сохранить сценарий» и «Справка».
После нажатия кнопки «ОК» к книге добавляются по листу на каждый из выбранных типов отчета: «Отчет по результатам», «Отчет по устойчивости» и «Отчет по пределам».
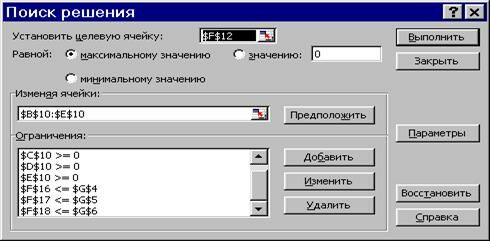
Рис. 13 Результат заполнения полей диалогового окна «Поиск решения»
Ниже приведено описание листов отчетов для нашей задачи и экономическая интерпретация результатов решения.
1. «Отчет по результатам» (рис. 14) состоит из трех таблиц:
· в таблице «Целевая ячейка (Максимум)» приведены адрес, исходное и результатное значение целевой функции;
· в таблице «Изменяемые ячейки» находятся адреса, идентификаторы (имена) и значения всех искомых переменных задачи;
· в таблице «Ограничения» показаны результаты оптимального решения для ограничений задачи. В графе «Формула» указаны зависимости, которые были введены в диалоговом окне «Поиск решения».
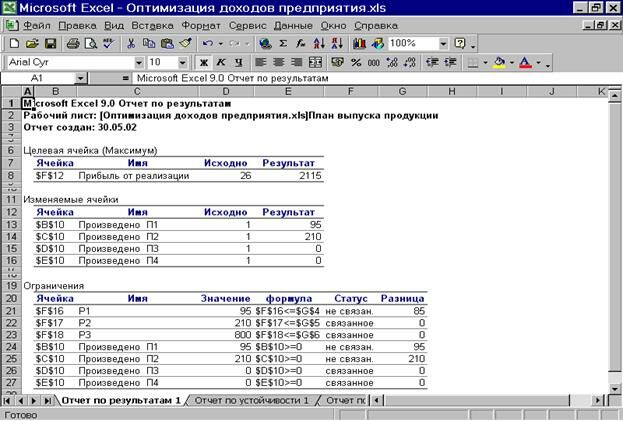
Рис. 14 Лист отчета по результатам
В результате 4-х итераций получен оптимальный план производства
X*=(95; 210; 0; 0), максимальное значение целевой функции (прибыль от реализации продукции) составляет 2115 денежных единиц.
· В таблице «Ограничения» этого листа приводятся значения левых частей каждого ограничения задачи ЛП; разница между значениями правых и левых частей по каждому ограничению.
Исходя из экономического смысла, каждая разница представляет собой разность между запасами соответствующего ресурса и его потреблением.
В нашей задаче ресурсы второго и третьего типов (Р2 и Р3) использованы полностью, а соответствующие им ограничения системы (1) обратились в точные равенства при подстановке оптимального плана в систему ограничений экономико-математической модели задачи. (Эти ограничения имеют статус «связанное»).
Ресурс 1-го типа (Р1) используется в оптимальном плане в объеме 95 единиц, а значит, остается в избытке в объеме, равном 85 единиц. И соответствующее ограничение системы (1) имеет вид строгого неравенства при подстановке оптимального решения. Это ограничение имеет статус «несвязанное».
2. «Отчет по устойчивости» (рис. 15) содержит информацию о том, насколько целевая ячейка чувствительно к изменениям ограничений и переменных. Этот отчет имеет две таблицы: одна для изменяемых ячеек, вторая для ограничений.
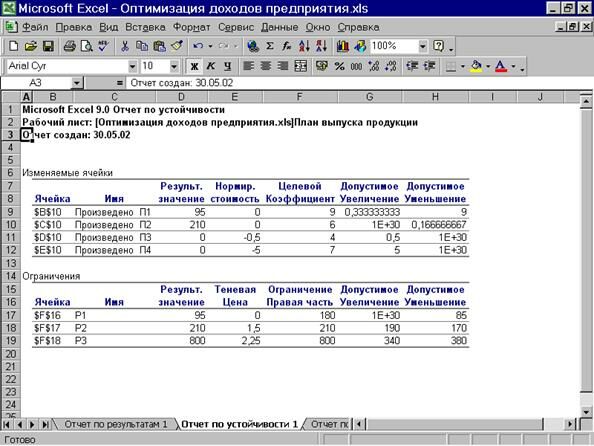
Рис. 15 Лист отчета по устойчивости
· В таблице «Изменяемые ячейки» , графа «Нормир. стоимость» содержит значения дополнительных двойственных переменных, показывающих возможности изменения целевой функции.
Графа «Целевой коэффициент» показывает степень зависимости между изменяемой и целевой ячейками, то есть коэффициенты целевой функции.
Графы «Допустимое увеличение» – «Допустимое уменьшение» показывают предельные значения приращения коэффициентов в целевой функции, при которых сохраняется оптимальное решение.
· В таблице «Ограничения» , в графе «Теневая цена» приведены двойственные оценки, которые показывают, как изменится максимальное значение целевой функция при изменении запаса ресурса на единицу.
В графах «Допустимое увеличение» – «Допустимое уменьшение», показаны предельные значения изменения запаса каждого ресурса, при которых сохраняется набор переменных, входящих в оптимальное решение.
Пользуясь отчетом по устойчивости можно провести послеоптимизационный анализ задачи линейного программирования, основанный на двойственных оценках, а именно:
Ø проводить анализ чувствительности коэффициентов целевой функции к изменению исходных данных;
Ø определить степень дефицитности ресурсов;
Ø установить, как изменится максимальное значение целевой функции при изменении запасов ресурсов на единицу.
· В таблице «Изменяемые ячейки» приведены результирующие значения для каждой переменной, а в графе «Нормир. стоимость» приведены значения, показывающие насколько затраты по производству превышают цену реализации этого вида продукции.
По оптимальному плану в рассмотренной задаче следует производить продукцию первого и второго видов и превышение затрат над ценой реализации равно нулю. Например, для продукции первого вида затраты на ресурсы составляют 1×y1 + 0×y2 + 4×y3 = 1×0 + 0×1,5 + 4×2,25 = 9 и цена реализации равна 9.
А для продукции, например, третьего вида затраты на ресурсы составляют 2×y1 + 3×y2 + 0×y3 = 2×0 + 3×1,5 + 0×2,25 = 4,5. Цена реализации этой продукции равна 4, и соответствующая нормированная стоимость равна 0,5. Если включить в план производства единицу продукции третьего вида, то целевая функция уменьшится на 0,5 денежных единиц, поэтому в таблице нормированная стоимость указана со знаком минус.
В оптимальный план производства попадают только рентабельные, неубыточные виды продукции. Критерием рентабельности здесь считается равенство цены и затрат на производство продукции.
· В таблице «Изменяемые ячейки» для каждого коэффициента целевой функции указано его исходное значение, а также, на какое предельное значение
можно увеличить, либо уменьшить этот коэффициент с сохранением оптимального плана.
Например, цена первого вида продукции может быть увеличена на 0,33 или уменьшена на 9, как видно из таблицы. Для продукции третьего вида увеличение цены более, чем на 0,5 приведет к тому, что она станет рентабельной и ее необходимо будет ввести в оптимальный план выпуска продукции.
· В таблице «Ограничения» для каждого вида ресурса указано, какое количество его используется в оптимальном плане (графа «Результ. значение»), а в графе «Теневая цена» приведены двойственные оценки ресурсов. В литературе эти оценки называют «скрытыми доходами», «маргинальными оценками», «разрешающими множителями» или «объективно обусловленными оценками» (по Л. В. Канторовичу). Эти оценки показывают, насколько денежных единиц изменится максимальная прибыль от реализации продукции при изменении запаса соответствующего ресурса на одну единицу.
Ресурс, использованный в оптимальном плане не полностью, называется недефицитным и получает нулевую двойственную оценку, в отличие от ресурсов, использованных полностью.
В этой же таблице указано для каждого вида ресурса его исходное значение (графа «Ограничение Правая часть»), а также, на какое предельное значение можно увеличить или уменьшить запас каждого ресурса, с сохранением структуры оптимального плана. Например: при увеличении запаса второго ресурса Р2 на величину 190 либо уменьшении на 170 единиц, набор производимой продукции (базисных переменных) останется неизменным.
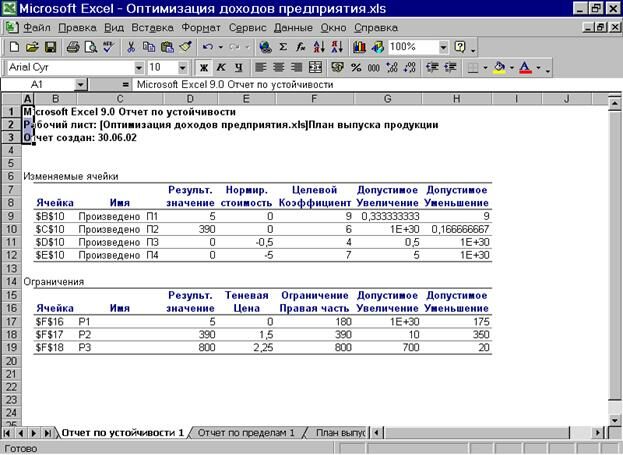
Рис.16 Лист отчета по устойчивости с измененными ресурсами
Проверим данное утверждение, изменив величину запаса второго ресурса с 210 единиц до 390. Рис. 16 показывает, что при этом производимая продукция осталась той же, нормированные стоимости и теневые цены не изменились. Допустимое увеличение запасов второго ресурса сократилось до 10, то есть максимальное его значение по-прежнему 400.
3. «Отчет по пределам» (рис. 17). В лист “Отчета по пределам” кроме экстремального значения целевой функции для оптимального плана в графах «Нижний предел» и «Верхний предел» приведены возможные предельные значения переменных, а также соответствующие значения целевой функции.
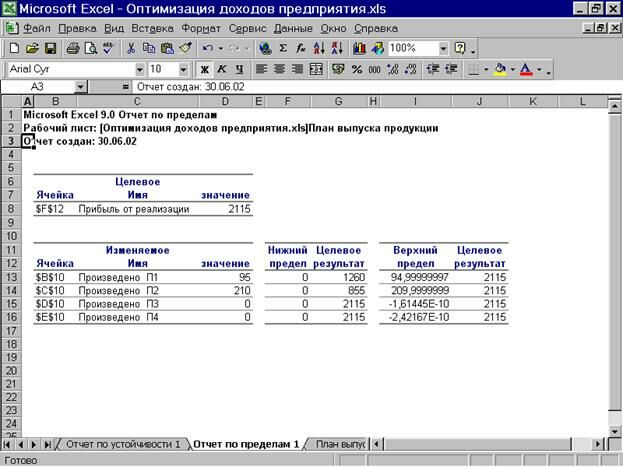
Рис. 17 Лист отчета по пределам
Таким образом, мы видим, что использование пакетов прикладных программ позволяет довольно полно провести послеоптимизационный анализ, и тем самым принять наиболее приемлемое и обоснованное решение.
В заключение приведем высказывание Эмерсона: «Приступайте к делу и силы появятся».
Желаем успеха!
Задача о составлении оптимального рациона питания
Пусть имеется m видов необходимых человеку витаминов S1, S2, …, Sm, содержащихся в n видах различных продуктов P1, P2, …, Pn.
Известны следующие исходные данные:
aij – содержание i-го витамина Si в j-ом продукте Pj;
cj - стоимость единицы продукта Pj;
bi - минимальная суточная потребность в i-м витамине.
Требуется составить оптимальный рацион питания из продуктов P1, P2, …, Pn с учетом суточной потребности в витаминах S1, S2, …, Sm, при котором затраты на продукты будут минимальными. Построим математическую модель этой задачи.
Обозначим за xj (j = 1,2,...,n) – количество каждого вида продукта в суточном рационе. Тогда затраты на продукты составят cj∙xj, а суммарные затраты на суточный рацион составят:
F = c1 x1 + c2 x2 + ...+ cn xn.
Естественно, хотелось бы понести минимальные затраты. Следовательно, они подлежат минимизации.
Общее количество витамина Si в потребленных продуктах Х = (x1, x2 ,..., xn ) будет выражаться суммой произведений содержания витамина aij на количество потребленного продукта и составит величину, равную ai1 x1 + ai2 x2 + ... + ain xn . Поскольку суточная потребность в витамине Si равна bi , а суточное потребление не должно быть меньше его необходимого количества, то приходим к ограничениям следующего вида:
ai1x1 + ai2x2 +… + ainxn  bi, i = 1,2,...,m
bi, i = 1,2,...,m
Учитывая естественные условия неотрицательности потребления продуктов,
xj 0, j=1,2,...,n,
0, j=1,2,...,n,
придем к следующей задаче:
Найти такой план Х = (x1, x2 ,..., xn) питания, удовлетворяющий системе неравенств
 a11x1 + a12x2 + … + a1nxn
a11x1 + a12x2 + … + a1nxn  b1,
b1,
a21x1 + a22x2 + … + a2nxn  b2,
b2,
… … … … … … …
ai1x1 + ai2x2 + … + ainxn  bi,
bi,
… … … … … … …
am1x1 + am2x2 + … + amnxn  bm,
bm,
xj ³ 0, j = 1, 2, …, n,
при котором функция F = c1x1 + c2x2 + … + cnxn принимает минимальное значение.
В десяти видах продуктов (P1, P2, Р3, Р4, Р5, Р6, Р7, Р8, Р9, Р10) содержатся 5 видов витаминов (S1, S2, S3, S4, S5). Минимальная суточная потребность человека в этих витаминах равна соответственно b1, b2, b3, b4, b5 мг. Содержание витамина i-го вида (i = 1, 2, 3, 4, 5) в продукте j-ого вида (j = 1, 2, 3, 4, 5, 6, 7, 8, 9, 10) составляет aij мг в 100 г продукта. Цена 100 г продукта равна cj рублей.
| Витамины | Продукты | Суточная потреб-ность | |||||||||
| Хлеб ржаной | Курица | Говяди-на | Молоко | Карто-фель | Капуста свежая | Огурцы | Помидо-ры | Яблоки | Апель-сины | ||
| А | 0,00 | 0,00 | 0,04 | 0,10 | 0,02 | 0,02 | 0,06 | 2,00 | 0,09 | 0,30 | 1,50 |
| В1 | 0,15 | 0,16 | 0,20 | 0,05 | 0,07 | 0,14 | 0,06 | 0,07 | 0,04 | 0,06 | 1,50 |
| В2 | 0,07 | 0,16 | 0,17 | 0,17 | 0,04 | 0,07 | 0,01 | 0,04 | 0,04 | 0,03 | 2,00 |
| РР | 0,90 | 6,90 | 6,40 | 0,08 | 5,50 | 4,50 | 8,00 | 16,50 | 3,50 | 0,00 | 15,00 |
| С | 0,00 | 0,00 | 2,00 | 1,00 | 10,00 | 30,00 | 5,00 | 40,00 | 7,00 | 40,00 | 50,00 |
| Цена продукта | 2,00 | 8,00 | 17,00 | 2,10 | 1,80 | 3,50 | 5,00 | 6,00 | 4,50 | 4,50 |
Определить, сколько продуктов каждого вида следует потреблять в сутки, если человеку необходимо минимизировать свои затраты.
Решение. Составим экономико-математическую модель задачи. Обозначим x1, x2, x3, x4, x5, x6, x7, x8, x9, x10 – количество продуктов соответствующего вида, входящих в рацион питания. Поскольку суточное потребление витаминов не должно быть меньше минимальной суточной потребности человека, то переменные x1, x2, x3, x4, x5, x6, x7, x8, x9, x10 должны удовлетворять системе неравенств:


 (1)
(1)
По смыслу задачи переменные удовлетворяют условию неотрицательности:
x1, x2, x3, x4, x5, x6, x7, x8, x9, x10 ³ 0. (2)
Суммарные затраты на продукты составят составит:
F = 2 x1 + 8 x2 + 17 x3 + 2,1 x4 + 1,8 x5 + 3,5 x6 + 5 x7 + 6 x8 + 4,5 x9 + 4,5 x10. (3)
Итак, требуется найти такой план рациона питания X = (x1, x2, x3, x4, x5, x6, x7, x8, x9, x10), удовлетворяющий системе (1) и условию (2), при котором функция (3) принимает минимальное значение.
Формулировка двойственной задачи
Предположим, что некоторая организация решила закупить ресурсы Р1 , Р2 ,…, Рm фирмы и необходимо определить цены на эти ресурсы у1, у2,…, уm. Естественно, что покупающая организация заинтересована в том, чтобы затраты на покупку ресурсов в объеме b1, b2,…, bm по ценам у1, у2,…, уm были минимальны, то есть Z = b1y1 + b2y2 + … +bmym ® min.
Предприятие, продающее ресурсы, заинтересовано в том, чтобы полученная выручка была не меньше той суммы, которую предприятие может получить при переработке ресурсов в готовую продукцию. На изготовление единицы продукции j-го вида расходуется сырье Р1 в объеме а1j, сырье Р2 в объеме а2j…, сырье Рm в объеме аmj по цене у1, у2,…, уm соответственно, то есть затраты на изготовление продукции Пj должны быть не меньше, чем цена ее реализации. Приходим к ограничениям следующего вида:
а1jу1 + а2jу2 + … + аmjуm ≥ сj , j=1,2,...,n.
Учитывая условия неотрицательности цены единицы i-го ресурса, приходим к следующей задаче:
Найти такой вектор У = (у1, у2 ,..., уm) – цен ресурсов, удовлетворяющий системе неравенств
 a11у1 + a21у2 + … + am1уm ≥ c1,
a11у1 + a21у2 + … + am1уm ≥ c1,
a12y1 + a22y2 + … + am2ym ≥ c2,
… … … … … … …
a1jy1 + a2jy2 + … + amjym ≥ cj,
… … … … … … …
a1ny1 + a2ny2 + … + amnym ≥ cn,
yi ³ 0, i = 1, 2, …, m,
при котором функция Z = b1y1 + b2y2 + …+ bmym принимает минимальное значение.
Цены ресурсов в экономической литературе имеют различные названия: учетные, неявные, теневые, объективно-обусловленные оценки (о-о оценки). Смысл этих названий состоит в том, что это условные (ненастоящие) цены. Эти цены определяются в ходе решения задачи, их называют оценками ресурсов.
Сопоставим общие представления прямой и двойственной задач в табл. 3, причем прямая задача – это задача модели распределения ограниченных ресурсов.
Таблица 3
| Прямая задача | Двойственная задача |
| Максимизировать F = при ограничениях
xj ³ 0, j = 1, 2, …, n, | Минимизировать Z = при ограничениях
yi ³ 0, i=1,2,...,m |
Сравнивая рассмотренные примеры видно, что двойственная задача по отношению к исходной составляется согласно следующим правилам.
1. Если первая задача имеет размеры  (m–ограничений с n неизвестными), то вторая – размеры
(m–ограничений с n неизвестными), то вторая – размеры  .
.
2. Матрицы из коэффициентов при неизвестных в левых частях ограничений обеих задач являются взаимно транспонированными.
З. В правых частях ограничений в каждой задаче стоят коэффициенты при неизвестных в целевой функции другой задачи.
4. В прямой задаче все ограничения представляют собой неравенства типа « », причем в этой задаче требуется достичь
», причем в этой задаче требуется достичь  . Напротив, в двойственной задаче все ограничения суть неравенства типа «
. Напротив, в двойственной задаче все ограничения суть неравенства типа « », причем требуется достичь
», причем требуется достичь  .
.
Графически эти правила представлены в таблице 4.
Таблица 4
| Переменные двойственной задачи | Переменные прямой задачи | ||||||
| х1 | х2 | … | хi | … | xn | ||
| c1 | c2 | … | ci | … | cn | ||
| y1 y2 . . . yn | a11 a21 . . . am1 | a12 a22 . . . am2 | … … … … | a1i a2i . . . ami | … … … … | a1n a2n . . . amn | b1 b2 . . . bm |
| j-е ограничение двойственной задачи | коэффициенты целевой функции двойственной задачи |
Экономическое содержание основной теоремы двойственности состоит в следующем: если задача определения оптимального плана, максимизирующего выпуск продукции, разрешима, то разрешима и задача определения оценок ресурсов. Причем цена продукции, полученной при реализации оптимального плана, совпадает с суммарной оценкой ресурсов. Совпадение значений целевых функций для соответствующих планов пары двойственных задач достаточно для того, чтобы эти планы были оптимальными. Это значит, что план производства и вектор оценок ресурсов являются оптимальными тогда и только тогда, когда цена произведенной продукции и суммарная оценка ресурсов совпадают. Оценки выступают как инструмент балансирования затрат и результатов. Двойственные оценки обладают тем свойством, что они гарантируют рентабельность оптимального плана, то есть равенства общей оценки продукции и ресурсов и показывают убыточность всякого другого плана, отличного от оптимального.
Из приведенных соотношений видно, что для всех допустимых решений прямой и двойственной задач значения целевой функции задачи минимизации всегда будет верхним пределом значения целевой функции задачи максимизации. Таким образом, итерационное решение задачи максимизации ведет к возрастанию значения целевой функции, а итерационное решение задач минимизации – к ее убыванию. В итоге, при успешном завершении процессов вычисления прямой и двойственной задач приходят к точке «равновесия», где значения целевых функций задач максимизации и минимизации становятся равными.
Имеет место следующая теорема равновесия, используя которую можно находить решение одной из двойственных задач, зная решение другой задачи.
Теорема равновесия. Пусть Х* – какое-нибудь допустимое решение прямой задачи, а Y* – какое-нибудь допустимое решение двойственной задачи. Для одновременной оптимальности этих решений необходимо и достаточно выполнение равенств:
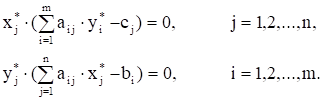
Величины, стоящие в скобках сформулированной теоремы, равны разности между левой и правой частями ограничения одной из двойственных задач на соответствующую переменную другой задачи.
Учитывая условия неотрицательности переменных и знаки сомножителей в произведениях, можно получить следующее:
если какое-либо ограничение одной задачи на оптимальном плане выполняется как строгое неравенство, то соответствующая координата оптимального плана другой задачи равна нулю:
Если Вам понравилась эта лекция, то понравится и эта - Италия после Первой Мировой Войны.
Если ai1 x1* + ai2 x2*+ ... + ain xn* < bi , то yi* = 0 .
Если a1j y1* + a2j y2*+ … + amj ym* > cj , то xj* = 0 .
Если какая-либо координата оптимального плана одной задачи положительна, то соответствующее ограничение другой задачи обращается в равенство:
Если yi* > 0 , то ai1 x1* + ai2 x2*+ ... + ain xn* = bi .
Если xj* > 0 , то a1j y1* + a2j y2*+ … + amj ym* = cj .
Экономическое содержание теоремы равновесия означает, что если по некоторому оптимальному плану Х* производства расход i-го ресурса строго меньше его запаса bi, то в оптимальном плане соответствующая двойственная оценка единицы этого ресурса равно нулю. Если же в некотором оптимальном плане оценок его i-ая координата строго больше нуля, то в оптимальном плане производства расход соответствующего ресурса равен его запасу. Отсюда следует, что двойственные оценки служат мерой дефицитности ресурсов. Дефицитный ресурс, который полностью используется по оптимальному плану производства, имеет положительную оценку, а избыточный ресурс, не используемый полностью, имеет нулевую оценку.



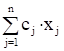
 ; i=1,2,...,m
; i=1,2,...,m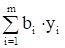
 ; j = 1, 2, …, n
; j = 1, 2, …, n


















