Расширенная a-игра
§ 4. Расширенная a – игра
Рассмотрим прямоугольную матрицу A размера n ´ m и отвечающую ей простую A–игру. Множества стратегий первого и второго игроков имеют вид
D = {d1, ¼, dn}, Q = {q1, ¼, qm}.
Назовем стратегии di чистыми стратегиями первого игрока, а qj – чистыми стратегиями второго игрока.
 Можно теперь расширить классы D, Q стратегий игроков, рассмотрев множества
Можно теперь расширить классы D, Q стратегий игроков, рассмотрев множества
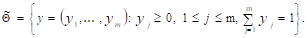 |
Вектор x = (x1, ¼, xn) будем называть смешанной стратегией первого игрока, понимая под этим следующее: в соответствии с этой стратегией первый игрок с вероятностью xi выбирает чистую стратегию di Î D. Аналогично интерпретируется смешанная стратегия y = (y1, ¼, ym) для второго игрока.
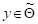
 Потери, которые понесет первый игрок, если он использует смешанную стратегию , а его оппонент смешанную стратегию , имеют вид
Потери, которые понесет первый игрок, если он использует смешанную стратегию , а его оппонент смешанную стратегию , имеют вид

где T означает транспонирование матрицы-строки y = (y1, ¼, ym), а запись xAyT понимается как произведение трех прямоугольных матриц в соответствии с обычными правилами умножения матриц.
Рекомендуемые материалы
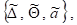 |
Расширенной A–игрой мы будем называть тройку
 где - классы смешанных стратегий первого и второго игроков соответственно, ã = ã(x, y) – функция потерь первого игрока вида (1).
где - классы смешанных стратегий первого и второго игроков соответственно, ã = ã(x, y) – функция потерь первого игрока вида (1).
 Обозначим
Обозначим
 Видно, что ã(x,) – максимальные потери, которые понесет первый игрок, если он будет следовать стратегии x; ã(¯, y) –минимальные потери, которые он понесет, если второй игрок выберет стратегию y.
Видно, что ã(x,) – максимальные потери, которые понесет первый игрок, если он будет следовать стратегии x; ã(¯, y) –минимальные потери, которые он понесет, если второй игрок выберет стратегию y.
 Определение 1. Число
Определение 1. Число
назовем верхней ценой расширенной A–игры.
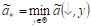 |
Определение 2. Число
назовем нижней ценой расширенной A–игры.
 Лемма 1. Имеет место следующее равенство
Лемма 1. Имеет место следующее равенство
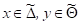
 Стратегии , удовлетворяющие неравенству
Стратегии , удовлетворяющие неравенству
называются оптимальными стратегиями, а (x, y, ã) – решением игры.
Лемма 2. Пусть число ã является ценой расширенной A–игры.
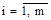
 1) Для того, чтобы стратегия была оптимальной, необходимо и достаточно, чтобы для
1) Для того, чтобы стратегия была оптимальной, необходимо и достаточно, чтобы для
 выполнялось неравенство:
выполнялось неравенство:
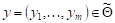
 2) Для того, чтобы стратегия была оптимальной, необходимо и достаточно, чтобы для
2) Для того, чтобы стратегия была оптимальной, необходимо и достаточно, чтобы для
 выполнялось неравенство:
выполнялось неравенство:
 Суть леммы 2 состоит в том, что нахождение оптимальной стратегии сводится к решению системы неравенств и равенств:
Суть леммы 2 состоит в том, что нахождение оптимальной стратегии сводится к решению системы неравенств и равенств:
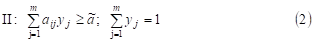 |
Лемма 3. Пусть число ã, стратегии x = (x1,¼, xn), y = (y1,¼, ym) удовлетворяют неравенствам (1), (2). Тогда они являются ценой игры и оптимальными стратегиями первого и второго игроков соответственно.
 Если для некоторого индекса j в (1) выполняется строгое неравенство, т.е. то соответствующий yj = 0.
Если для некоторого индекса j в (1) выполняется строгое неравенство, т.е. то соответствующий yj = 0.
 Если для некоторого индекса i в (2) выполняется строгое неравенство, т.е. то соответствующий xi = 0.
Если для некоторого индекса i в (2) выполняется строгое неравенство, т.е. то соответствующий xi = 0.
Доказательства этих лемм можно найти в [ ].
Задачи к § 4
 4.1. Рассмотреть А-игру с матрицей потерь первого игрока:
4.1. Рассмотреть А-игру с матрицей потерь первого игрока:
а) найти а*, а* и убедиться, что в простой А-игре нет цены;
б) составить систему линейных уравнений и неравенств для
ã, x = (x1, x2, x3), y = (y1, y2, y3)
в расширенной А-игре;
В лекции "4.9 Параметрические запросы" также много полезной информации.
в) найти решение ã, x, y в расширенной А-игре.
4.2. Для матрицы
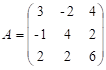 |
решить задачу 4.1.






















