§ 5. Основные типы систем массового обслуживания

Для описания СМО используется обозначение <×|×|×> (×).

Первое место в этом обозначении характеризует входной поток, а именно, характеризует распределение вероятностей промежутков поступлений между соседними клиентами.

Второе место является характеристикой обслуживающих приборов, а именно, характеризует распределение вероятностей времени обслуживания.

Третье место характеризует число обслуживающих приборов.

Четвертое место характеризует дисциплину очереди.

В основном мы будем изучать системы, когда в качестве распределения, стоящих на первом и втором местах, будет использоваться показательное распределение. Это связано с тем, что такие СМО адекватно описываются процессами гибели и размножения, которые мы изучали выше.  И, такие системы будут обозначаться следующим образом:

<M|M|m> (очередь длины N) или <M_l|M_m|m> (очередь длины N).

     Рассмотрим подробно некоторые известные системы.

1. Система <M|M|1> (с очередью)

Рекомендуемые материалы

Предположим, что X(t) – число клиентов в системе в момент t, и интенсивность поступления и обслуживания клиентов не меняется, т.е. l_k =l, k = 0, 1, ...   m_k = m, k = 1, 2, ... Диаграмма выглядит так:

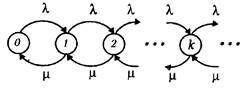Cоставляем систему дифференциальных уравнений для нахождения вероятности P_k(t) = P(X(t) = k). Для этого исследуем сходимость ряда

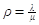Обозначим           .

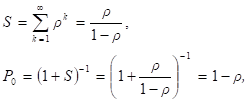 Если r < 1, то S < ¥ и стационарный режим существует. Если же r ³ 1, то S= ¥. Таким образом в данной системе стационарный режим существует тогда и только тогда, когда

В условиях существования стационарного режима найдем:

среднее число клиентов в системе:

среднее число клиентов в очереди:

Еще одной важной характеристикой системы является q – время ожидания начала обслуживания в стационарном режиме.

Лемма 1. Если r < 1, то вероятность того, что P(q ³ x) равна

Т.е. прежде чем начнут обслуживать, придется ждать как минимум x единиц времени. Отсюда можно получить (проверьте самостоятельно) среднее время ожидания начала обслуживания, или среднее время, проведенное в очереди:

Величина Eq является важной характеристикой «качества» обслуживания»: чем меньше Eq, тем обслуживание лучше.

Обозначим через Ev – среднее время, проведенное в системе:

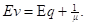Тогда

2. Система <M|M|m> (с очередью)

Пусть X(t) – число клиентов в системе в момент t. Предположим, что

Найдем условие стационарности. Для этого исследуем сходимость ряда S.

Если             , то S < ¥ и стационарный режим существует. Таким образом в данной системе стационарный режим существует тогда и только тогда, когда r < m.

В условиях существования стационарного режима

Предположим, что q – время, проведенное в очереди.

Лемма 2. При r < m вероятность того, что P(q ³ x) равна

 

 - вероятность того, что все приборы заняты.

Тогда среднее время, проведенное в очереди (проверьте самостоятельно)

3. Система <M|M|¥>

Это система, когда любому вновь прибывшему клиенту находят прибор.

Предположим, что l_k = l,  k = 0, 1, ¼; m_k = km,  k = 1, 2, ¼ Диаграмма выглядит так:

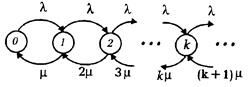
Найдем условие стационарности.

Т.е. независимо от того, какой r, стационарный режим существует всегда. Отсюда,

Для системы <М│М│∞> можно вывести формулы:(самостоятельно)

.

Также можно привести формулы для оценки P_k(t) и в случае, когда процесс еще не достиг стационарного режима.

, где  .

Как видно, и для неустановившегося режима X(t) подчиняется  пуассоновскому распределению. Очевидно, что EX(t) = α.

4. Ненагруженный резерв

 Пусть у нас имеется система, в которой основной элемент выходит из строя через λ-показательное время; вышедший из строя элемент немедленно заменяется новым, который был в резерве. Пусть в начальный момент времени исправных основных элементов было n. Обозначим через X(t) количество элементов, вышедших из строя к моменту t. Очевидно, что X(t) есть процесс чистого размножения, отвечающий диаграмме :

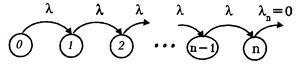Введем, как обычно, функции

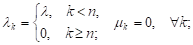
P_k(t) = P(X(t) = k),   k = 0,1,…,n.

Они удовлетворяют уравнениям

…………………………

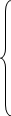
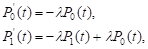
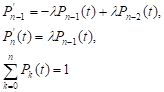
и начальному условию P₀(0) = 1.

Непосредственно проверяется, что

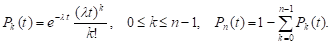
5. Нагруженный резерв

Пусть в предыдущей задаче все n элементов находятся в работе, выходя из строя по тому же λ-показательному закону. В этом случае процессу X(t) отвечает следующая диаграмма :

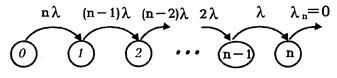
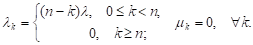
Функции P_k(t) удовлетворяют уравнениям

……………………………….

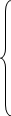
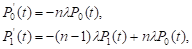
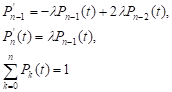
и начальному условию P₀(0) = 1.

Легко проверить, что

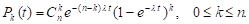
6. Система <М│М│1> (очередь ≤ N)

Эта система описывается процессом гибели и размножения X(t) с диаграммой :

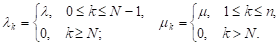
Очевидно, что при любом соотношении λ и μ существует стационарный режим и

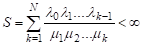
1) при ρ ≠ 1:

,

.

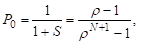
Можно вычислить также среднее число клиентов в системе в стационарном режиме:

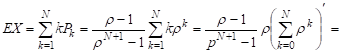
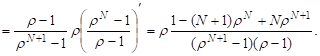
2) при ρ = 1

,

 

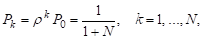
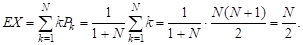
7. Система <М│М│m> (очередь ≤ N)

 Пусть X(t)  число клиентов в системе, характеристики этой системы:

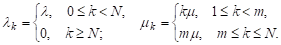
Напомним, что в этой системе длина очереди не может превышать N-m.

Найдем стационарные характеристики (они существуют). Пусть

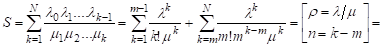
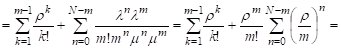
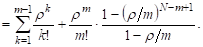
В случае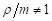

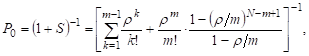
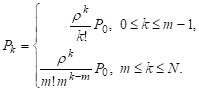
В случае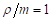

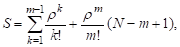
следовательно

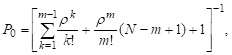
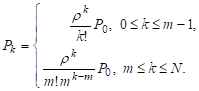
От системы <М│М│m> (с очередью) эта система отличается тем, что выражения для Р₀ не совпадают, и что ρ ≤ m – не обязательное условие для стационарности.

Можно найти

если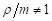

и  

если .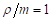

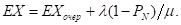
Среднее время, проведенное в очереди

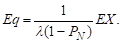
Здесь λ(1 - p_N )  – фактическое число клиентов, обслуженных в единицу времени, т.е. “эффективная” интенсивность входного потока. Иногда λ(1 - p_N ) обозначают через  λ_эфф.

8. Система <М│М│m> с ограниченным числом мест в очереди и ограниченным числом источника клиентов

Например, система, где бригада из m специалистов обслуживают N клиентов. Предполагается, что m<N (m механиков, N машин).Обозначим через λ – интенстивность возникновения обращения к специалисту (интенсивность возникновения неисправности) в расчете на одного клиента, то

 

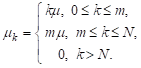
Приведем формулы (получите самостоятельно)

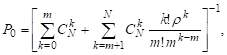
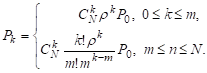
Для показателей EX_очер и EX:

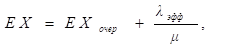где λ_эфф = λ(N - EX) - объясняется так: поскольку интенсивность поступления клиентов при наличие k клиентов равняется λ(N - k), где λ – интенсивность обращения к специалисту в расчете на одного клиента, то при условии стационарности

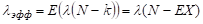
В частном случае, если m = 1, то получаем ситуацию, когда один обслуживающий прибор.

Задачи к § 5

5.1. На стоянке автомобилей имеется всего 10 мест, каждое из которых отводится под один автомобиль. Автомобили прибывают на стоянку в соответствии с пуассоновским потоком при средней частоте 10 автомобилей в час. Продолжительность пребывания автомобилей на стоянке распределена показательно со средним значением, равным 10 мин. Система работает достаточно долго. Найти вероятность того, что прибывший автомобиль не найдет на стоянке свободного места.

5.2. Клиенты прибывают к ларьку, в котором продаются прохладительные напитки, в соответствии с пуассоновским потоком при средней частоте 10 человек в час. Продолжительность обслуживания клиентов распределена показательно со средним значением 5 мин. Возле ларька имеются три места для ожидания, включая площадку для стоянки трех автомобилей. Другие подъезжающие к ларьку автомобили размещаются там, где есть свободное для стоянки место (в окрестности ларька). Система работает достаточно долго. Найти:

а) вероятность того, что прибывший к ларьку клиент имеет возможность занять очередь на площадке, отведенной для ожидания;

б) вероятность того, что прибывший клиент окажется вынужденным ждать за пределами площадки, специально отведенной для ожидания обслуживания;

в) среднюю длину интервала времени, в течении которого клиент окажется вынужденным ждать обслуживания;

г) число мест для размещения возле ларька автомобилей с учетом требования, которое заключается в том, чтобы доля среднего времени пребывания клиента в очереди составляла не менее 0,2 общего его пребывания в системе.

5.3. Пусть в системе <M|M|2> продолжительность обслуживания одного клиента равняется 5 мин., а средняя длина интервала времени между последовательными поступлениями заявок на обслуживание составляет 8 мин. Система работает достаточно долго. Найти:

а) вероятность возникновения задержки заявки в обслуживающей системе;

б) вероятность того, что хотя бы один из обслуживающих приборов будет незагруженным;

в) вероятность того, что незагруженным окажутся оба обслуживающих приборов.

5.4. Закусочная, расположенная около автомагистрали, имеет прилавок, возле которого может остановиться один автомобиль. По статистическим оценкам автомобили подъезжают к закусочной в соответствии с пуассоновским потоком со средней частотой 2 автомобиля за 5 мин. Подъездная дорожка к закусочной позволяет встать в очередь 10 автомобилям (очевидно, что если подъездная дорожка полностью занята очередью автомобилей, то дополнительно прибывающие к месту расположения закусочной автомобили могут расположиться для ожидания в каких-нибудь других местах). Для выполнения заказов клиентов требуется в среднем по 1,5 мин., и продолжительности обслуживания распределены по показательному закону. Требуется вычислить:

а) вероятность того, что у закусочной не окажется ни одного автомобиля;

б) среднее число ожидающих начала обслуживания клиентов;

в) среднее время ожидания от момента прибытия клиента до начала его обслуживания;

г) вероятность того, что количество прибывших к закусочной автомобилей превысит 10.

5.5. Рассмотрим работу пункта по обмену валюты. Клиенты приходят в пункт в соответствии с пуассоновским потоком в среднем каждые 6 минут. Время обслуживания одного клиента подчиняется показательному распределению со средним значением, равным 6 минутам. Каждый обслуженный клиент приносит доход в два доллара США (в среднем). Пункт имеет одну кассу обслуживания и два места для ожидания. Посетители, заставшие места для ожидания занятыми, теряются для системы. Для улучшения работы пункта рассматриваются два инвестиционных проекта:

Лекция "11 Принцип национального языка судопроизводства" также может быть Вам полезна.

а) затратив 200 долларов, оборудовать 4 места для ожидания (добавить еще два кресла);

б) затратив 1000 долларов, увеличить число мест для ожидания до 10.

Найти среднее время, за которое окупится каждый из этих проектов, если пункт работает 8 чесов в сутки.

5.6. Решить задачу 5.5. для случая, когда клиенты приходят в пункт в среднем каждые 12 минут в соответствии в пуассоновским потоком, а время обслуживания одного клиента то же.

5.7. Предположим, что имеются три проекта строительства морского порта: П1 - Построить два порта и в каждом порту соорудить один причал; П2 – Построить один порт с двумя причалами и П3 – Построить один порт с одним причалом, но с производительностью в два раза выше, чем в предыдущих проектах. Какому из проектов следует отдать предпочтение?

5.8. В системе с самообслуживанием входной поток является пуассоновским и имеет интенсивность, равная 50 клиентам в час. Продолжительность обслуживания в расчете на одного клиента распределена показательно со средним значением 5 минут. Определить: а) среднее число клиентов, находящихся в произвольно выбранный момент времени в стадии обслуживания; б) часть времени, в течение которого система простаивает