Адаптивная компенсация помех

48.Адаптивная компенсация помех.

Если амплитудно-фазовое соотношение по помеховому компоненту на выходах различных антенн различаются от аналогичных соотношений по сигнальному компоненту, то складывая с определенными весами выходные сигналы антенн можно обеспечить подавление помехового компонента.

Рассмотрим простейшую ситуацию когда одна из антенн направлена точно на источник помехи, а другая на источник сигнала, однако по боковым лепесткам принимает помеху.   

n₀(jω)= n_ип(jω)k₀(jω)

n₁(jω)= n_ип(jω)k₁(jω)

n₀(jω)-y(jω)=0

y(jω)=k_ф(jω)·n₁(jω)

Характеристики k₀(jω) и k₁(jω) описывают частотные характеристики трактов распространения помехи от источника помехи до А₀ и от источника помехи до А₁. Определим частотную характеристику адаптивного фильтра при которой на выходе вычитающего устройства происходит полное взаимное компенсация помех.

n_ип(jω)k₀(jω)-n_ип(jω) k₁(jω) k_ф(jω)=0

Рекомендуемые материалы

k_ф(jω)=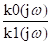

Эта система может подавлять любую помеху.(внеполосные и внутренние помехи)

Из полученного положения следует, что компенсация происходит независимо от формы помехи. Т.к. заранее характеристики k₀ и k₁ неизвестны и меняются во времени, то фильтр компенсатора помех должен быть адаптивным, и при его разработке решается задача выбора работы фильтра. Если фильтрацию обеспечивать по критерию минимума дисперсии выхода сигнала, то при этом обеспечивается наиболее глубокое подавление помехи.

Обозначим вых. Сигнал через Σ     Σ=S +-y

Дисперсия(усреднение по времени)   D_Σ=²=²+²+=²+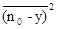

=0 за счет некоррелированности процессов S-сигнала и n-помехи;

Из этого следует, что минимум D_Σ достигается лишь при обеспечении min 2-ого слагаемого, что означает максимальную взаимную компенсацию процессов n₀ и y.

Рассмотрим простейшую реализацию адаптивного фильтра, когда он представляет собой звено с переменным коэффициентом передачи. Определим оптимальное значение коэффициента передачи, который обеспечивает минимум дисперсии сигнала на выходе.

Σ=S +-ωn    ω - коэффициент передачи фильтра;

D_Σ=²=²+²

=0     =ω_опт²       ω_опт==**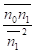

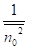
"3.1. Архитектурные особенности ОС" - тут тоже много полезного для Вас.

=ρ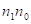

Оптимальные значения коэффициента передачи фильтра определяется степенью коррелированности процесса n₀ n_1, а также отношением их среднеквадратических значений. Определим степень подавления помехи при использовании данного адаптивного фильтра.

D_Σ=(S+-ω_опт)²=-²-2ω_опт+ω_опт² =+²-2+=

=+²-=+²(1-)

D_Σ= +²(1-g)

Если процессы  и   жестко коррелированны, то ρ=0, при этом обеспечивается полное подавление помехи. Если же эти процессы некоррелированы, то подавление помехи отсутствует.