Динамический анализ рычажных механизмов

5. Динамический анализ рычажных механизмов

5.1. Классификация действующих сил

         Среди сил, действующих на механизм, различают:

    а) движущие силы F_д или моменты M_д, ускоряющие движение входных (начальных) звеньев и совершающие положительную работу. Например: силы давления газа на поршень в двигателе внутреннего сгорания, силы веса при опускании груза и т.д.

    б) силы сопротивления F_c или моменты М_с, замедляющие движение входных звеньев и совершающие отрицательную работу. Они могут быть силами полезного сопротивления, дающими производственный эффект, и силами вредного сопротивления не дающими такого эффекта. К первому типу относятся например, силы тяжести при подъеме груза, а ко второму типу – силы трения.

    в) силы реакции в кинематических парах F_ij, возникающие в опорах звеньев и являющиеся внутренними силами для механизма в целом и внешними для каждого отдельного звена.

    г) силы инерции F_и или моменты сил инерции M_и возникают при переменном движении звеньев механизма и могут быть как движущими, так и силами сопротивления (в зависимости от их направления относительно направления движения звеньев). Фактически эти силы действуют на тело, вызывающее ускорение другого тела. Однако, условное приложения сил инерции к ускоряемому телу позволяет рассматривать его в равновесии. Этот принцип – принцип Даламбера позволяет задачу динамики свести к статическому расчету.

Рекомендуемые материалы

         Силы инерции относятся к категории распределенных или так называемых массовых сил, которые как и другие аналогичные силы могут быть приведены к главному вектору и главному моменту (рис.21).

   F_и =-ma_s;    M_и=-J_S·ε; где m и J_S – масса и момент инерции звена относительно оси, про-ходящей через центр масс;

    a_S – ускорение центра масс;

    ε – угловое ускорение звена.

         Знаки (-) показывают, что направления F_и и М_и противоположны соответствующим ускорениям.

         Сила F_и  и момент М_и, могут быть заменены одной силой F_и^/=F_и, линия действия которой проходит через так называемый центр качаний (точка К на рис.21) на оси звена и отстоит от линии действия F_и на расстоянии h=М_и/F_и при замене М_и парой сил F_и^/.

5.2.  Приведение сил и масс в механизме

         Для исследования закона движения механизма его удобно заменить одним условным звеном – звеном приведения, имеющим закон движения аналогичного звена реального механизма.

         Все внешние силы, действующие на звенья при этом заменяются одной приведенной силой F_∑^пр или моментом М_∑^пр , мощности Р_∑^пр которых равны мощностям Р_i заменяемых сил F_i и моментов сил M_i, т.е.

                        Р_∑^пр=∑Р_i,   где Р_i=F_i·V_i·cos(F_iV_i)   или   Р_i=М_i·ω_i;

                        Р_∑^пр=F_∑^пр·V·cos(F_∑^прV)    или    Р_∑^пр=М_∑^пр·ω.

         Здесь V_i и V – скорости точек приложения соответствующих сил; ω_i и ω – угловые скорости i-го звена и звена приведения.

         Суммарную приведенную силу или момент удобно записывать в виде составляющих, например: М_∑^пр=∑М_Fi^пр+∑М_Мi^пр, где каждая составляющая определяется из соответствующего равенства мощностей:

                                   М_Fi^пр=F_i·V_i/ω·cos(F_iV_i)  -  для силы F_i;

                                   М_Мi^пр=М_i·ω_i/ω   -   для момента М_i;

    Пример кривошипно-ползунного механизма (рис.22):        М_∑^пр=М_F^пр+M_G^пр,

 где   М_F^пр=F·V_C/ω₁=F·l_AB·рс/pb;

         M_G^пр=G·V_S/ω₁·cos(G^{^}V_S)=G·l_AB·ps/pb.

         Здесь pb, pc, ps^|=ps·cos(G^{^}V_S) – вектора, взятые с плана скоростей (рис.22).

Как видно из формул, величина F^пр (М^пр) зависит лишь от соотношения скоростей, а не от их абсолютной величины, что позволяет для приведения сил использовать планы скоростей без учета их масштабов. Каждое i-ое звено механизма обладает массой m_i и моментом инерции J_i относительно  оси,  проходящей  через  центр  масс звена, при  этом  кинетическая  энергия  i-го  звена  плоского  механизма  равна:           

                                                 T_i=(m_i·V_i²/2)+J_i·ω_i²/2.

      Массы и моменты инерции всех звеньев механизма можно условно заменить некоторой массой m^пр, сосредоточенной в произвольно выбранной точке А звена приведения (рис.23, а) или некоторым моментом инерции   J^пр,     приписанным     звену 

                                          Рис. 23                                               приведения (рис.23, б).

         Замена должна производится из условия равенства кинетических энергий:

                                                            Т^пр=Т_мех=∑Т_i,

где   Т^пр=m^пр·V_A²/2   или   Т^пр=J^пр·ω²/2,

т.е.  m^пр=∑[m_i·(V_i/V_A)²+J_i·(ω_i/V_A)²] – при поступательном движении звена приведения.

      J^пр=∑[ m_i·(V_i/ω)²+J_i·(ω_i/ω)²] – при вращательном движении звена приведения.

      m^пр и J^пр являются функциями положения звена приведения, т.е. их величина может меняться при изменении положения звена в процессе его движения.

5.3. Уравнение движения машины

         Работу машины можно разбить на 3 периода:

1) период пуска (разгон);

2) период установившегося движения;

3) период остановки (выбега);

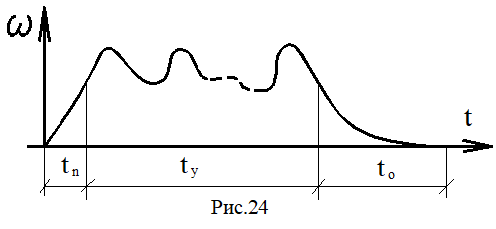         Аналитическая зависимость между действующими на звенья силами и кинематическими параметрами движения называется уравнением движения. Это уравнение в общем случае имеет вид ∆Т=А_д-А_с, где ∆Т=Т-Т₀ – изменение кинетической энергии за рассматриваемый промежуток времени (Т и Т₀ – величина кинетической энергии в конце и начале промежутка);

 А_д-А_с – суммарная работа действующих сил за рассматриваемый промежуток (А_д, А_с – работа движущих сил и сил сопротивления).

         В период пуска А_д-А_с=∆Т>0, т.е. происходит ускорение движения звеньев, являющегося неустановившемся.

         В период установившегося движения А_д-А_с=∆Т=0, т.е. скорости звеньев в конечный и начальный моменты цикла равны и вся работа движущихся сил расходуется на преодоление сопротивлений.

         В период остановки А_д-А_с=∆Т<0, движение продолжается некоторое время за счет накопленной кинетической энергии, поглощаемой за счет сопротивления движению.

         Уравнение движения может быть выражено в интегральной и дифференциальной форме, а для упрощения его решения исследование машины заменяют исследованием звена приведения, в котором изменение кинетической энергии равно:  ∆T^пр =А_д^пр-А_с^пр, где суммарная работа действующих на звено приведения сил может быть выражена:

      а) в интегральной форме:

                       А_д^пр-А_с^пр=∫F_∑^прds    или   А_д^пр-А_с^пр=∫M_∑^прdφ;

      б) в дифференциальной форме:

                              dT^пр=M_∑^прdφ    или    M_∑^пр=dT^пр/dφ;

т.е. при dT^пр=1/2·J^пр·ω²  получим:

M_∑^пр=(dJ^пр/dφ)·(ω²/2)+J^пр·ω·(dω/dφ)·(dt/dt)=(dJ^пр/dφ)·(ω²/2)+ε·J^пр.

         Таким образом, уравнение движения машины приводится к тому или иному конкретному виду и решается графическим и графоаналитическим методами, а учитываемые силы и моменты сил, а также приведенные массы и моменты инерции могут быть как постоянными так и переменными величинами, зависящими от того или иного фактора.

5.4. Понятие об уравновешивающей силе.

Теорема Жуковского о жестком рычаге

         Одним из способов определения приведенной силы F^пр является способ, предложенный проф. Н.Е. Жуковским. Уравнение, из которого может быть найдена F^пр, основано на равенстве мощностей:   F_∑^пр·V_A·cos(F_∑^пр V_A)=∑F_i·V_i·cos(F_i V_i).

         Рассмотрим какое-либо звено механизма, в т. В которого приложена сила F_i под углом α_i к вектору скорости V_i этой точки (рис.25, а).

        Мощность силы F_i равна:    

                    P_i=F_i·V_i·cosα_i.

        Если вектор скорости т. В (план скоростей) повернуть на

                                       Рис. 25                             90^˚ и силу F_i приложить к концу вектора (в т. «b»), сохранив ее направление, то момент этой силы относительно полюса «p» будет равен (рис.25, б):     M_i=F_i·h_i=F_i·V_i·cosα_i=P_i,

т.е. равен мощности силы F_i. Таким образом, F_i можно найти, повернув на 90^˚ план скоростей и приложив к нему все внешние силы, включая силы инерции, в соответствующих точках и сохраняя их направления. Тогда из уравнения моментов такого рычага:

 F_∑^пр·h_пр=∑F_i·h_i,  получим: F_∑^пр=∑F_i·h_i/h_пр, где h_i и h_пр – кратчайшие расстояния от полюса плана скоростей до линии действия i-ой и приведенной сил.

         Повернутый на 90^˚ план скоростей с приложенными к нему силами называется жестким рычагом Жуковского.

         Величина F^пр или М^пр зависит от положения механизма, поэтому можно построить диаграмму, например, F^пр(φ), являющуюся функцией положения звена приведения. Для этого необходимо последовательно определить значения F^пр методом рычага Жуковского для целого ряда положений механизма в пределах цикла (F₁^пр, F₂^пр,…) и отложить их на диаграмме (рис.26).

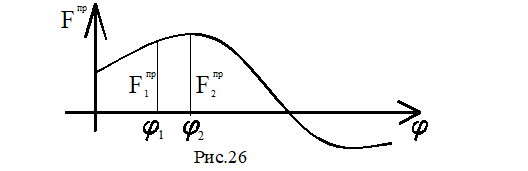
Приведенная сила F_∑^пр или момент М_∑^пр характеризует реакцию механизма на движение его входного звена по определенному закону, задаваемому двигателем. Сила или момент, равные по величине приведенной силе или моменту, но противоположные им по направлению называется уравновешенной силой F_ур или моментом М_ур. Эта сила или момент развивается двигателем и обеспечивает заданное движение входного звена.

         Если к рычагу Жуковского приложить все внешние силы, включая силы инерции, а также F_ур, то его можно рассматривать в равновесии, из условия которого:  F_ур·h_ур+∑F_i·h_i=0 можно определить неизвестную F_ур, а также найти мощность двигателя P_дв, требуемую для получения заданного движения входного звена в заданном положении:

                                        P_дв=F_ур·V_A·cos(F_урV_A)=M_ур·ω.

5.5. Графоаналитический метод решения уравнения движения машины

         Данный метод позволяет не только наглядно иллюстрировать связь между динамическими и кинематическими параметрами движения, но и решать практические задачи синтеза, например, задачу уменьшения неравномерности вращения звеньев.

         В качестве примера рассмотрим построение так называемой диаграммы энергомасс. Эта диаграмма строится на основе графиков:

                                 ∆Т^пр(φ)=Т^пр(φ)-Т₀^пр(φ)   и   J^пр(φ),

причем график ∆Т^пр(φ) может быть получен путем графического интегрирования графика М^пр(φ).

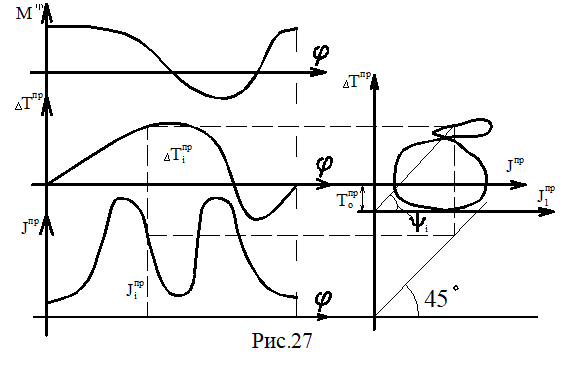
На рис.27 показана последовательность построения диаграммы энергомасс в координатах ∆Т^пр(J^пр), которая при установившемся движении является замкнутой кривой и строится на базе диаграмм ∆Т^пр(φ) и J^пр(φ) путем исключения параметра φ (φ – угол поворота звена приведения).

        Если известна угловая скорость вращения ω₀ звена приведения в начале цикла, то можно определить начальную кинетическую энергию:Т₀^пр=1/2·J₀^пр·ω₀².

         Тогда диаграмму энергомасс можно рассматривать в координатах Т^пр(J₁^пр), где ось J₁^пр отстоит от первоначальной оси J^пр на величину Т₀^пр (рис.27).

Так как Т^пр=1/2·J^пр·ω², то ω²=2·Т^пр/J^пр=2·μ_Т/μ_J·tgΨ,

где μ_Т и μ_J – масштабные коэффициенты, используемые для построения диаграмм. Таким образом, диаграмма энергомасс позволяет при установившемся движении определить угловую скорость ω звена приведения в любой момент времени, т.е.

                                     ω=;   а    tgΨ= μ_J/μ_T·ω²/2.

5.6. Неравномерное движение машин. Маховики

         Одним из режимов движения машины при совершении полезной работы является режим равномерного или установившегося движения.

       При равномерном движе-нии  угловая скорость ω вала  двигателя  постоянна, а при установившемся движении  она

                                     Рис. 28                               периодически изменяется (рис.28),

причём степень неравномерности можно оценить коэффициентом  неравномерности:                                                              

δ=(ω_max- ω_min)/ω_c,

где ω_с – средняя угловая скорость за цикл ω_с=(ω_max+ ω_min)/2.

Неравномерность вредно сказывается на работе машин, т.к. вызывает дополнительные инерционные нагрузки, которые могут привести к поломке.

         Практикой установлены значения δ, которые допустимы в различных условиях эксплуатации. Регулировать величину δ можно путем изменения величины момента инерции звена приведения, т.е. на быстро вращающийся вал закрепляется дополнительная масса, называемая маховиком.

         При конструировании маховика стремятся к получению необходимого момента инерции маховика J_м с наименьшим весом G и заданным диаметром D. Для этой цели маховик изготавливается в виде тяжелого обода, соединенного со втулкой тонким диском с отверстием или спицами (рис.29). Приближенно J_м можно определить по формуле:

                                                                                         J_м≈G·D²/40, кг·м·с².

5.7. Подбор момента инерции J_м маховика по заданному

 коэффициенту неравномерности δ

    Обычно требуется определить параметры маховика при заданных значениях ω_ср и δ. Существует два наиболее распространенных метода определения J_м – Н.И. Мерцалова и метод Ф. Виттенбауэра. Рассмотрим более точный метод Ф. Виттенбауэра, при котором предварительно строится диаграмма энергомасс ∆Т^пр(J^пр).                                                                                                                                    

Согласно этой диаграмме (рис.30):                                              ω²_max,min=2·μ_Т/μ_J·tgΨ_max,min,           

 tgΨ_max,min= μ_J/μ_T·ω²_max,min/2.

      С  другой  стороны  из  урав-нений п.5.6.:                                                 

        ω_max,min=ω_с·(1+(-)δ/2).

    Таким образом, найдя  Ψ_max и Ψ_min и проведя касательные к диаграмме энергомасс под этими углами к горизонтали (рис.30), получим в точке их пересечения начало новой системы координат

                               Рис. 30                                       с осями  Т  и  J₁^пр, отстоящими от

старых осей на искомую величину J_м и Т₀^пр.

       В целом последовательность определения J_м включает следующие операции:

1. Строится диаграмма М^пр(φ) для установившегося движения.

2. Строится диаграмма ∆Т^пр(φ) путем графического интегрирования диаграммы М^пр(φ).

3. Строится график J^пр(φ) и диаграмма энергомасс путем исключения параметра φ из графиков ∆Т^пр(φ) и J^пр(φ).

4. Определяются углы Ψ_max и Ψ_min, после чего находится J_м в новых координатах Т^пр и J₁^пр диаграммы Т^пр(J₁^пр).

5.8. Регулирование непериодических колебаний скорости движения машин

         В процессе выполнения работы приходится регулировать скорость рабочего органа машины. Например, в стационарных двигателях необходимо поддерживать скорость рабочего органа постоянной, а в двигателях транспортных машин эта скорость должна изменяться в широких пределах.

         Из уравнения движения машины следует, что изменения скорости рабочего органа можно достигнуть за счет изменения разности работ движущих сил и сил сопротивления (А_д-А_с). Устройства, обеспечивающие изменения работы сил сопротивления применяются в виде тормозов, например, в транспортных машинах, которые снабжаются также и приспособлениями для одновременного разобщения двигателя с машиной – орудием.

         Другим способом регулирования является изменение работы движущих сил путем воздействия на орган, подающий энергию к входному звену (поршню у двигателя внутреннего сгорания, лопаткам турбины и т.д.).

        

                                                                          

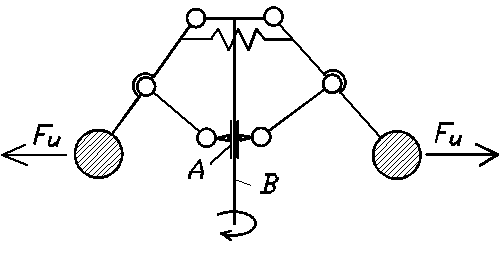
                                                  Рис. 31

Регулирование может осуществляться либо человеком-оператором, либо автоматически – с помощью устройств, называемых регуляторами.

         Одним из них является центробежный регулятор (рис.31), приводимый во вращение валом двигателя В. Ползун А соединяется с органом, подводящим рабочее тело (пар, горючая смесь и т.д.). Регулятор автоматически поддерживает скорость вала двигателя постоянной, т.к. ее увеличение приводит к уменьшению подачи рабочего тела и наоборот.

5.9. Силовой расчет рычажных механизмов

         Зная активные силы, действующие на звенья механизма и силы инерции этих звеньев, можно произвести его кинетостатический расчет, т.е. определить реакции в кинематических парах и уравновешивающую силу (момент) на входном звене, причем эта сила (момент) является движущей при совпадении ее направления с направлением движения входного звена или силой (моментом) сопротивления, если ее направление противоположно этому движению.

         При кинетостатическом расчете реакции в кинематических парах определяются путем статического расчета, который базируется на результатах кинематического анализа, включая ускорения, необходимые для определения сил (моментов) инерции.

         При силовом расчете используется принцип Даламбера, позволяющий решение задачи динамики свести к статическому расчету. Согласно этому принципу приведение ускоренно движущейся системы в равновесие обеспечивается условным приложением к этой системе сил инерции. При этом неизвестные силы определяются из уравнений статики.

    Силы взаимодействия между звеньями (реак­ции) можно считать направлеными   по  нор-­

мали  к контактирующим

поверхностям, если рас­чет ведется без учета сил тре­ния (рис.32, а, б).

                               рис. 32

При графоаналитическом решении используется метод плана сил. Механизм расчле­няется на структурные группы Ассура и начальные зве­нья. Расчет ведется, на­чиная с последней структурной группы и заканчивается рас­четом входного звена.

         При расчете структурных групп к ним прикладываются все действующие силы, включая силы инерции и реакции  отброшенных  связей.  Каждая  из  неиз-

вест­ных реакций, при необходимости, может быть разложена на две составляю­щие по выбранным направлениям, например, вдоль оси звена (нормаль­ная Fⁿ) и перпендикулярно оси (тангенциальная F^t). При равенстве числа уравнений статики числу неизвестных реакций их можно определить аналити­чески и графически, построив многоугольник (план) сил. Неизвестные опре­делятся из условия замкнутости векторной суммы сил. Рассмотрим при­меры:

1)

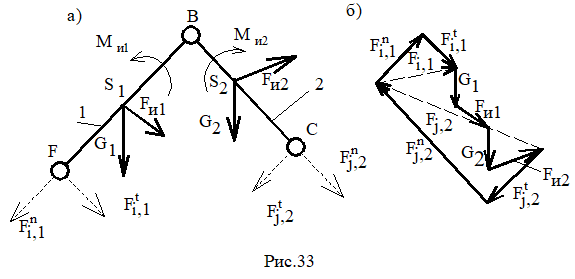Двухповодковая группа с вращательными парами:

         F_i,1^t определяется из уравнения моментов для звена 1 - ∑М_B=0 относи­тельно т. В. (рис.33, а);

         F_j,2^t определяется из уравнения моментов для звена 2 - ∑М_В=0 относи­тельно т. В (рис.33,а).

         При отрицательных значениях реакций необходимо изменить их направле­ния на противоположные.

         F_i,1ⁿ и F_j,2ⁿ определяются из плана сил (рис.33,б), полученного на основе вектор­ного уравнения;

         ∑F_k=0, где F_k – силы, действующие на структурную группу.

2)

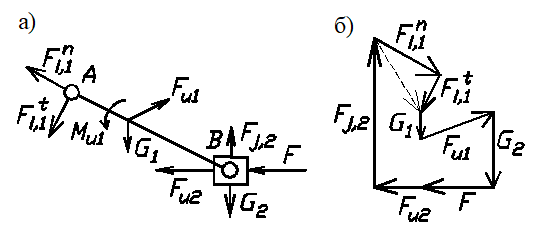Двухповодковая группа шатун-ползун (рис.34, а, б)

Рис. 34

       F_j,2 определяется из уравнения моментов - ∑М_А=0 относительно т. А. F_i,1=F_i,1ⁿ+F_i,1^t определяется из плана сил (рис.34,б) на основе векторного уравне­ния ∑F_k=0.

"6.1. Физическая организация жесткого диска" - тут тоже много полезного для Вас.

3) Двухповодковая группа кулиса-камень (рис.35, а)

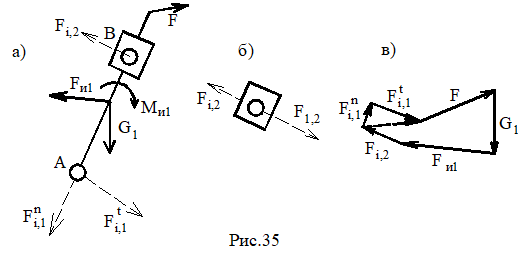      F_j,2 определяется из уравнения моментов - ∑М_А=0.

F_i,1=F_i,1ⁿ+F_i,1^t определяется из плана сил (рис.35, в), на основе векторного уравне­ния ∑F_k=0. При этом особенность расчета данной группы Ассура состоит в возмож­ности некоторого упрощения вычислений в случае, когда весом камня 2 можно пренебречь. Тогда реакция F_j,2 противоположна реакции F_1,2 и перпендику­лярна АВ, т.е. линия ее действия известна (рис.35, б).

4) Входное (начальное) звено (рис.36, а).

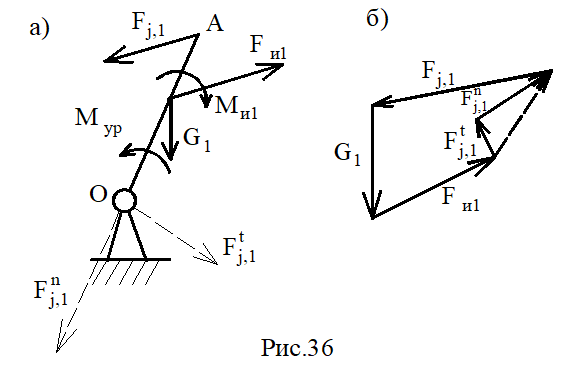     М_ур определяется из уравнения моментов - ∑М_о=0.

F_j,1=F_j,1ⁿ+F_j,1^t определяется из плана сил (рис.36,б) согласно векторному уравне­нию ∑F_k=0.