Вывод уравнений для плоских волн

ПОЛСКИЕ ВОЛНЫ

1. Вывод уравнений для плоских волн

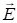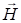Рассмотрим    электромагнитный    волновой    процесс,    векторы  и    которого могут быть представлены в виде

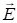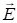                        =(x,t),  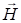  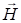              =(x,t)                                                    (1.1)                     

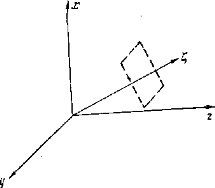
Рис.  1.1.   Направление  распространения плоской волны

Здесь (рис.   1.1.)     есть  расстояние   от   начала    координатной системы до плоскости

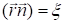
а  является постоянным  единичным  вектором. Так  как  производные по координатам будут равны   и т. д., то

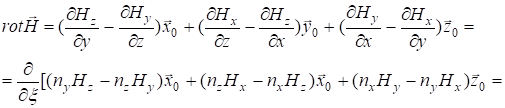
Рекомендуемые материалы

                                                   (1.2)

  (1.3)

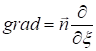
Следовательно, для плоской волны уравнения Максвелла принимают вид

                                                 (1.4)

,                      

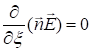Последние два уравнения означают независимость проекци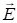й  и 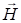 на направление распространения от координаты x, т. е. E_x =const и H_x=const в данный момент времени. Исследуем их по­ведение во времени. Для этого второе уравнение  (1.4)    умножим скалярно на :

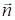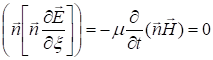
Так как

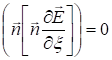
то

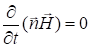
и

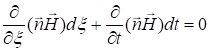
или , т.е.  dH_x = 0, H_x = const.   Для  исследования поведения E_x умножим скалярно  первое  из уравнений  (1.4)   на :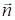

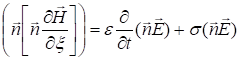
Так  как , получаем

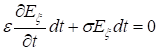
Прибавим к этому равенству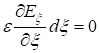

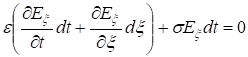
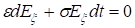
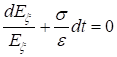
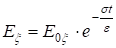
Следовательно, при конечной s компонента E_x экспоненциально убывает со временем, т. е. статическое электрическое поле не может поддерживаться внутри проводника.

Найдем уравнения для 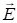 и 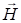отдельно. Для этого продиффе­ренцируем по t первое из уравнений (1.4)

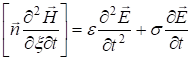
Найдем  из второго   из   уравнений   (1.4),   продифференцировав его по x:

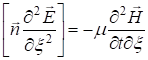
Получаем

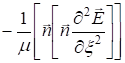
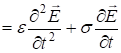
откуда

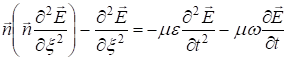
, так как

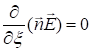
Отсюда следует

                                         (1.6)

Аналогично

                                                  (1.7)

Эти уравнения   можно   решить   методом   разделения   переменных, идем решение для комплексной амплитуды Е поля 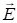, Положив

E=f₁(x)f₂(x)

Получаем

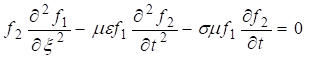
                (1.8)

Общее решение для f₁ будет

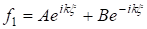
Частное решение для f₂ возьмем в виде

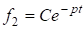
Таким образом, решением  для 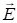 будет выражение

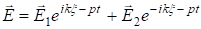
Решая уравнение (1.7), получим аналогичное решение для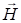

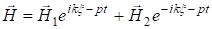
Подставив эти значения во второе из уравнений (1.4), получим

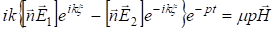
откуда

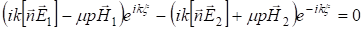
Так как x в этом равенстве может принимать   любые   значения,    коэффициенты при экспонентах должны равняться нулю:

Профессиональные требования к переводчику - лекция, которая пользуется популярностью у тех, кто читал эту лекцию.

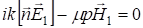
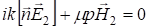
Поэтому

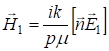
                                      (1.9)

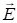
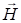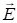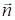
Отсюда следует  ()=0 (так как ([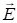])=0), т. е. векторы  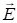и 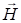ортогональны  к  направлению  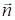и друг к другу.