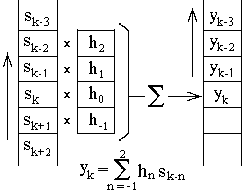Дискретные преобразования сигналов
Тема 6: дискретные преобразования сигналов
Нет ничего, сколь бы великим и изумительным оно не показалось с первого взгляда, на что мало-помалу не начинаешь смотреть с меньшим изумлением.
Лукреций. О природе вещей
Римский поэт и философ, I в.до н.э..
Преобразование всегда должно быть осознанным и целенаправленным действом. Был баран - стал шашлык. Что может быть прекраснее такого преобразования!
Виль Ибрагимов. Зри в корень.
Ташкентский геофизик Уральской школы, ХХ в.
Содержание: 6.1. Преобразование Фурье. Дискретные преобразования Фурье. Быстрое преобразование Фурье. 6.2. Преобразование Лапласа. 6.3. Z - преобразование сигналов. Определение преобразования. Связь с преобразованиями Фурье и Лапласа. Свойства z-преобразования. Отображение z-преобразования. Аналитическая форма z-образов. Обратное z-преобразование. 6.4. Дискретная конволюция (свертка). Уравнение дискретной свертки. Техника свертки. 6.5. Дискретные функции корреляции и спектры мощности. Литература.
6.1. Преобразование Фурье [5,17,21].
Рекомендуемые материалы
Дискретные преобразования Фурье могут быть получены непосредственно из интегральных преобразований дискретизаций аргументов (tk = kDt, fn = nDf):
S(f) = s(t) exp(-j2pft) dt, S(fn) = Dt
s(t) exp(-j2pft) dt, S(fn) = Dt s(tk) exp(-j2pfnkDt), (6.1.1)
s(tk) exp(-j2pfnkDt), (6.1.1)
s(t) = S(f) exp(j2pft) df, s(tk) = Df
S(f) exp(j2pft) df, s(tk) = Df S(fn) exp(j2pnDftk). (6.1.2)
S(fn) exp(j2pnDftk). (6.1.2)
Напомним также, что дискретизация функции по времени приводит к периодизации ее спектра, а дискретизация спектра по частоте - к периодизации функции. Для дискретных преобразований s(kDt) Û S(nDf) и функция, и ее спектр дискретны и периодичны, а числовые массивы их представления соответствуют заданию на главных периодах Т = NDt (от 0 до Т или от -Т/2 до Т/2, и 2fN = NDf (от -fN до fN), где N – количество отсчетов, при этом:
Df = 1/T = 1/(NDt), Dt = 1/2fN = 1/(NDf), DtDf = 1/N, N = 2TfN. (6.1.3)
Соотношения (6.1.3) являются условиями информационной равноценности динамической и частотной форм представления сигналов. Другими словами: число отсчетов функции и ее спектра должны быть одинаковыми. Но каждый отсчет комплексного спектра представляется двумя вещественными числами и, соответственно, число отсчетов комплексного спектра в 2 раза больше отсчетов функции? Это так. Но представление спектра в комплексной форме - не более чем удобное математическое представление спектральной функции, реальные отсчеты которой образуются сложением двух сопряженных комплексных отсчетов, а полная информация о спектре функции в комплексной форме заключена только в одной его половине - отсчетах действительной и мнимой части комплексных чисел в частотном интервале от 0 до fN, т.к. информация второй половины диапазона от 0 до -fN является сопряженной с первой половиной и никакой дополнительной информации не несет.
При дискретном представлении сигналов аргумент tk обычно проставляется номерами отсчетов k (по умолчанию Dt = 1, k = 0,1,…N-1), а преобразования Фурье выполняются по аргументу n (номер шага по частоте) на главных периодах. При значениях N, кратных 2:
S(fn) º Sn =  sk exp(-j2pkn/N), n = -N/2,…,0,…,N/2. (6.1.4)
sk exp(-j2pkn/N), n = -N/2,…,0,…,N/2. (6.1.4)
s(tk) º sk = (1/N) Sn exp(j2pkn/N), k = 0,1,…,N-1. (6.1.5)
Sn exp(j2pkn/N), k = 0,1,…,N-1. (6.1.5)
Главный период спектра в (6.1.4) для циклических частот от -0.5 до 0.5, для угловых частот от -p до p. При нечетном значении N границы главного периода по частоте (значения ±fN) находятся на половину шага по частоте за отсчетами ±(N/2) и, соответственно, верхний предел суммирования в (6.1.5) устанавливается равным N/2.
В вычислительных операциях на ЭВМ для исключения отрицательных частотных аргументов (отрицательных значений номеров n) и использования идентичных алгоритмов прямого и обратного преобразования Фурье главный период спектра обычно принимается в интервале от 0 до 2fN (0 £ n £ N), а суммирование в (6.1.5) производится соответственно от 0 до N-1. При этом следует учитывать, что комплексно сопряженным отсчетам Sn* в интервале 0-2fN соответствуют отсчеты SN-n.
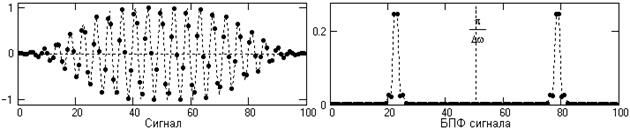
|
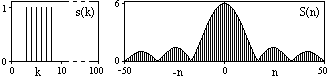
Рис. 6.1.1. Дискретный сигнал и модуль его спектра. |
Пример: На интервале Т={0,99}, N=100, задан дискретный сигнал s(k) = d(k-i) - прямоугольный импульс с единичными значениями на точках k от 3 до 8. Форма сигнала и модуль его спектра в главном частотном диапазоне, вычисленного по формуле S(n) =
d(k-i) - прямоугольный импульс с единичными значениями на точках k от 3 до 8. Форма сигнала и модуль его спектра в главном частотном диапазоне, вычисленного по формуле S(n) = s(k)×exp(-j2pkn/100) с нумерацией по n от -50 до +50 с шагом по частоте, соответственно, Dw=2p/100, приведены на рис. 6.1.1.
s(k)×exp(-j2pkn/100) с нумерацией по n от -50 до +50 с шагом по частоте, соответственно, Dw=2p/100, приведены на рис. 6.1.1.
|
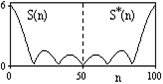
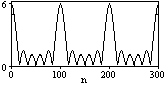
Рис. 6.1.2. Модуль спектра. Рис. 6.1.3. Модуль спектра. |
На рис. 6.1.2 приведена огибающая значений другой формы представления главного диапазона спектра. Независимо от формы представления спектр периодичен, в чем нетрудно убедиться, если вычислить значения спектра для большего интервала аргумента n с сохранением того же шага по частоте, как это показано на рис. 6.1.3 для огибающей значений спектра.
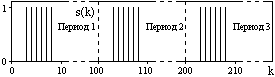
На рис. 6.1.4. показано обратное преобразование Фурье для дискретного спектра, выполненное по формуле s'(k) =(1/100) S(n)×exp(j2pkn/100), которое показывает периодизацию исходной функции s(k), но главный период k={0,99} этой функции полностью совпадает с исходным сигналом s(k).
S(n)×exp(j2pkn/100), которое показывает периодизацию исходной функции s(k), но главный период k={0,99} этой функции полностью совпадает с исходным сигналом s(k).
|
Рис. 6.1.4. Обратное преобразование Фурье дискретного спектра сигнала. |
Преобразования (6.1.4-6.1.5) называют дискретными преобразованиями Фурье (ДПФ). Для ДПФ, в принципе, справедливы все свойства интегральных преобразований Фурье, однако при этом следует учитывать периодичность дискретных функций и спектров. Произведению спектров двух дискретных функций (при выполнении каких-либо операций при обработке сигналов в частотном представлении, как, например, фильтрации сигналов непосредственно в частотной форме) будет соответствовать свертка периодизированных функций во временном представлении (и наоборот). Такая свертка называется циклической (см. раздел 6.4) и ее результаты на концевых участках информационных интервалов могут существенно отличаться от свертки финитных дискретных функций (линейной свертки).
Из выражений ДПФ можно видеть, что для вычисления каждой гармоники нужно N операций комплексного умножения и сложения и соответственно N2 операций на полное выполнение ДПФ. При больших объемах массивов данных это может приводить к существенным временным затратам. Ускорение вычислений достигается при использовании быстрого преобразования Фурье.
Быстрое преобразование Фурье (БПФ). В основе БПФ лежит прореживание по частоте и пирамидальный алгоритм, которым исключаются повторные вычисления периодически повторяющихся членов ряда Фурье.
Допустим, что массив чисел sk содержит N = 2r отсчетов (r - целое). Разделим исходный массив на два первых промежуточных массива с четными и нечетными отсчетами:
sk' = s2k, sk" = s2k+1, 0 £ k £ N/2-1.
Выполним ДПФ каждого массива с учетом того, что шаг функций равен 2 (при Dt=1), а период промежуточных спектров будет соответственно равен N/2:
sk' Þ Sn', sk" Þ Sn", 0 £ n £ N/2-1.
Для получения одной половины искомого спектра Sn сложим полученные спектры с учетом теоремы запаздывания, т.к. отсчеты функции sk" сдвинуты относительно sk' на один шаг дискретизации:
Sn = Sn'+Sn"×exp(-j2pn/N). (6.1.6)
Вторая половина спектра, комплексно сопряженная с первой, с учетом периода повторения N/2 промежуточных спектров определяется выражением:
Sn+N/2 = Sn'+Sn"×exp(-j2p(n+N/2)/N) = Sn'- Sn"×exp(-j2pn/N). (6.1.7)
Нетрудно видеть, что для вычисления полного спектра в данном случае потребуется N2/4 операций для вычисления промежуточных спектров плюс еще N операций комплексного умножения и сложения, что создает ощутимый эффект по сравнению с ДПФ.
Но деление массивов на две части может быть применено и к первым промежуточным массивам, и ко вторым, и т.д. до тех пор, пока в массивах не останется по одному отсчету, фурье - преобразование которых равно самому отсчету. Тем самым, алгоритм преобразования превращается в пирамидальный алгоритм перестановок со сложением/вычитанием и с единичным умножением на значение exp(-j2pn/N) соответствующего уровня пирамиды. Первый алгоритм БПФ на данном принципе (из множества модификаций, существующих в настоящее время) был разработан Кули-Тьюки в 1965 г. и позволил повысить скорость вычислений в N/r раз по сравнению с ДПФ. Чем больше N, тем больше эффект БПФ. Так, при N = 1024 имеем r = 10 и соответственно N/r »100. Что касается условия по количеству точек N = 2r, то оно рассматривается в варианте Nk £ 2r, где r - минимальное целое, а массивы с Nk < 2r дополняется до 2r нулями. В настоящее время существуют и алгоритмы БПФ с другими основаниями и их комбинациями, при которых не требуется дополнения сигналов нулями до 2r.
|
Рис. 6.1.5. Пример БПФ. |
Заметим, что в соответствии с (6.1.7) отсчеты, сопряженные с правой половиной главного частотного диапазона (0, p), относятся не к диапазону (-p,0), а к диапазону (p,2p), что, учитывая периодичность спектра дискретных данных, значения не имеет. Т.е. выходной частотный диапазон БПФ равен (0, 2p). Общее количество отсчетов комплексного спектра в этом условно главном диапазоне равно количеству точек исходного сигнала. Алгоритм быстрого обратного преобразования тождественен алгоритму прямого БПФ.
Алгоритмы прямого и обратного БПФ широко используются в современном программном обеспечении для анализа и обработки цифровых данных.
6.2. Преобразование Лапласа.
Дискретное преобразование Лапласа (ДПЛ), как и ДПФ, может быть получено из интегрального преобразования дискретизаций аргументов (tk = kDt, wn = nDw):
Y(s) = y(t)exp(-st) dt, Y(sn) = Dt
y(t)exp(-st) dt, Y(sn) = Dt y(tk)exp(-sntk), (6.2.1)
y(tk)exp(-sntk), (6.2.1)
где s = s+jw - комплексная частота, s ³ 0.
y(t) =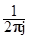
 Y(s)exp(st) ds. y(tk) = Ds
Y(s)exp(st) ds. y(tk) = Ds Y(sn)exp(sntk). (6.2.2)
Y(sn)exp(sntk). (6.2.2)
Функцию Y(s) называют изображением Лапласа функции y(t) - оригинала изображения. Нетрудно заметить, что при s = 0 преобразование Лапласа превращается в одностороннее преобразование Фурье, а для каузальных сигналов - в полную аналогию ПФ. Наиболее существенной особенностью преобразования Лапласа является возможность его применения для спектрального анализа функций, не имеющих фурье-образов из-за расходимости интегралов Фурье. Для понимания последнего запишем интеграл Лапласа в развернутой форме:
Y(s) = y(t)exp(-st-jwt) dt =
y(t)exp(-st-jwt) dt = y(t)exp(-st)exp(-jwt) dt =
y(t)exp(-st)exp(-jwt) dt = y'(t)exp(-jwt) dt.
y'(t)exp(-jwt) dt.
Правый интеграл для каузальных сигналов представляет собой преобразование Фурье, при этом сам сигнал y'(t) за счет экспоненциального множителя exp(-st) соответствующим выбором значения s>0 превращается в затухающий, конечный по энергии, что и требуется для существования его фурье-образа. Все свойства и теоремы преобразований Фурье имеют соответствующие аналоги и для преобразований Лапласа.
6.3. Z - преобразование сигналов [2,13,21].
Определение преобразования. Произвольную непрерывную функцию s(t), равномерно дискретизированную и отображенную отсчетами sk = s(kDt), равно как и непосредственно дискретную функцию, можно представить в виде степенного полинома по z, последовательными коэффициентами которого являются значения sk:
sk = s(kDt) Û TZ[s(kDt)] = sk zk = S(z). (6.3.1)
sk zk = S(z). (6.3.1)
где z = s+jv = r×exp(-jj) - произвольная комплексная переменная. Полином S(z) называют z-образом или z-изображением функции s(kDt). Преобразование имеет смысл для области тех значений z, в которой ряд сходится, т.е. сумма ряда представляет собой аналитическую функцию переменной z, не имеющую полюсов и существенно особых точек.
Пример: sk = {1, 2, 0, -1, -2, -1, 0, 0}.
S(z) = 1z0+2z1+0z2-1z3-2z4-1z5+0z6+0z7 = 1+2z-z3-2z4-z5.
Впервые z-преобразование введено в употребление П.Лапласом в 1779 и повторно "открыто" В.Гуревичем в 1947 году с изменением символики на z-1. В настоящее время в технической литературе имеют место оба вида символики.
По заданному или полученному в результате анализа какой-либо системы z-полиному однозначно восстанавливается соответствующая этому полиному функция путем идентификации коэффициентов степеней при zk с k-отсчетами функции.
Пример: S(z) = 1+3z2+8z3-4z6-2z7 = 1z0+0z1+3z2+8z3+0z4+0z5-0z6-2z7.
sk = {1, 0, 3, 8, 0, 0, -4, -2}.
Смысл величины z в z-полиноме заключается в том, что она является оператором единичной задержки по координатам функции. Умножение z-образа сигнала s(k) на величину zn означает задержку сигнала на n интервалов: znS(z) Û s(k-n).
Z-образы с положительными степенями z соответствуют каузальным (физически реализуемым) процессам и системам, которые работают в реальном масштабе времени с текущими и "прошлыми" значениями сигналов. При обработке информации на ЭВМ каузальность сигналов не относится к числу ограничений и возможно использование отрицательных степеней z, соответствующих отсчетам сигналов "вперед". Последнее применяется, например, при синтезе симметричных операторов фильтров, что позволяет производить обработку информации без внесения в сигнал фазовых искажений.
Основное достоинство z-преобразований заключается в простоте математических операций со степенными полиномами, что имеет немаловажное значение при расчетах цифровых фильтров и спектральном анализе.
Связь с преобразованиями Фурье и Лапласа. Запишем дискретный сигнал sk в виде суммы весовых импульсов Кронекера:
sk = s(kDt) = s(nDt) d(kDt-nDt).
s(nDt) d(kDt-nDt).
Определим спектр сигнала по теореме запаздывания:
S(w) = s(kDt) exp(-jwkDt).
s(kDt) exp(-jwkDt).
Выполним замену переменных, z = exp(-jwDt), и получим:
S(w) = s(kDt)×zk = S(z).
s(kDt)×zk = S(z).
Отсюда следует, что дискретное преобразование Фурье является частным случаем z-преобразования при z = exp(-jwDt).
Аналогичной подстановкой z = exp(-s) может осуществляться переход к дискретному преобразованию Лапласа.
Свойства z-преобразования. Без углубления в теорию можно констатировать, что все свойства ДПФ действительны и для z-преобразования. Особо отметим некоторые из них.
Z-преобразование линейно: Ax(kDt)+By(kDt) Û AX(z)+BY(z). Соответственно, z-преобразование допустимо только для анализа линейных систем и сигналов, удовлетворяющих принципу суперпозиции.
Для z-преобразования действительны все известные теоремы о спектрах. В частности, свертка двух сигналов отображается в z-области произведением их z-образов, и наоборот:
s(kDt) * h(kDt) Û S(z)H(z), s(kDt)h(kDt) Û S(z) * H(z).
При z = exp(-jwDt) z-преобразование представляет собой особую форму представления дискретных сигналов, при которой на полином S(z) можно ссылаться как на временную функцию (по значениям коэффициентов полинома), так и на функцию частотного спектра сигнала (значения S(z) по аргументу w).
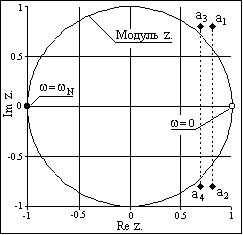
|
Рис. 6.3.1. Комплексная z-плоскость |
Отображение z-преобразования проводят на комплексной z-плоскости с Re z и Im z по осям координат (рис. 6.3.1). Спектральной оси частот w на z-плоскости соответствует окружность радиуса:
|z| = |exp(-jwDt)| = = 1.
= 1.
Подстановка значения какой-либо частоты w в z = exp(-jwDt) отображается точкой на окружности. Частоте w = 0 соответствует точка Re z = 1 и Im z = 0 на правой стороне оси абсцисс. При повышении частоты точка смещается по окружности против часовой стрелки и занимает крайнее левое положение на частоте Найквиста wN = p/Dt (Re z = -1, Im z = 0). Отрицательные частоты спектра отображаются аналогично по часовой стрелке на нижней полуокружности. Точки  wN совпадают, а при дальнейшем повышении или понижении частоты значения начинают повторяться в полном соответствии с периодичностью спектра дискретной функции. Проход по полной окружности соответствует одному периоду спектра, а любая гармоника спектра сигнала задается на плоскости двумя точками, симметричными относительно оси абсцисс.
wN совпадают, а при дальнейшем повышении или понижении частоты значения начинают повторяться в полном соответствии с периодичностью спектра дискретной функции. Проход по полной окружности соответствует одному периоду спектра, а любая гармоника спектра сигнала задается на плоскости двумя точками, симметричными относительно оси абсцисс.
Z-преобразование позволяет производить разложение сигналов и функций, например передаточных функций фильтров, на короткие составляющие операции свертки, для чего достаточно приравнять z-полином к нулю, найти его корни ai, и переписать полином в виде произведения двучленов:
S(z) = a0(z-a1)(z-a2)...,
где а0- последний отсчет сигнала (коэффициент при старшей степени z).
Но произведению в z-области соответствует свертка в координатной области и при обратном преобразовании двучлены (z-ai) превращаются в двухточечные диполи {-ai,1}, а сигнал длиной N представляется сверткой (N-1) диполей:
sk= a0{-a1,1}*{-a2,1}*{-a3,1}* ...
Пример. sk = {1.4464, -2.32, 3.37, -3, 1}. S(z) = z4-3z3+3.37z2-2.32z+1.4464. a0 = 1.
Корни полинома S(z): a1 = 0.8+0.8j, a2 = 0.8-0.8j, a3 = 0.7+0.8j, a4 = 0.7-0.8j,
S(z) = (z-0.8-0.8j)(z-0.8+0.8j)(z-0.7-0.8j)(z-0.7+0.8j).
Корни полинома представлены на z-плоскости на рис. 6.3.1. Корни полинома комплексные и четыре двучлена в координатной области также будут комплексными. Но они являются сопряженными и для получения вещественных функций следует перемножить сопряженные двучлены и получить биквадратные блоки: S(z) = (z2-1.4z+1.13)(z2-1.6z+1.28).
При переходе в координатную область: sk = {1.13, -1.4, 1) * {1.28, -1.6, 1}.
Таким образом, исходный сигнал разложен на свертку двух трехчленных сигналов (функций).
Аналитическая форма z-образов существует для z-преобразований, если возможно свертывание степенного ряда в аналитическое выражение. Так, например, для единичной (ступенчатой) функции:
u(kDt-nDt), u = 1 при k ³ n, u = 0 при k < n.
U(z) =  zk = zn(1+z+z2+z3...). U(z) = zn/(1-z), |z|<1.
zk = zn(1+z+z2+z3...). U(z) = zn/(1-z), |z|<1.
| s(k) | S(z) |
| d(k-n) u(k-n) an n nan exp(-jwnDt) | zn zn/(1-z) 1/(1-az), |a|<1 z/(1-z)2. z/(1-az)2 1/(1-z exp(-jwDt)) |
Слева в таблице приводятся аналитические формы z-преобразования функций, часто используемых на практике.
Обратное z-преобразование в общем случае производится интегрированием по контуру C, окружающему все особые точки (нули и полюсы) z-образа:
sk = (1/2pj) 
Способом, удобным для практического применения, является разложение рациональных S(z) на простые дроби. С учетом линейности преобразования:
S(z) = an/(1-bnz) Û
an/(1-bnz) Û an(bn)k = sk.
an(bn)k = sk.
Пример. S(z) = 1/(1-5z+6z2) = 3/(1-3z)-3/(1-2z) Û 3×3k -3×2k = s(k).
При разложении функции S(z) по степеням z обратное z-преобразование не вызывает затруднений.
6.4. Дискретная конволюция (свертка) [5,17,21].
Уравнение дискретной свертки двух функций (сигналов) может быть получено непосредственно из интегрального уравнения свертки при замене интегрирования суммированием мгновенных значений функций с шагом Dt:
y(kDt) = Dt s(nDt)h(kDt-nDt) = Dt
s(nDt)h(kDt-nDt) = Dt h(nDt)s(kDt-nDt). (6.4.1)
h(nDt)s(kDt-nDt). (6.4.1)
При выполнении дискретной свертки мы имеем дело с цифровыми массивами, при этом шаг дискретизации для массивов по физическому аргументу свертки должен быть равным и принимается за 1, а в качестве аргумента используется нумерация отсчетов в массивах:
y(k) = h(n)s(k-n) º
h(n)s(k-n) º  hnsk-n º yk. (6.4.1')
hnsk-n º yk. (6.4.1')
y(k) = h(n) * s(k-n) º s(k) * h(n) º sk * hn.
|
Рис. 6.4.1. Техника дискретной свертки. |
Техника свертки приведена на рис. 6.4.1. Для вычисления свертки массив одной из функций (sk- входного сигнала) располагается по ходу возрастания номеров. Массив второй функции (hn - более короткой, оператор свертки), строится параллельно первому массиву в обратном порядке (по ходу уменьшения номеров, в режиме обратного времени). Для вычисления yk значение h0 располагается против sk, все значения sk-n перемножаются с расположенными против них значениями hn и суммируются. Результаты суммирования являются выходным значением функции yk, после чего оператор hn сдвигается на один номер k вперед (или функция sk сдвигается ему навстречу) и вычисление повторяется для номера k+1 и т.д.
В начальный момент свертки при вычислении значений yk оператор hn, построенный в режиме обратного времени, "зависает" для значений k-n при n>k против отсутствующих отсчетов входной функции. "Зависание" исключают либо заданием начальных условий - дополнительных отсчетов, чаще всего нулевых или равных первому отсчету входной функции, либо началом свертки с отсчета входной функции k = n с соответствующим сокращением интервала выходной функции. Для операторов со значениями -n (вперед по времени) такой же момент может наступать и в конце входного массива.
Пример.
Уравнение свертки: yk= bnxk-n=boxk+b1xk-1+b2xk-2. Значения оператора bn: bo = 5, b1 = 3, b2 = 2.
bnxk-n=boxk+b1xk-1+b2xk-2. Значения оператора bn: bo = 5, b1 = 3, b2 = 2.
Входной сигнал: xk = {0,1,0,0,0}, начальные условия: x-i = 0.
Расчет выходного сигнала:
yo = 5xo + 3x-1+ 2x-2 = 5 x 0 + 3 x 0 + 2 x 0 = 0 y1 = 5x1 + 3xo + 2x-1 = 5 x 1 + 3 x 0 + 2 x 0 = 5
y2 = 5x2 + 3x1 + 2xo = 5 x 0 + 3 x 1 + 2 x 0 = 3 y3 = 5x3 + 3x2 + 2x1 = 5 x 0 + 3 x 0 + 2 x 1 = 2
y4 = 5x4 + 3x3 + 2x2 = 5 x 0 + 3 x 0 + 2 x 0 = 0 y5 = 5x5 + 3x4 + 2x3 = 5 x 0 + 3 x 0 + 2 x 0 = 0
Выходной сигнал: yk = {0, 5, 3, 2, 0}
Заметим: свертка функции оператора с единичным входным сигналом представляет собой повторение функции оператора свертки на выходе.
Для дискретной свертки действительны все свойства и теоремы интегральной свертки. В частности, свертка функций в координатной области отображается произведением их спектров в частотной области, что позволяет использовать ДПФ для вычисления свертки при большой длине функций по следующей схеме:
s(k) Û S(k), h(n) Û H(n), Y(k) = S(k)×H(n), Y(k) Û y(k).
Выполнение произведения спектров может производиться только при одинаковой их длине и оператор h перед ДПФ обычно дополняется нулями до размера функции s(k).
Второй фактор, который следует принимать во внимание, это цикличность свертки при ее выполнении в спектральной области, обусловленная периодизацией дискретных функций. Перемножаемые спектры являются спектрами периодических функций и результат на концевых интервалах может не совпадать с дискретной линейной сверткой, где условия продления интервалов (начальные условия) задаются, а не повторяют главный период.
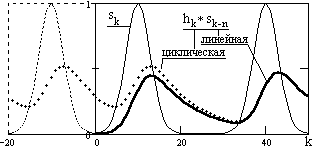
|
Рис. 6.4.2. Результаты двух видов свертки. |
На рис. 6.4.2 приведены результаты свертки сигнала sk, заданного на интервале k={0-50}, с функцией hn = a×exp(-a×n), a=0.1. Свертка, выполненная через ДПФ, в левой части интервала резко отличается от линейной свертки. Характер искажения становится понятным, если дополнить главный интервал с левой стороны его периодическим продолжением (на рисунке показана часть левого бокового периода, свертка с которым заходит в главный период). Для операторов hn со значениями n, вперед по положению, аналогичные искажения появятся и в правой части главного периода. Для устранения таких искажений функции должны продлеваться нулями на размер оператора h, что исключит наложение боковых периодов главной трассы функции.
При выполнении свертки через БПФ ощутимое повышение скорости вычислений появляется только при большой длине функций и операторов (например, M>1000, N>100). Следует также обращать внимание на разрядность результатов, т.к. перемножение чисел дает увеличение разрядности в 2 раза. При ограниченной разрядности числового представления с соответствующим округлением это может приводить к погрешностям суммирования.
Обратите внимание на лекцию "15 Сущность электрического торможения".
6.5. Дискретные функции корреляции и спектры мощности [2,17,21].
ФАК и ФВК случайных дискретных последовательностей s(k) и q(k), образованных равномерно распределенными по координате отсчетами, оцениваются по формулам:
Rs,N(n) (1/N)
(1/N) s(k)s(k+n), (6.5.1)
s(k)s(k+n), (6.5.1)
Rsq,N(n) (1/N)
(1/N) s(k)q(k+n), (6.5.2)
s(k)q(k+n), (6.5.2)
где N-интервал корреляции. Под значениями функций s и q здесь и в дальнейшем без дополнительных индексов будем понимать их центрированные значения.
Погрешность оценки корреляционных функций растет по мере увеличения сдвига (аргумента n). Усечение ФАК до значения N означает умножение ФАК на прямоугольную весовую функцию ПN(k), что в частотной области отображается сверткой спектра мощности с функцией отсчетов sinc(pfN). Как правило, спектры мощности случайных функций являются весьма изрезанными и определенная степень сглаживания, которая происходит при свертке, улучшает оценку спектра мощности. Но прямоугольная весовая функция на резких скачках спектра может вызывать явление Гиббса и появление даже отрицательных значений мощности, поэтому при усечениях ФАК рекомендуется использовать весовые функции, не имеющие в своих спектрах больших осцилляций, особенно с отрицательными значениями (весовые функции Карре, Лапласа, Кайзера или треугольное весовое окно).