Дискретизация сигналов
Тема 5: дискретизация сигналов
Все вещи таковы, каков дух того, кто ими владеет. Если он умеет ими пользоваться, они хороши. Если не умеет - плохи.
Публий Теренций. Сам себя наказующий.
Римский драматург, II в.до н.э.
Дискретизация, это очень сложно, если не знать теории. Студентом не раз пытался равномерно дискретизировать палку ливерной колбасы. Никогда не получалось. Свой кусок всегда был на рубль длиннее и на полтинник толще.
Александр Кудрявцев. Сам себя ублажающий.
Уральский геофизик и конструктор, XX в.
Содержание: 5.1. Задачи дискретизации сигнальных функций. Принципы дискретизации. Воспроизведение сигнала. 5.2. Равномерная дискретизация. Спектр дискретного сигнала. Интерполяционный ряд Котельникова-Шеннона. Дискретизация с усреднением. Дискретизация спектров. Информационная тождественность динамической и спектральной формы сигнала. Дискретизация усеченных сигналов. Соотношение спектров одиночного и периодического сигналов. 5.3. Дискретизация по критерию наибольшего отклонения. 5.4. Адаптивная дискретизация. 5.5. Квантование сигналов. 5.6. Децимация и интерполяция данных. Литература.
5.1. Задачи дискретизации сигнальных функций [10, 21].
Рекомендуемые материалы
В первой половине ХХ века при регистрации и обработке информации использовались, в основном, измерительные приборы и устройства аналогового типа, работающие в реальном масштабе времени, при этом даже для величин, дискретных в силу своей природы, применялось преобразование дискретных сигналов в аналоговую форму. Положение изменилось с широким распространением микропроцессорной техники и ЭВМ. Цифровая регистрация и обработка информации оказалась более совершенной и точной, более универсальной, многофункциональной и гибкой. Мощь и простота цифровой обработки сигналов настолько преобладают над аналоговой, что преобразование аналоговых по природе сигналов в цифровую форму давно стало производственным стандартом.
Под дискретизацией сигналов понимают преобразование функций непрерывных переменных в функции дискретных переменных, по которым исходные непрерывные функции могут быть восстановлены с заданной точностью. Роль отсчетов выполняют квантованные значения функций в дискретной шкале координат. Под квантованием понимают преобразование непрерывной по значениям величины в величину с дискретной шкалой значений из конечного множества разрешенных, которые называют уровнями квантования. Если уровни квантования нумерованы, то результатом преобразования является число, которое может быть выражено в любой числовой системе.
Для производственных задач обработки данных обычно требуется значительно меньше информации, чем ее поступает от измерительных датчиков в виде непрерывного аналогового сигнала. При статистических флюктуациях измеряемых величин и конечной погрешности средств измерений информация о величине сигнала всегда ограничена. Рациональное выполнение дискретизации и квантования исходных данных дает возможность снизить затраты на хранение и обработку информации. Использование дискретных сигналов позволяет применять методы кодирования информации с возможностью последующего обнаружения и исправления ошибок при обращении информации. Цифровая форма сигналов облегчает также унификацию операций преобразования информации на всех этапах ее обращения.
Принципы дискретизации. Представление сигнала s(t) на интервале Т совокупностью дискретных значений сi записывается в виде:
(с1,с2,...,сN) = А[s(t)],
где А - оператор дискретизации. Запись операции восстановления сигнала s(t):
s'(t) = В[(с1,с2,...,сN)].
Выбор операторов А и В определяется требуемой точностью восстановления сигнала. Наиболее простыми являются линейные операторы. В общем случае:
сn = qn(t)s(t) dt, (5.1.1)
qn(t)s(t) dt, (5.1.1)
где qn(t) - система весовых функций. Воспроизводящая функция s'(t) соответственно представляется аппроксимирующим полиномом:
s'(t) = сnvn(t), (5.1.2)
сnvn(t), (5.1.2)
где vn(t) - система базисных функций. Базисные функции ортогональны и обеспечивают сходимость ряда к s(t) при n Þ ¥. Оптимальными являются методы дискретизации, обеспечивающие минимальный числовой ряд при заданной погрешности воспроизведения сигнала.
Отсчеты в выражении (5.1.1) связаны с операцией интегрирования, что обеспечивает высокую помехоустойчивость дискретизации. Однако в силу сложности технической реализации "взвешенного" интегрирования, последнее используется достаточно редко, при высоких уровнях помех. Так, в принципе, прямое и обратное преобразование Фурье может рассматриваться как один из способов дискретизации и восстановления аналоговых данных. Более широкое распространение получили методы, при которых сигнал s(t) заменяется совокупностью его мгновенных значений s(tn), т.е. отсчетов в моменты времени tn. Роль весовых функций в этом случае выполняют импульсы Кронекера. Отрезок времени Dt между соседними отсчетами называют шагом дискретизации. Дискретизация называется равномерной с частотой F=1/Dt, если значение Dt постоянно по всему диапазону преобразования сигнала. При неравномерной дискретизации значение Dt между выборками может изменяться по определенной программе или в зависимости от изменения каких-либо параметров сигнала.
Воспроизведение сигнала по выборкам может проводиться как на основе ортогональных, так и неортогональных базисных функций. При неортогональных базисных функциях используются, в основном, степенные алгебраические полиномы вида:
s'(t) = cntn. (5.1.3)
cntn. (5.1.3)
Если значения аппроксимирующего полинома совпадают со значениями выборок в моменты их отсчета, то такой полином называют интерполирующим. В качестве интерполирующих полиномов обычно используются многочлены Лагранжа. Для реализации интерполирующих полиномов необходима задержка сигнала на интервал дискретизации, что в системах реального времени требует определенных технических решений. В качестве экстраполирующих полиномов используют, как правило, многочлены Тейлора.
Естественным требованием к выбору частоты дискретизации является внесение минимальных искажений в динамику изменения сигнальных функций. Логично полагать, что искажения информации будут тем меньше, чем выше частота дискретизации F. С другой стороны также очевидно, что чем больше значение F, тем большим количеством цифровых данных будут отображаться сигналы и большее время будет затрачиваться на их обработку. В оптимальном варианте значение частоты дискретизации сигнала F должно быть необходимым и достаточным для обработки информационного сигнала с заданной точностью
5.2. Равномерная дискретизация [16,21].
Спектр дискретного сигнала. Допустим, что для обработки задается произвольный аналоговый сигнал s(t), имеющий фурье-образ S(f). Равномерная дискретизация непрерывного сигнала s(t) с частотой F (шаг Dt = 1/F = q) с математических позиций означает умножение функции s(t) на гребневую (решетчатую) функцию Шq(t) =  d(t-kDt):
d(t-kDt):
sq(t) = s(t)×Шq(t) = s(t) d(t-kDt) =
d(t-kDt) = s(kDt)d(t-kDt). (5.2.1)
s(kDt)d(t-kDt). (5.2.1)
С учетом известного преобразования Фурье гребневой функции
Шq(t) Û F×ШF(f)
фурье-образ дискретной функции sq(t):
SF(f) = S(f) * F×ШF(f). (5.2.2)
ШF(f) = d(f-nF). (5.2.3)
d(f-nF). (5.2.3)
Отсюда, для спектра дискретного сигнала имеем:
SF(f) = F×S(f) * d(f-nF) = F
d(f-nF) = F S(f-nF). (5.2.4)
S(f-nF). (5.2.4)
|
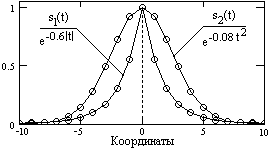
Рис. 5.2.1. Дискретные сигналы. |
Из выражения следует, что спектр дискретного сигнала представляет собой непрерывную периодическую функцию с периодом F, совпадающую с функцией F×S(f) непрерывного сигнала s(t) в пределах центрального периода от -fN до fN, где fN = 1/2Dt = F/2 - частота Найквиста. Центральный период функции SF(f) называют главным частотным диапазоном.
Как правило, шаг дискретизации сигнала (шаг числовых данных в массивах) условно принимают равным Dt = 1, при этом главный частотный диапазон занимает интервал -0.5£f£0.5, или, в шкале угловых частот, соответственно -p £ w £ p. Примеры равномерной дискретизации аналоговых сигналов s1(t) = exp(-a|t|) и s2(t) = exp(-bt2) (дискретные отсчеты нанесены кружками) и спектры этих дискретных сигналов приведены на рис. 5.2.1 и 5.2.2.
|
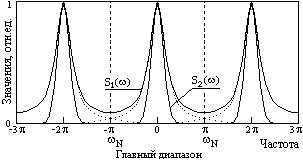
Рис. 5.2.2. Спектры дискретных сигналов (главный и 2 боковых частотных диапазона). |
Для того чтобы периодическое повторение спектра, вызванное дискретизацией аналогового сигнала, не изменяло спектр в главном частотном диапазоне (по отношению к спектру исходного аналогового сигнала), необходимо и достаточно, чтобы максимальные частотные составляющие fmax в спектре аналогового сигнала не превышали частоты Найквиста (fmax £ fN = F/2). Это означает, что частота дискретизации сигнала должна быть минимум в два раза выше максимальной частотной составляющей в спектре сигнала:
F = 1/Dt ³ 2fmax, (5.2.5)
что обеспечивает выход спектра на нулевые значения на концах главного диапазона, как это имеет место для спектра S2(w) на рис. 5.2.2.
Другими словами, на одном периоде колебаний с частотой fmax должно быть минимум две точки отсчета. Это и понятно – по одной точке отсчета на периоде гармонического сигнала определение частоты данной гармоники невозможно. На рис. 5.2.2 наглядно видно, что частота дискретизации для сигнала s1(t) данному условию не удовлетворяет и спектры периодов наложились (фактические спектры в области наложения спектра главного частотного диапазона со спектрами боковых диапазонов показаны пунктиром).
Интерполяционный ряд Котельникова-Шеннона. Умножая функцию (5.2.2) на прямоугольную весовую функцию ПF(f), равную 1 в пределах главного частотного диапазона [-F/2,F/2] и нулю за его пределами, получаем непрерывный спектр в бесконечных по частоте границах, равный спектру F×S(f) в пределах главного частотного диапазона:
F×S(f) = F×[S(f) * ШF(f)]×ПF(f). (5.2.6)
Обратное преобразование Фурье такого спектра должно давать конечный и непрерывный сигнал. Произведем обратное преобразование обеих частей равенства (5.2.6):
F×s(t) = F×sq(t) * sinc(pFt).
s(t) = sinc(pFt) * s(kDt)d(t-kDt),
s(kDt)d(t-kDt),
Отсюда, с учетом равенства d(t-kDt) * sinc(pFt) = sinc[pF(t-kDt)], получаем:
s(t) = s(kDt) sinc[pF(t-kDt)]. (5.2.7)
s(kDt) sinc[pF(t-kDt)]. (5.2.7)
Эта конечная формула носит название интерполяционного ряда Котельникова-Шеннона. По существу, ряд представляет собой разложение сигнала по системе ортогональных функций sinc(pF(t-kDt)) = sinc(p(t/Dt – k)).
Из совокупности выше приведенных формул следует, что если для частоты дискретизации сигнала справедливо неравенство F ³ 2fmax, где fmax - наибольшая частота в спектре произвольной непрерывной функции s(t), то функция s(t) без потери точности может представляться в виде числовой последовательности дискретных значений s(kDt), k = 0,1,2,..., и однозначно по этой последовательности восстанавливается. В этом и состоит сущность теоремы отсчетов Котельникова-Шеннона.
Дискретизация с усреднением. Если дискретизация сигнала производится импульсами конечной ширины, то таким импульсам соответствуют средние значения сигнала на интервале длительности импульсов. При длительности импульсов r имеем:
s(kDt) = (1/r) s(t) dt. (5.2.8)
s(t) dt. (5.2.8)
С использованием селектирующей и гребневой функций эта операция отображается следующим образом:
sq(t) = (1/r)[s(t) * Пr(t)]Шq(t). (5.2.9)
Соответственно спектр дискретизированной функции:
SF(f) = [S(f)×sinc(pfr)] * F×ШF(f). (5.2.10)
Отсюда следует, что при дискретизации с усреднением спектр S(f) заменяется спектром S(f)×sinc(pfr), периодическое продолжение которого и образует спектр дискретизированной функции. При обратном преобразовании Фурье и при использовании интерполяционной формулы Котельникова-Шеннона, вместо исходной функции s(t) получаем функцию s'(t) = s(t) * Пr(t)/r, что эквивалентно пропусканию сигнала через фильтр с откликом h(t) = Пr(t)/r, т.е. через низкочастотный сглаживающий фильтр "скользящего" среднего с окном r.
Допустим r=lDt, l£1, F=2afmax, a³1. Для этих условий частотная передаточная функция фильтра записывается в следующем виде: H(f) = sinс[(pl/2a)(f/fmax)]. Если потеря составляющих сигнала на всех частотах не должна превышать 3%, необходимо выполнить условие: sinc(pl/2a)³0,97. При a=1 отсюда следует, что значение l должно быть равно l£0.27, т.е. ширина импульса дискретизации может составлять до 27 % расстояния между импульсами.
Отметим, что в выражении (5.2.8) значения отсчетов относится к центру интервалов r импульсов дискретизации. Если отсчет будет относиться к концу интервалов r, что имеет место при обработке информации в режиме реального времени, то в выходной функции (5.2.9) появится сдвиг на интервал r/2, а в ее спектре соответственно сдвиг фаз на wr/2 (в правой части выражения (5.2.10) добавится множитель exp(-jpfr)).
Дискретизация спектров. Теоремы, доказанные для прямого преобразования Фурье, в такой же мере действительны и для обратного. При дискретизации спектра сигнала с шагом Df динамическое представление сигнала также становится периодическим с периодом Т = 1/Df. Для сохранения возможности точного восстановления сигнала в пределах главного периода (без наложения сигналов соседних периодов) частотный шаг дискретизации должен удовлетворять условию:
Df £ 1/T. (5.2.11)
Попутно отметим, что для временной формы каузального сигнала главным периодом принимают интервал от 0 до Т, хотя при обработке данных на ЭВМ это не имеет значения и главный период может устанавливаться от -Т/2 до Т/2.
Информационная тождественность динамической и частотной форм дискретного представления сигнала непосредственно следует из теоремы Котельникова-Шеннона.
Основой любых преобразований при обработке данных обычно является финитный (конечный по длительности) сигнал, зарегистрированный на интервале 0-Т и состоящий из определенных частотных составляющих от 0 до fmax. Оптимальная дискретизация аналогового сигнала без потери точности его восстановления, как рассмотрено выше, соответствует двум отсчетам на периоде максимальной частотной составляющей:
Dt = 1/2fmax, Nt = T/Dt. (5.2.12)
где Nt – общее количество отсчетов на интервале Т задания сигнала. Если сигнал зарегистрирован непосредственно в дискретной форме, то он автоматически ограничен по максимальной частоте, т.е. максимальные частоты в таком сигнале равны fmax £ 1/2Dt.
При переводе дискретного сигнала в частотную форму спектр сигнала непрерывен и периодичен с периодом 1/Dt = 2fN. Для оптимальной дискретизации по частоте без потери точности восстановления непрерывного спектра должны выполняться условия:
Df = 1/T = 1/(DtNt), fN = 1/2Dt, (5.2.13)
Nf = 2fN/Df = Nt. (5.2.14)
Спектр сигнала подвергается каким-либо преобразованиям (обработке), как правило, только в главном частотном диапазоне и тем самым превращается в непериодический сигнал, существующий только в интервале 2fN (от -fN до fN). Значения спектра за пределами главного диапазона по умолчанию полагаются равными нулю. При обратном переводе такого сигнала из частотной формы в динамическую сигнал также является непрерывным и периодическим с периодом 1/Df = T, при этом оптимальная дискретизация по координатам без потери точности восстановления непрерывной формы соответствует условиям:
Dt = 1/2fN, T = 1/Df, (5.2.15)
Nt = T/Dt = Nf. (5.2.16)
При осуществлении преобразований s(kDt) Û S(nDf), равно как и S(nDf) Û s(kDt), условие Nf = Nt является необходимым и достаточным для полного сохранения информации при преобразованиях сигнала из одной формы представления в другую. Условия (5.2.12-16) задают оптимальность преобразований без потерь информации. Если исходный сигнал дискретизирован оптимально и представлен N отсчетами, то уменьшение количества отсчетов при преобразовании неизбежно приводит к определенным потерям информации.
|
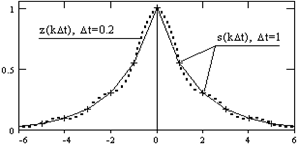
Рис. 5.2.3. |
Что касается увеличения числа отсчетов при преобразовании функций (уменьшение интервалов дискретизации), то оно всегда возможно, т.к. выходной сигнал преобразования финитных сигналов является непрерывной функцией и, в принципе, интервал дискретизации может быть установлен бесконечно малым. Однако увеличение числа отсчетов не увеличивает ни количества информации, заключенной в исходном сигнале, ни точности ее представления. По существу, такая операция полностью эквивалентна интерполяции исходного сигнала рядом Котельникова-Шеннона. Пример такой операции приведен на рис. 5.2.3.
Отсчеты s(kDt) и огибающая их кривая на рисунке 5.2.3 повторяют (в более детальном масштабе) сигнал s1(t) на рис. 5.2.1, дискретизированный с шагом Dt = 1. Как уже отмечалось, интервал дискретизации данного сигнала оказался завышенным, и спектр сигнала искажен (рис. 5.2.2). При выполнении операции s(kDt) Þ S(nDf) количество точек дискретизации спектра S(nDf) было увеличено в 5 раз по отношению к количеству точек сигнала s(kDt), т.е. Nf = 5Nt. При обратном преобразовании S(nDf) Þ z(kDt), были выполнены условия (5.2.15-16), при этом шаг дискретизации сигнала при его восстановлении оказался также в 5 раз меньше исходного (Dt = 0.2). Результат можно видеть на рис. 5.2.3 (кривая z(kDt)). Абсолютно такой же результат дает и интерполяция сигнала s(kDt) рядом Котельникова-Шеннона с переводом на шаг Dt = 0.2. Искажение аналогового сигнала закладывается при его дискретизации, если шаг дискретизации не удовлетворяет условию (5.2.5), и при любых дальнейших преобразованиях уже не может быть исправлено, т.к. информация о первоначальной форме аналогового сигнала при некорректной дискретизации утрачивается безвозвратно.
|
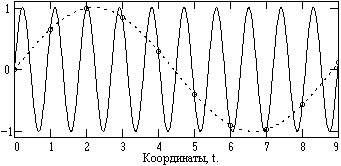
Рис. 5.2.4. Искажение сигнала при некорректной дискретизации (¾ аналоговый сигнал, o - отсчеты с шагом Dt=1, - - - "кажущийся" сигнал). |
Физическую природу искажения сигналов при некорректной дискретизации можно видеть на рис. 5.2.4. Исходный аналоговый сигнал представлен синусоидой с частотой f (непрерывная кривая) и дискретизирован с шагом Dt>1/2f. Но, и повторим это еще раз, значение какой-либо частотной составляющей в сигнале можно определить только в том случае, если на один ее период приходится не менее 2 точек дискретизации. Если это условие не выполняется, то информация по двум рядом расположенным точкам дискретизации соответствует значению "кажущейся" частоты, что и демонстрирует рис. 5.2.4. Если в дискретизируемом аналоговом сигнале присутствуют составляющие с частотами выше частоты Найквиста, то они как бы зеркально "отражаются" в главный частотный диапазон от его границ (на частоте Найквиста). Это можно видеть на рис. 5.2.2 для действительного спектра сигнала S1(w), показанного точками.
Дискретизация усеченных сигналов. Задача дискретизации усложняется для сигналов бесконечной длительности или спектров, неограниченных по частоте (последнее имеет место, если в сигнале присутствуют разрывы и резкие скачки).
Длительность сигнала и ширина его спектра не могут быть одновременно ограничены конечными интервалами. Если длительность сигнала ограничена и сигнал урезан в области его значимых (не нулевых) значений, то спектр сигнала неограничен и наоборот. Однако обработка реальных сигналов возможна только с их ограничением, как по координатам, так и по ширине спектра. При этом в качестве оценки корректности ограничения сигналов используется энергетический критерий, согласно которому длительность сигнала Т и практическую ширину спектра W устанавливают такими, чтобы в них была сосредоточена подавляющая часть энергии сигнала. Последнее достигается при выполнении условий:
 |s(t)|2 dt = k
|s(t)|2 dt = k |s(t)|2 dt, (5.2.17)
|s(t)|2 dt, (5.2.17)
 |S(w)|2 dw = k
|S(w)|2 dw = k |S(w)|2 dw, (5.2.17')
|S(w)|2 dw, (5.2.17')
где k- коэффициент качества отображения сигнала, задаваемый от 0,9 до 0,99.
Допустим, что произвольный сигнал s(t) рассматривается в пределах конечного интервала [-Т/2,Т/2] и принимается равным нулю за его пределами. Такой сигнал может быть получен умножением сигнала s(t) на прямоугольную весовую функцию ПT(t):
sT(t) = s(t)ПT(t).
Для спектра ST(f) функции sT(f) соответственно имеем:
ST(f) = S(f) * Т×sinc(pfT). (5.2.18)
Спектр ST(f) неограничен, поскольку неограничен носитель функции sinc(pfT). Отсюда следует, что частота дискретизации функции sT(t) в принципе должна быть бесконечно большой, т.е. корректная дискретизация невозможна. На практике полагают, что спектр ST(f) также определен в конечной области [-W,W]:
S'T(f) = ST(f)×П2W(f),
при этом вне этой области, по оценке Шеннона, для спектра ST(f) справедлива формула:
|ST(f)| » 1/WТ, f Ï (-W,W). (5.2.19)
Но усеченная часть спектра определяет дисперсию разности значений между исходной функцией sТ(t) и функцией s'Т(t), восстановленной по усеченному спектру S'T(f), т.к. отсеченных гармоник будет недоставать для полного восстановления функции sT(f). При выполнении условия (5.2.17'), из выражения (5.2.19) следует:
s2 £ 1/WТ, s £ 1/ . (5.2.20)
. (5.2.20)
С другой стороны, частота W при усечении спектра может рассматриваться в качестве частоты Найквиста для сигнала sT(t) при его дискретизации. При этом частота дискретизации должна быть не менее F = 2W, а количество точек дискретизации не менее N=TF=2WT.
В силу тождественности свойств прямого и обратного преобразования Фурье аналогичная методика может применяться и для оценки условий дискретизации спектров.
Таким образом, дискретизация усеченных сигналов возможна, однако при обработке усеченных сигналов необходимо проявлять осторожность и контролировать как характер возникающих искажений сигнала (определенное сглаживание спектра ST(f) относительно S(f) с возможным ухудшением разрешающей способности по частоте), так и значение средней квадратической ошибки искажений, которая, в отличие от энергетического критерия, является интегральной по пространству сигнала. Так, например, при усечении функции автокорреляции в спектре мощности сигнала могут появиться отрицательные значения, т.к. функция отсчетов sinc(pfT) в (5.2.18) является знакопеременной. Другой пример - проектирование частотных полосовых фильтров. При задании передаточной функции фильтра H(f) в частотной области в виде П-образной функции H(f) = Пr(f) обратное преобразование Фурье дает импульсный отклик фильтра h(t) Û H(f) бесконечно большой длины. Усечение отклика hT(t) = h(t)ПT(t) вызывает изменение передаточной функции фильтра (явление Гиббса): HT(f) = Пr(f) * ПT(f) Þ Пr(f)×Т× sinc(pfT), при этом по краям границ между полосой пропускания и подавления сигнала появляются затухающие флюктуации с амплитудой первого выброса до 9% от значений коэффициента передачи фильтра в полосе пропускания.
Так как частотный характер искажений, возникающих при усечении сигнала, определяется весовой функцией ПT(t) Û Т×sinc(pfT), то допустимый уровень и форму искажения сигнала можно устанавливать не только подбором интервала Т, но и применением других весовых функций. Так, для исключения появления отрицательных значений в спектрах мощности усечение функций автокорреляции целесообразно выполнять весовыми функциями, которые не имеют отрицательных значений в своих спектрах. Одной из таких функций является, например, треугольная весовая функция (окно Бартлетта).
Отметим также, что дискретизируемые сигналы, как правило, содержат широкополосные шумы, высокочастотные составляющие которых неизбежно перекрываются при периодизации спектра и увеличивают погрешность восстановления сигналов. Для исключения этого фактора перед проведением дискретизации должно быть обеспечено подавление всех частот выше fmax сигнала, т.е. выполнена низкочастотная фильтрация сигнала. Если последнее не проведено, то при дискретизации целесообразно в 3-5 раза уменьшить интервал дискретизации относительно оптимального и первой операцией обработки выполнить низкочастотную цифровую фильтрацию сигналов, после чего можно провести децимацию данных.
Соотношение спектров одиночного и периодического сигналов. Спектр ST(f) = S(kDf) периодического сигнала sT(t) с периодом Т дискретен (Df = 1/T). Спектр S(f) одиночного сигнала s(t), заданного на интервале Т, непрерывен и представляет собой спектральную плотность сигнала при T Þ ¥. Но периодический сигнал можно представить и в виде свертки одного периода с гребневой функцией Дирака:
sT(t) = s(t) * ШT(t).
При переходе в частотную область получаем:
ST(f) = (1/T)×S(f)×Ш1/T(f) = S(kDf),
ST(f) = (1/T) S(f)d(f-k/T). (5.2.21)
S(f)d(f-k/T). (5.2.21)
Отсюда следует, что спектр периодического сигнала представляет собой дискретизированный спектр одиночного сигнала, нормированный на длительность периода.
С другой стороны, одиночный сигнал s(t) может быть получен из периодического сигнала sT(t) умножением на селектирующий прямоугольный импульс ПT(t):
s(t) = sT(t)×ПT(t).
Спектр одиночного сигнала:
S(f) = T×ST(f) * ПT(f) = Т S(kDf)×sinc[pT(f-k/T)], (5.2.22)
S(kDf)×sinc[pT(f-k/T)], (5.2.22)
т.е. непрерывный спектр одиночного сигнала однозначно устанавливается по спектру периодического сигнала (интерполяция рядом Котельникова-Шеннона в частотной области).
5.3. Дискретизация по критерию наибольшего отклонения [10].
Дискретизация по критерию наибольшего отклонения применяется, в основном, при регистрации, передаче сигналов по каналам связи и при подготовке информации к длительному хранению. Основной целью во всех этих случаях является сокращение физического объема информации.
В процессе дискретизации по критерию наибольшего отклонения задается допустимое значение погрешности восстановления сигнала s. Задача обеспечения минимальной погрешности восстановления сигнала не ставится. При восстановлении сигнала непрерывная функция s(t) аппроксимируется многочленом n-й степени. Погрешность восстановления функции s(t) многочленом sa(t) определяется остаточным членом L(t):
L(t) = s(t)-sa(t) = s(t).
Шаг дискретизации выбирается из условия обеспечения L(t) < s по всему интервалу определения функции s(t). При установленном значении s уменьшение числа отсчетов обеспечивается повышением степени аппроксимирующего многочлена. На практике обычно ограничиваются ступенчатой, линейной и параболической аппроксимацией многочленами соответственно нулевой, первой и второй степеней.
В качестве интерполирующих многочленов используют многочлены Лагранжа. Для многочленов Лагранжа нулевой степени значение sa(t) в момент времени t на интервале ti<t<ti+1 между двумя последовательными отсчетами функции принимается равным отсчету s(ti+1). Если восстановление сигнала s(t) проводить по двум отсчетам: sa(ti) = [s(ti+1)-s(ti)]/2, то при том же шаге дискретизации погрешность восстановления сигнала уменьшается вдвое. Но при использовании двух последовательных отсчетов лучше использовать многочлены Лагранжа первой степени, т.е. соединение двух последовательных отсчетов прямой линией, что дает еще большее уменьшение погрешности восстановления сигнала.
В качестве экстраполирующих многочленов используется многочлены Тейлора. Для многочлена Тейлора нулевой степени условия восстановления сигнала практически не отличаются от многочлена Лагранжа, за исключением направления (от текущего зарегистрированного отсчета и вперед по t). Для многочленов Тейлора более высоких степеней при восстановлении сигнала помимо отсчета s(ti) используется также соответствующие значения производных в точке отсчета. Восстановление сигнала многочленами Тейлора происходит без задержки во времени. Однако при использовании многочленов выше нулевой степени для точного восстановления сигнала по сравнению с интерполяционными методами требуется в два раза более высокая частота дискретизации.
5.4. Адаптивная дискретизация [10].
Частота равномерной дискретизации информации рассчитывается по предельным значениям частотных характеристик сигналов. Адаптивная дискретизация ориентирована на динамические характеристики сигнала, что позволяет обеспечивать его восстановление при минимальном числе выборок. В основе принципов адаптивной дискретизации лежит слежение за текущей погрешностью восстановления сигнала. Наиболее широкое применение получили алгоритмы дискретизации с адаптацией по длине интервала аппроксимации. Сущность дискретизации заключается в последовательном наращивании интервала аппроксимации с непрерывным сравнением сигнала s(t) с воспроизводящей функцией sa(t). При достижении заданного значения s наращивание интервала прекращается и производится отсчет значения s(ti), т.е. дискретизация является неравномерной. Для воспроизведения сигналов нерегулярной дискретизации обычно используются степенные алгебраические полиномы нулевой и первой степени в интерполяционном или в экстраполяционном вариантах.
Наиболее простой является техника адаптивной дискретизации с использованием многочлена нулевой степени. На момент ti начала каждого интервала аппроксимирующий полином sa(t) принимается равным s(ti), вычисляется текущая разность L(t) = s(t)-sa(t) и производится сравнение ее значения с заданным значением s. При фиксировании равенства L(t) = s производится очередной отсчет и начинается следующий интервал.
При использовании аппроксимирующего многочлена первой степени вычисляется значение sa(t) = s(ti)+s'(ti), где s'(t) - производная сигнала. Момент очередного отсчета определяется выполнением равенства s(t)-s(ti)-s'(ti) = s. Следует иметь в виду, что данный алгоритм неэффективен при наличии высокочастотных помех, к которым весьма чувствительна операция дифференцирования.
5.5. Квантование сигналов [5,21].
Дискретизация аналоговых сигналов с преобразованием в цифровую форму связана с квантованием сигналов. Сущность квантования заключается в округлении мгновенных значений входной функции s(t), в общем случае случайной, до ближайших значений si = niDs, где Ds- шаг квантования шкалы цифровых отсчетов. Квантование с постоянным шагом Ds называется равномерным. При квантовании сигналов в большом динамическом диапазоне значений шаг квантования может быть и неравномерным, например, логарифмическим, т.е. пропорциональным логарифму входного сигнала. Установленный диапазон шкалы квантования от smin до smax и шаг квантования Ds определяют число делений шкалы Ns = (smax-smin)/Ds и соответственно цифровую разрядность квантования. В результате дискретизации и квантования непрерывная функция s(t) заменяется числовой последовательностью {si} s(kDt). Погрешность округления e = s(kDt)-si(kDt) заключена в пределах -Ds/2<e<Ds/2 и называется шумом квантования. Требуемая точность квантования оценивается по влиянию возникающего шума квантования на последующую обработку сигналов.
s(kDt). Погрешность округления e = s(kDt)-si(kDt) заключена в пределах -Ds/2<e<Ds/2 и называется шумом квантования. Требуемая точность квантования оценивается по влиянию возникающего шума квантования на последующую обработку сигналов.
При достаточно малом шаге квантования любое значение в его пределах можно считать равновероятным, при этом значения e распределены по равномерному закону:
p(e) = 1/Ds, -Ds/2 £ e £ Ds/2.
Соответственно, дисперсия и среднее квадратическое значение шума квантования:
e2 = Ds2/12,  » 0.3 Ds. (5.5.1)
» 0.3 Ds. (5.5.1)
При задании уровня шума квантования с использованием выражения (5.5.1) нетрудно определить допустимое значение шага квантования.
Входной сигнал содержит, как правило, аддитивную смесь собственно сигнала s(t) и входной помехи q(t) с дисперсией соответственно sq2. Если помехи не коррелированны с сигналом, то после квантования суммарная дисперсия шумов:
s2 = sq2+e2.
На практике шаг квантования выбирают обычно таким, чтобы не происходило заметного изменения отношения сигнал/шум, т.е. e2<<sq2.
Вам также может быть полезна лекция "Контрольные вопросы и список литературы".
5.6. Децимация и интерполяция данных [4,5,17].
Децимацией (прореживанием, сокращением) цифровых данных принято называть уплотнение данных с удалением избыточной информации. Последнее имеет место, если шаг дискретизации данных был установлен излишне подробным и fN = 1/2Dt >> fmax сигнала. Информация высокочастотной части сигнала может быть ненужной, если основная энергия полезной части сигнала заключена в низкочастотной области. Децимация может потребоваться и в том случае, если массивы данных представлены с разным шагом дискретизации.
Децимации должна предшествовать низкочастотная фильтрация данных. Это связано с тем, что в процессе децимации шаг дискретизации Dt заменяется на новый шаг Dt' = pDt, где p>1, с соответствующим сжатием главного частотного диапазона, при этом появляется опасность отражения отбрасываемых частотных составляющих и высокочастотных шумов в главный диапазон (как и при неправильном выборе шага дискретизации). Точка отсечки низкочастотного фильтра устанавливается по новой частоте Найквиста: fN'=1/(2pDt).
Значение коэффициента р при децимации может быть произвольным, но, как правило, используются целочисленные значения и децимация выливается в простое прореживание данных. При нецелочисленном значении р децимация может проводиться с использованием интерполяционного ряда Котельникова-Шеннона (равно как и любого другого интерполяционного многочлена) или преобразования Фурье. Последнее выполняется путем перевода сигнала в частотную форму и возвращением в координатную форму с новым шагом Dt' = pDt, при этом низкочастотная фильтрация может производиться непосредственно в частотном диапазоне. Возможно также и прямое усечение главного частотного диапазона с N точек до N' = N/p с возвратом из нового частотного диапазона в координатную форму с количеством точек N', но при этом следует учитывать последствия усечения спектральной функции (умножения на прямоугольное селектирующее окно) на форму восстанавливаемого по ней сигнала (свертка исходного сигнала с фурье-образом прямоугольного селектирующего окна).
Интерполяция данных отличается от децимации только значением коэффициента р<1, с соответствующим увеличением частоты Найквиста, и не требует низкочастотной фильтрации.
Для децимации и интерполяции данных разработаны также специальные высокоскоростные методы и алгоритмы (цифровые фильтры) - экспандеры и компрессоры /4,5/.