Узкополосные сигналы

5. Узкополосные сигналы

5.1 Комплексная огибающая

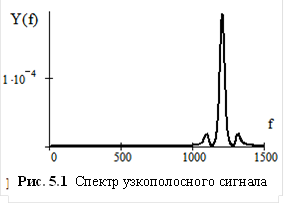
В измерительных информационных системах и в различных системах передачи информации часто используются сигналы, спектр которых сосредоточен в узком диапазоне частот , ширина которого  намного меньше среднего значения частоты  (рис. 5.1). Сигнал, спектр которого соответствует рис. 5.1, расположен в полосе частот примерно от 1000 до 1400 Гц. Полоса частот, занимаемая сигналом, равна 400 Гц, среднее значение частоты составляет 1200 Гц

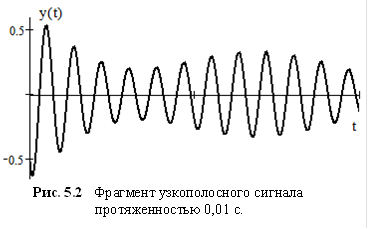
Подобные сигналы, имеющие форму почти гармонического колебания, у которого амплитуда и фаза изменяются во времени, и называются узкополосными сигналами (рис. 5.2). В каждый момент времени t значение такого сигнала x(t) можно рассматривать как значение некоторой придуманной для этого момента времени косинусоиды , амплитуда  и начальная фаза  которой различны для каждого момента времени t, а частота равна среднему значению из частотного диапазона сигнала. Такого рода узкополосный сигнал можно представить в виде выражения:

.

Переменная во времени амплитуда А(t) называется в этом случае амплитудной огибающей сигнала, начальная фаза φ(t) – фазовой функцией сигнала x(t), а весь аргумент косинуса – полной фазой сигнала:

.

Амплитудную огибающую А(t) в первом приближении можно представить себе в виде кривой, скользящей по вершинам сигнала. Фазовая функция не допускает такой простой интерпретации. По графику сигнала довольно просто восстановить форму амплитудной огибающей, но построить алгоритм выполнения этой процедуры достаточно сложно. В дальнейшем нашей задачей и будет построение алгоритма определения амплитудной огибающей и фазовой функции сигнала. Практически эта операция реализуется устройствами, которые называются амплитудными демодуляторами.

Представим узкополосное колебание в виде вещественной части комплексной экспоненты:

Рекомендуемые материалы

.

В комплексном выражении, стоящем под скобками, можно выделить два принципиально различных сомножителя:

-  - это гармоническое колебание с высокой частотой , так называемое несущее колебание,

-  - относительно медленно меняющийся сомножитель, содержащий в себе информацию как об амплитудной огибающей, так и о начальной фазе.

Этот медленно изменяющийся сомножитель и называется комплексной огибающей узкополосного сигнала:

.

Сопоставить одному сигналу x(t) сразу две функции A(t) и φ(t) можно, конечно, очень многими способами. Однако искомое представление должно удовлетворять нескольким очевидным требованиям:

- для гармонического колебания искомая процедура должна дать постоянную амплитуду и постоянную начальную фазу,

- фазовая функция не должна изменяться при умножении сигнала на произвольный множитель.

Этих ограничений достаточно, чтобы построить единственную процедуру выделения амплитудной огибающей и фазовой функции. Эта процедура основывается на использовании еще одного интегрального преобразования – преобразования Гильберта.

5.2 Преобразование Гильберта

 Для выделения амплитуды и фазы произвольного узкополосного сигнала x(t) вводится понятие аналитического сигнала

,

вещественная часть которого совпадает и исходным сигналом, а мнимая часть называется сопряженным сигналом или квадратурным дополнением.

Этот сопряженный сигнал получается из исходного сигнала x(t) с помощью преобразования Гильберта:

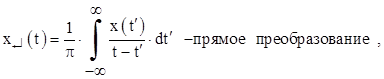
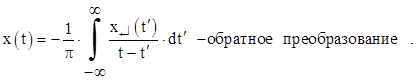
При внимательном анализе этих формул можно увидеть, что сопряженный сигнал, определяемый прямым преобразованием Гильберта, представляет собой свертку исходного узкополосного сигнала x(t) и функции 1/πt:

.

Поэтому спектральная функция сопряженного сигнала должна равняться произведению спектральной функции X(ω) сигнала x(t) и спектральной функции . Эта последняя носит название частотной характеристики преобразования Гильберта:

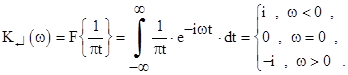
Произведение  является спектральной функцией сопряженного сигнала. Из определения частотной характеристики преобразования Гильберта следует, что спектр сопряженного сигнала отличается от спектра исходного сигнала следующими особенностями:

o из исходного сигнала удаляется постоянная составляющая,

o фазы всех спектральных составляющих в области отрицательных частот уменьшаются на π/2,

o фазы всех спектральных составляющих в области положительных частот увеличиваются на +π/2,

o амплитудные соотношения остаются без изменения.

Спектральная функция аналитического сигнала составляет:

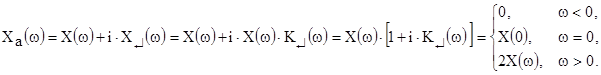
Для узкополосного сигнала, спектр которого расположен в области высоких частот, X(0)=0. Спектр аналитического сигнала оказывается односторонним. В области отрицательных частот он исчезает, а в области положительных частот увеличивается вдвое.

5.3 Построение амплитудной огибающей

Получив аналитический сигнал путем добавления к исходному сигналу мнимой части в виде сопряженного сигнала, можно вычислить:

- амплитудную огибающую как модуль комплексного аналитического сигнала

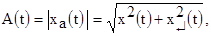
- полную фазу колебания как аргумент комплексного аналитического сигнала

.

Для того, чтобы выделить отсюда фазовую функцию, необходимо выбрать некоторое значение центрально частоты . Выбор центральной частоты, вообще то, произволен. Но, как мы увидим в дальнейшем, в каждом конкретном случае существуют разумные доводы в пользу однозначного выбора.

После выбора центральной частоты можно получить фазовую функцию и комплексную огибающую:

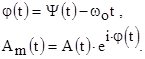
Но комплексную огибающую мы получали в результате отбрасывания из выражения для спектра исходного сигнала быстро изменяющегося во времени сомножителя . Поэтому спектр огибающей представляет собой сдвинутый на  к началу координат спектр аналитического сигнала:

.

Соотношения между спектрами сигнала, соответствующего ему аналитического сигнала и комплексной огибающей представлены на рис. 5.3.

В общем случае спектр огибающей может быть и не симметричным относительно нулевой частоты. Всегда, говоря о комплексной огибающей, необходимо указывать ту центральную частоту, относительно которой вычисляется эта комплексная огибающая.

Пример.

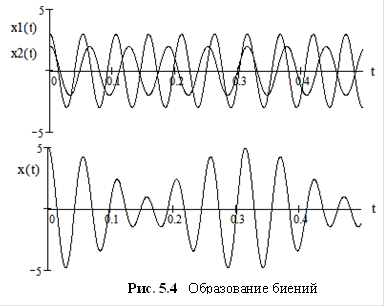
Узкополосный сигнал состоит из двух близких по частоте гармоник:

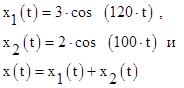
Эти сигналы представлены на рис. 5.4, исходные сигналы – в его верхней части, а итоговый сигнал – внизу.

Такого рода сигналы называются биениями. Биение – это почти гармоническое колебание с периодически изменяющейся амплитудой. На глаз легко представить себе и даже нарисовать форму огибающей. Попробуем сделать это аналитически и проверить нашу интуицию.

Сопряженный сигнал определяется преобразованием Гильберта, однако здесь можно просто использовать свойства спектра сопряженного сигнала, согласно которому все спектральные составляющие сопряженного сигнала в области положительных частот отличаются от спектральных составляющих исходного сигнала сдвигом по фазе на –π/2. Используя эти соотношения, получим:

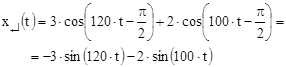
Аналитический сигнал составляет таким образом:

,

и амплитудную огибающую сигнала можно теперь вычислить как модуль этого комплексного выражения:

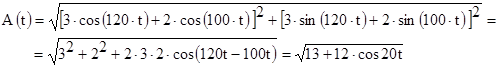
Лекция "1 Трансформаторы" также может быть Вам полезна.

Амплитудная огибающая А(t) вместе с исходным сигналом x(t) представлены на рис. 5.5.

В общем случае расчеты оказываются более сложными. Однако уже из рассмотренного примера видны основные свойства огибающей:

- всегда имеет место ,

- в моменты времени, когда , то есть когда , имеем:

,

то есть в точках касания действительного узкополосного сигнала и его амплитудной огибающей имеет место равенство и их скоростей изменения. Поэтому сигнал и его огибающая должны выглядеть именно так, как это показано на рис. 5.5.