Оценка неизвестных параметров сигнала

ГЛАВА 3.  Оценка неизвестных параметров сигнала

         Определим элементарный сеанс связи как совокупность следующих операций:

¨ выбор источником одного сообщения из множества возможных и отправление его получателю;

¨ преобразование посланного сигнала под действием помех в реализацию смеси, которая наблюдается получателем;

¨ принятие получателем по наблюдению реализации смеси решения о том, какое сообщение выбрал в данном случае источник, т.е. оценка сообщений. 

         Применение некоторого правила принятия решения (оценивания) – это установление соответствия между наблюдаемой получателем реализацией смеси и одной из возможных оценок.

         Функция двух переменных r(x_i, x_j^*), значение которой (в некотором масштабе) равно стоимости решения x_j^* при условии, что передавалось сообщение x_i , называется функцией потерь (риска, штрафа и т.д.) Если оценка ошибочна, т.е. при истинном передаваемом сообщении x_i принято решение  x_j^*≠ x_i , то неправильные действия получателя повлекут за собой некоторые потери r, которых бы не было, будь оценка безошибочной.

3.1. Байесовские оценки при различных функциях потерь

         Измерение координат и параметров сигналов является задачей статической в силу флюктуационной природы помех в смеси х(t) и в силу случайного (непредсказуемого) изменения параметров сигнала. Задачи оценки параметров сигнала и обнаружения сигнала имеют общую статистическую модель.

Рекомендуемые материалы

         Поскольку потери   r(x_i, x_j^*) в каждом элементарном сеансе случайны из-за случайности x_i, и x_j^* , построение критерия после задания функции потерь требует определения статистически устойчивого параметра, характеризующего качество системы на множестве сеансов. Чаще всего применяется подход, основанный на использовании математического ожидания потерь, при котором гарантируется минимум суммарных потерь. Математическое ожидание потерь:

                                                  (3.1)

называется средним риском, а система, минимизирующая средний риск (при условии, что функция потерь не зависит от правила решения), называется оптимальной байесовой системой.

                             (3.2)

где - совместное распределение вероятностей сообщения и оценки.

                                                                (3.3)

                                                                (3.4)

          Функцию p_z называют условным средним риском при данной реализации смеси, а р_х – условным средним риском при данном истинном сообщении. Условный средний риск при данном сообщении р_х может служить характеристикой качества системы, а условный средний риск при данной реализации смеси р_z используется для определения структуры оптимальной байесовой системы.

3.2. Неравенство Рао – Крамера

          Существует неравенство, с помощью которого можно определить нижнюю границу среднеквадратических ошибок при использовании любых оценок параметра. Предположим, что границы области действительной оси, где плотность распределения  отлична от нуля, не зависит от . Это условие выполняется, например, если на всей действительной оси и для х ≥ 0. Предположим, кроме того, что функция  дифференцируема по параметру .

          Введем новое обозначение

                                 (3.5)

чтобы подчеркнуть зависимость функции правдоподобия от неизвестного параметра .

          Неотрицательная величина

                        (3.6)

называется информацией по Фишеру о параметре , содержащейся в выборке х.

          Найдем искомую нижнюю границу дисперсии оценок (неравенство

Рао - Крамера)

                                       (3.7)

          Правая часть неравенства является также нижней границей среднеквадратических отклонений оценок от оцениваемого параметра.

          Для несмещенных оценок

                                                (3.8)

3.3. Оценки максимального правдоподобия, их свойства и связь с байесовскими

          Рассмотрим оценку векторного параметра , оптимальную по критерию максимального правдоподобия. Так как логарифм – монотонная функция, то экстремумы функций L_x() и ln L() достигаются при одинаковых аргументах . Поэтому критерий максимального правдоподобия можно представить в виде:

                                (3.9)

Функцию правдоподобия можно заменить статистикой отношения правдоподобия

                                           (3.10)

где  - фиксированный вектор.

Система уравнений максимального правдоподобия

                             (3.11)

          Оценку , удовлетворяющую системе уравнений, называют оценкой максимального правдоподобия векторного параметра   или совместной оценкой максимального правдоподобия компонента этого векторного параметра. Оценки максимального правдоподобия состоятельные и асимптотически совместно эффективные.

          Рассмотрим связь байесовых оценок с оценкой максимального правдоподобия на примере нормального распределения амплитуды сигнала.

          Байесовская оценка амплитуды а квазидетерминированного сигнала

                         (3.12)

где - оценка максимального правдоподобия,

- отношение дисперсии априорного распределения амплитуды к дисперсии ее оценки максимального правдоподобия.

          Из (3.11) следует, что байесовская оценка представляет среднее взвешенное двух величин: оценки максимального правдоподобия и априорного среднего а₀, причем отношение веса, приписываемого первой величине, к весу второй равно Ясно, что в рассматриваемом случае байесовская оценка распределенной по нормальному закону амплитуды сигнала, совпадает с оценкой максимальной апостериорной плотности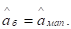

          Если отношение неограниченно возрастает, т.е. дисперсия оценки максимального правдоподобия много меньше дисперсии априорного распределения, то  ~, т.е. байесовская оценка приближается к оценке максимального правдоподобия. Если дисперсия априорного распределения много меньше дисперсии оценки максимального правдоподобия, то  ~, т.е. наблюдаемая реализация не влияет на оценку, которая принимается равной априорному среднему оцениваемого параметра.

3.4. Функционал отношения правдоподобия гауссовского процесса

          Оптимальный по любому из критериев качества аналоговый алгоритм проверки гипотезы Н₀ против альтернативы Н₁ предписывает сравнение с порогом логарифма функционала отношения правдоподобия. Поэтому для синтеза оптимального аналогового алгоритма обнаружения сигнала на фоне гауссовской помехи необходимо определить логарифм функционала отношения правдоподобия гауссовского случайного процесса с указанием ограничений, при которых этот функционал существует.

          Гипотеза Н₀ состоит в том, что наблюдаемая реализация принадлежит гауссовскому процессу с корреляционной функцией В(t,y) и средним значением s₀(t), а альтернатива Н₁ – в том, что реализация принадлежит гауссовскому процессу с той же корреляционной функцией и средним значением s₁(t). Для рассматриваемой здесь задачи обнаружения  s₀(t) ≡ 0 и s₁(t) ≡ s(t).

          Запишем логарифм отношения правдоподобия для дискретной выборки х=(х₁,…,х_n), полученной отбором на интервале (0,Т) через равные промежутки времени из реализации х(t) гауссовского случайного процесса

    (3.13)

где Х – вектор с компонентами s_1, s₀ – векторы с компонентами  - корреляционная матрица (положительно определенная) размером nxn.

Введем вектор V=K^-1(s₁-s₀).

Тогда s₁-s₀ = KV.

          После преобразований логарифм функционала отношения правдоподобия равен

                      (3.14)

где V(t) – решение интегрального уравнения:

                      (3.15)

тогда среднее значение логарифма функционала отношения правдоподобия при гипотезе и при альтернативе равен:

                                    (3.16)

где .

3.5. Оценка амплитуды детерминированного сигнала

          Рассмотрим оценку максимального правдоподобия неизвестной амплитуды а детерминированного сигнала as(t) на фоне аддитивной гауссовской помехи. Эта оценка является частным случаем оценки при m=1 и =a. Для рассматриваемого скалярного случая следует

                                          (3.17)

V(t) – решение линейного интегрального уравнения

                                       (3.18)

          Из анализа оценки максимального правдоподобия векторного параметра линейной модели сигнала следует, что оценка амплитуды сигнала несмещенная и эффективная, т.е.

   

          Доверительный интервал для неизвестной амплитуды сигнала может быть представлен неравенствами

                      (3.19)

где - процентная точка нормального распределения, определяемая по заданному коэффициенту доверия γ.

          Для реализации оптимального аналогового алгоритма оценивания амплитуды сигнала на фоне аддитивной гауссовской помехи необходимо вычислить нормированный корреляционный интеграл. Эту операцию можно осуществить при помощи аналогового коррелометра или физически реализуемого линейного фильтра с импульсной характеристикой

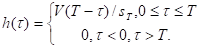
                                (3.20)

          Оптимальная оценка амплитуды получается в конце наблюдения на выходе фильтра, если только импульсная характеристика фильтра нормируется величиной s_T (или умножается на дисперсию оценки).

3.6. Оценки амплитуды и фазы гармонического сигнала

          Сигнал s(t;) – гармонический с известной частотой ω₀ и неизвестными амплитудой  а и фазой φ:

           (3.21)

                                                                          (3.22)

                                                         (3.23)

          Решая систему двух линейных относительно ₁ и ₂ уравнений, получаем оценки максимального правдоподобия этих параметров:

                            (3.24)

                              (3.25)

где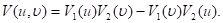

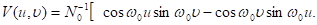
          Полагая ω₀Т = 2πk, где k – целое число, находим оценки максимального правдоподобия:

                                           (3.26)

                                           (3.27)

          Эти оценки максимального правдоподобия можно использовать для получения оценок амплитуды и фазы сигнала на фоне аддитивного белого гауссовского шума:

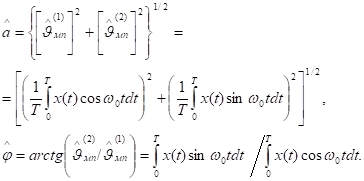
3.7. Совместная оценка частоты и фазы гармонического сигнала при аддитивном белом шуме

          Рассмотрим пример совместной оценки двух неэнергетических параметров – частоты ω и фазы φ гармонического сигнала, наблюдаемого в аддитивной смеси с белым шумом. Поскольку частота неизвестна, следует условиться, на какой момент времени приходится оценка фазы. Будем считать, что оценивается фаза, приходящаяся на середину интервала наблюдения, а наблюдение проводится, начиная с момента – Т/2 до момента Т/2.

          Уравнение, определяющее оценку частоты, запишется так:

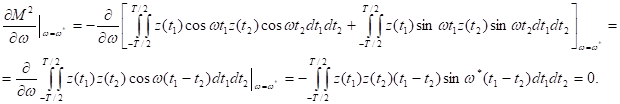
          Приведенное уравнение не имеет аналитического решения, но можно показать, что оно имеет множество корней. Воспользуемся линеаризацией этой формулы, предположив, что известно опорное значение ω, близкое к искомому решению ω^* = ω + Δω^*, причем  Δω^*Т<< π/2. Тогда, считая,  что cos Δω^*(t₁ – t₂) ≈ 1 и sin Δω^*(t₁ – t₂) ≈ Δω^*(t₁ – t₂), получаем

                        (3.28)

          Если частота находится в диапазоне шириной Ω = ω_max - ω_min, то для определения опорного значения частоты ω_i требуется число каналов

                                                                 (3.29)

3.8. Понятие об аномальных ошибках измерения

          Ошибки системы, определяющей параметры радиосигнала, обычно принято делить на два вида: малые (нормальные) и большие (аномальные). Такое разделение ошибок имеет смысл потому, что каждый из видов удобнее оценивать различными критериями. При оценке аномальных ошибок величина среднеквадратической ошибки и максимальной ошибки чаще всего не важны, ибо само появление аномальной ошибки означает нарушение работы системы, невыполнение поставленной задачи. Аномальные ошибки наиболее удобно характеризовать вероятностью их появления, и при проектировании следует создавать условия, при которых эта вероятность пренебрежимо мала.

          Если речь идет о начальном этапе проектирования, когда система еще не определена и выбирается только радиосигнал, можно считать аномальными все ошибки, лежащие вне главного экстремума функции различия ε (Δх). Область нормальных ошибок обычно располагается симметрично около нуля на оси Δх (или около х_и на оси х). Обозначим соответствующие граничные точки х_н1 и х_н2 (рис. 3.1). Эти точки лежат внутри области априорной неопределенности, границы которой обозначены х_а1 и х_а2.

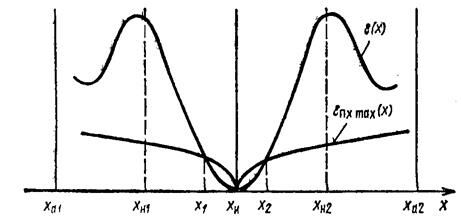
Рис. 3.1. К определению аномальных ошибок

          Допустим, что причиной является действие аддитивной помехи. Тогда, учитывая, что оценка параметра определяется наименьшим значением измеренной функцией различия, получаем достаточное условие отсутствия аномальных ошибок в виде

                                      (3.30)

          Это условие можно записать в виде

                          (3.31)

или, отбросив одинаковые члены в обеих частях неравенства, получим достаточное условие в виде

                                          (3.32)

причем это условие должно выполняться для всех х, лежащих вне области х_н1 – х_н2.

3.9. Понятие об оценке (фильтрации) меняющихся параметров сигналов

          Задача оценки сообщения сводится к задаче оценки совокупности параметров (при оценке в целом) или одного параметра (при фильтрации).

          Предположим, что на интервале наблюдения (0,Т) получена реализация х(t) аддитивной смеси сигнала ξ(t) и помехи η(t), которые представляют центрированные случайные процессы с известными корреляционными функциями В_ξ(u,υ)  и В_η(u,υ), причем и сигнал, и помеха необязательно гауссовские. Необходимо синтезировать оценку   стохастического сигнала по наблюдаемой реализации х(τ), 0≤ τ ≤ T.

          Определение оценки как функционала от х(τ) при t=T называется задачей фильтрации сигнала.

          Располагая реализацией аддитивной смеси сигнала и помехи, иногда необходимо определить также оценку некоторого стохастического сигнала , представляющего требуемую операцию над сигналом ξ(t). Это может быть линейная операция (сдвиг, однократные или многократные дифференцирование и интегрирование) или даже нелинейная.

3.10. Линейная и нелинейная фильтрация

          Линейная фильтрация. Рассмотрим задачу оптимальной линейной фильтрации сигнала на фоне аддитивной помехи, которая формируется следующим образом. В качестве оценки сигнала принимается линейный функционал

                            (3.33)

т.е. значение процесса на выходе линейного фильтра с импульсной характеристикой h(t,τ), когда на вход действует наблюдаемая реализация смеси сигнала с помехой. Необходимо в классе этих линейных фильтров определить фильтр, оптимальный по критерию минимума среднего квадрата ошибки оценивания

                            (3.34)

где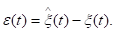

          Так как по предложению сигнал и помеха – центрированные случайные процессы, то средний квадрат ошибки совпадает с ее дисперсией. Поэтому критерий минимума среднего квадрата ошибки оценивания будем называть критерием минимума дисперсии ошибки. Для определения импульсной характеристики h^* (t,τ) такого оптимального фильтра достаточно располагать указанными априорными данными о сигнале и помехе.

          Если реализация х(τ) аддитивной смеси сигнала и помехи определена для всех действительных значений τ, тогда линейную оценку сигнала можно представить в виде

                                    (3.35)

Дисперсия ошибки оценивания

    (3.36)

         Из этой формулы видно, что дисперсия линейной оценки зависит только от корреляционных функций сигнала и помехи и не зависит от распределения вероятностей этих случайных процессов.

         Обозначим через h^* (t,τ) импульсную характеристику оптимального линейного фильтра, а через ε^*(t) ошибку оценивания сигнала при оптимальной линейной фильтрации. Тогда

 (3.37)

        

Это соотношение выражает так называемый принцип ортогонального проецирования, который является достаточным условием минимума дисперсии ошибок оценивания сигнала.

         Положительными свойствами линейных методов являются их простота по сравнению с нелинейными методами и для синтеза оптимального линейного фильтра требуются ограниченные статистические данные о сообщениях и смесях, что весьма важно с точки зрения практики.  

         Нелинейная фильтрация. Если отказаться от условия линейности алгоритма обработки наблюдаемой реализации, то в более широком классе допускаемых оценок можно получить оценки, которые по заданному критерию минимума среднего квадрата ошибки будут лучше линейных оценок. В общем случае оптимальной по критерию минимума среднего квадрата ошибки, оценкой сигнала  по наблюдаемой реализации х(τ) аддитивной смеси сигнала с помехой η(t), является условное среднее

                     (3.38)

         За исключением гауссовских процессов и η(t) вычисление нелинейного функционала встречает значительные трудности, связанные, прежде всего с определением апостериорной плотности вероятности. Один из подходов к решению задачи оптимальной нелинейной фильтрации состоит в ограничении класса исследуемых нелинейных процессов марковскими или их компонентами. При таком ограничении удается преодолеть трудности, связанные с вычислением апостериорной плотности оцениваемого процесса. После этого можно получить оценку по критерию минимума среднего квадрата ошибки. Мы рассмотрим другой подход, основанный на аппроксимации нелинейного функционала  рядом Вольтерра:

     (3.39)

         Если K_m≡0 для всех m>1, то получаем линейный функционал и K₁(u) можно трактовать как импульсную характеристику линейного фильтра. Добавление членов ряда при m>1 означает введение нелинейности. Совокупность функций K_m(u₁,…u_m), m=характеризует нелинейный фильтр n-го порядка. Ограничение  суммы ряда первыми n членами позволяет аппроксимировать функционал F[x(τ)] процессом на выходе фильтра n –го порядка при входной воздействии x(τ).

         Если n=2, то для формирования оценки использована простейшая нелинейная система – фильтр второго порядка. Задача состоит в том, чтобы определить характеристику K₂(u₁,u₂) нелинейности так, чтобы средний квадрат ошибки

                                     (3.40)

был минимальным.

         После преобразований получим минимальное значение дисперсии ошибки

 (3.41)

или

                    (3.42)

где

                          (3.43)

- минимальная дисперсия ошибки линейной оценки.

        

Таким образом, использование оптимального нелинейного корректирующего звена в фильтре второго порядка позволяет дополнительно уменьшить дисперсию ошибки на

            (3.44)

3.11. Фильтры Винера и Калмана

         Задача фильтрации (на фоне стационарного шума) сообщения, представляющего собой стационарный случайный процесс, при условии, что наблюдение длится бесконечно долго, называют обычно винеровской фильтрацией, а фильтры, структура которых находится при такой постановке задачи, называются винеровскими.

         Если и сигнал, и помеха стационарны, а фильтр представляет линейную систему с постоянными во  времени параметрами, то при t→∞ импульсная характеристика h^*(t) оптимального фильтра определяется решением интегрального уравнения

                   (3.45)

       При этом минимальное значение дисперсии ошибки

                                                                (3.46)

После преобразований следует

           (3.47)

                   Из этого условия находим передаточную функцию оптимального физически реализуемого фильтра

                           (3.48)

                   Обратным преобразованием Фурье из последней формулы находим импульсную характеристику h^*(t) оптимального физически реализуемого фильтра (решение уравнения Винера-Хопфа). Таким образом, определение оптимального физически реализуемого фильтра сводится к факторизации спектра аддитивной смеси сигнала и помехи, и разложению функции на сумму сопряженных функций. Указанная факторизация может быть всегда выполнена, если выполняется условие Винера-Пэли

                                    (3.49)

                   Фильтр Калмана. Если спектр сигнала представляет рациональную функцию переменной ω², то сигнал ξ(t) со спектром 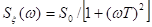получаем на выходе формирующего фильтра, структура которого определяется дифференциальным уравнением первого порядка где - белый шум со спектральной интенсивностью S_0. Предположим, что помеха η(t) также представляет белый шум с интенсивностью N₀, причем  η(t) и  некоррелированы. Используя линейную оценку сигнала, получим

                        (3.50)

Бесплатная лекция: "4.16 Внешняя политика" также доступна.

где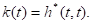

                   Выражение (3.50) представляет собой оптимальный по критерию минимума дисперсии ошибки алгоритм фильтрации сигнала со спектром на фоне аддитивного белого шума. Соответствующая этому алгоритму структурная схема оптимального фильтра (фильтра Калмана) изображена на рис. 3.2, где, кроме того, показана структурная схема формирующего фильтра, на выходе которого получаем сигнал со спектром. Здесь осталась неизвестной функция k(t), которую называют коэффициентом усиления. Она равна

                                          (3.51)

т.е. коэффициент усиления полностью определяется минимальным значением дисперсии ошибки при линейной фильтрации сигнала.

Рис. 3.2. Схема фильтра Калмана