Кинематика механизмов с низшими кинематическими парами
4. Кинематика механизмов с низшими кинематическими парами
В этом разделе изучаются методы исследования кинематики механизмов с низшими парами (или рычажных механизмов).
4.1. Задачи исследования; исходные данные; методы исследования
Задачи исследования
1)Определение положений звеньев механизма и определение траекторий отдельных его точек.
2)Определение линейных скоростей точек механизма и угловых скоростей его звеньев.
3)Определение линейных ускорений точек механизма и угловых ускорений его звеньев.
Исходные данные
Для решения задач кинематики необходимо иметь
Рекомендуемые материалы
1)Кинематическую схему механизма и все кинематические размеры его звеньев.
2)Закон движения входного (ведущего) звена.
Методы исследования
1)Аналитический.
2)Графо-аналитический (метод планов положений,скоростей и ускорений).
3)Метод графического дифференцирования.
4)Экспериментальный.
4.2.Аналитический метод
Метод заключается в определении математических выражений, 
описывающих функциональную связь между входными и выходными параметрами механизма. Для этого служат различные приёмы и методы, такие как метод векторных контуров, который образуется заменой кинематических размеров звеньев векторами, с последующим проецированием этого контура на оси системы координат и получением на этой основе соответствующих уравнений, описывающих кинематику данного механизма. Этой же цели служит метод разбиения схемы механизма на прямо- или косоугольные треугольники, решая которые, получают необходимые математические выражения.
Для составления некоторого первоначального представления о методе рассмотрим кинематику синусного механизма (рис. 4.1). Механизм состоит из кривошипа 1, вращающегося вокруг неподвижной точки О, конец А которого образует вращательную кинематическую пару с ползуном 2. Ползун движется по вертикальному элементу ведомого звена 3, которое движется вдоль неподвижных гоизонтальных направляющих. На первом этапе определяется зависимость перемещения S ведомого звена от угла α1 поворота ведущего кривошипа 1. Из рис. 4.1 видно, что
.
Дифференцируя по 
в первый раз, получаем аналог скорости ведомого звена:
,
дифференцируя во второй раз, получаем аналог ускорения ведомого звена
.
З а м е ч а н и е . Следует обратить внимание на то, что зависимость 
, отражающая закон преобразования движения в механизме, называется функцией положения механизма. Её первая производная по , как отмечено выше, называется аналогом скорости (или передаточной функцией скорости), вторая производная – аналогом ускорения (или передаточной функцией ускорения). Для получения скорости и ускорения в функцию положения необходимо ввести время, для этого вместо необходимо подставить 
и выполнить дифференцирование по времени 
. Попутно обнаруживается и связь между кинематическими функциями и их аналогами.
4.3. Метод планов положений, скоростей и ускорений
Определение функции положения
При использовании графоаналитического метода определение функции положения механизма производится с помощью разметки механизма. Разметка механизма – это ряд последовательных положений механизма, построенный в зависимости от положений входного звена, охватывающих весь цикл его движения (как правило, один оборот). Каждый механизм в соответствии с его кинематической схемой имеет свои особенности в построении разметки. Разметка строится в некотором масштабе, начиная от одного из крайних положений, отмечаемого нулевым номером. Затем окружность, описываемая концом входного звена (кривошипа), делится на двенадцать равных частей, которые обозначаются номерами в направлении угловой скорости. После этого строятся положения остальных звеньев механизма, и строятся траектории заданных точек.
Для примера на рис. 4.2 приведена разметка кривошипно – ползунного механизма, с помощью которой легко определить путём измерений перемещения точки В ведомого звена, соответствующие углам поворота кривошипа, и представить их в виде графика или таблицы. Это и будет функция положения механизма.
З а м е ч а н и е о м а с ш т а б е . Масштабом называется число, показывающее, сколько единиц физической величины содержится в одном миллиметре её изображения. В механике машин в масштабе изображаются любые физические величины: угол поворота, время, перемещение, скорость, сила, работа, мощность и т. д. Масштаб обозначается буквой 
с индексом обозначения физической величины и имеет размерность в виде дроби, в числителе которой указывается размерность изображаемой физической величины, в знаменателе – миллиметры. Например: 
– масштаб длин читается: ноль целых, две тысячных метра в одном миллиметре (изображения); 
– масштаб времени, читается: две секунды в одном миллиметре.
Определение скоростей и ускорений
Планом скоростей (ускорений) механизма называется пучок векторов, выходящих из одной точки (полюса плана), каждый из которых в некотором масштабе изображает вектор абсолютной скорости (абсолютного ускорения) какой-либо точки механизма, а отрезки, соединяющие их концы, изображают векторы относительных скоростей (относительных ускорений).
Построение плана скоростей сводится к реализации известного положения теоретической механики, согласно которому при плоско-параллельном движении твёрдого тела (звена) скорость любой его точки равна векторной сумме скорости в поступательном переносном движении вместе с другой точкой, принятой в качестве полюса, и скорости её в относительном вращательном движении относительно этого полюса.
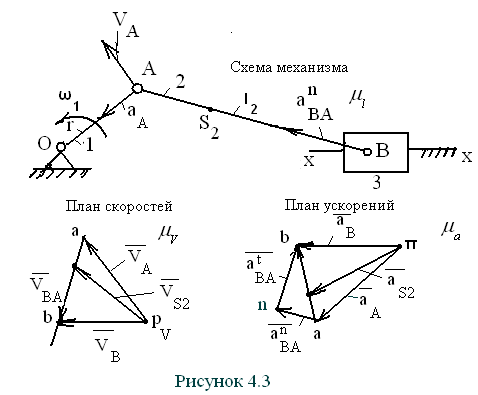
Рассмотрим построение планов скоростей и ускорений на примере кривошипно-ползунного механизма (рис. 4.3). Схема механизма должна быть изображена в масштабе 
в исследуемом положении. Прежде необходимо определить параметры движения точки А. Её скорость по величине равна произведению угловой скорости 
кривошипа 1 на его радиус 
, т. е. 
и направлена перпендикулярно кривошипу в сторону движения точки А. Ускорение точки А по величине равно произведению квадрата угловой скорости кривошипа также на его радиус, т. е. 
и направлено от точки А к точке О, так как совпадает с нормальной составляющей полного ускорения точки А из-за равенства нулю тангенциальной составляющей ускорения (угловое ускорение кривошипа принимается равным нулю). Точка А принадлежит не только кривошипу, но и шатуну 2 и принимается в качестве полюса относительного вращения точки В. Скорость точки В определяется векторным равенством 
, т. е. скорость точки В равна скорости точки А плюс скорость точки В относительно точки А. В этом равенстве первое слагаемое правой части известно по величине и по направлению, второе слагаемое направлено перпендикулярно шатуну 2 в данном положении, т. е. известно по направлению, и, наконец, вектор левой части направлен параллельно направляющим ползуна. При этих условиях треугольник скоростей легко строится в предварительно выбранном масштабе 
.
Построение плана ускорений производится в той же последовательности, что и план скоростей. При этом используется векторное равенство 
, в котором первый вектор правой части известен полностью, второй неизвестен ни по величине, ни по направлению. Вектор левой части известен по направлению – он направлен параллельно направляющим ползуна. В этих условиях треугольник ускорений не строится. Разложим вектор относительного ускорения на две составляющих, согласно равенству 
. Первое слагаемое представляет собой относительное нормальное ускорение, направленное от точки В к точке А и равное по величине частному от деления квадрата относительной скорости на длину шатуна, т. е. 
. Второе слагаемое, относительное тангенциальное ускорение направлено перпендикулярно шатуну 2 и неизвестно по величине. Теперь план ускорений строится без затруднений с применением заранее выбранного масштаба 
. Планы скоростей и ускорений данного механизма представлены на рис. 4.3.
Используя планы, легко найти физические величины скоростей и ускорений, для этого необходимо измерить отрезки в миллиметрах, выражающие скорости и ускорения, и умножить их на соответствующий масштаб.
Абсолютная скорость точки В: 
, 
.
Относительная скорость точки В: 
, .
Угловая скорость шатуна 2: 
, 
.
Тангенциальное ускорения точки В относительно точки А:
, 
.
Полное относительное ускорение: 
, .
Угловое ускорение шатуна 2: 
, 
.
4.4. Метод кинематических диаграмм
(метод графического дифференцирования)
Основой метода служит известное положение математики, согласно которому производная функции, заданной в виде графика, в какой-либо её точке численно равна тангенсу угла наклона касательной, проведённой в этой точке к графику функции, то есть
.
Так как теория механизмов и машин имеет дело с именованными числами, то при определении величины тангенса необходимо учитывать масштабы по осям координат графика функции (рис. 4.4), тогда
.
Выберем горизонтальный отрезок произвольной длины и проведём из его левого конца наклонную прямую, параллельную касательной, а из правого конца – вертикальную прямую до пересечения с наклонной. Вычислим длину отрезка, полученного на вертикали и обозначенного на рис. 4.4 буквой 
. Построенный треугольник является прямоугольным с углом против вертикального катета, равным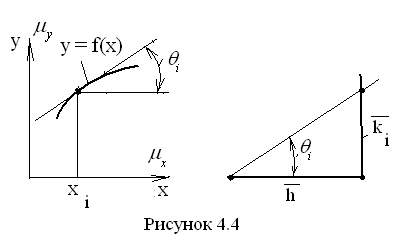 
. Поэтому, записав из треугольника 
и подставив это отношение в предыдущее выражение, получаем
.
В правой части этого выражения переменной величиной является только 
, остальные образуют постоянное число, которое можно считать масштабом, то есть
.
Таким образом мы убедились, что отрезок в масштабе 
выражает производную в данной точке графика.
Для применения рассмотренной методики необходимо предварительно построить график или функции положения механизма, или график аналога скорости. Чтобы построить график производной, необходимо на продолжении оси абсцисс этого графика в левую сторону от оси ординат выбрать произвольный отрезок 
и на нём строить все треугольники, необходимые для определения отрезков . Все эти отрезки получаются на оси ординат, но каждый из них необходимо разместить на ординатной прямой соответствующего номера, а их концы соединить плавной кривой. Эта процедура даст искомый график.
Вопросы для самопроверки
1. Сформулируйте задачи кинематического анализа механизмов с низшими парами.
2. Перечислите методы исследования кинематики механизмов.
3. Что должно быть задано для исследования кинематики механизма?
4. В чём заключается сущность аналитического метода исследования кинематики?
5. Что называется масштабом в ТММ?
6. Что такое разметка механизма?
7. Для чего строится разметка?
8. Как определяются скорость и ускорение конца кривошипа?
Рекомендуем посмотреть лекцию "6 - Биотические регионы суши".
9. Запишите векторные уравнения для построения планов скоростей и ускорений и объясните их составляющие. Какое правило механики положено в основу этих уравнений?
10. Как определяются скорости и ускорения центра масс шатуна?
11. Как определить угловые скорость и ускорение стержневого звена?
12. Какое правило математики положено в основу графического дифференцирования функции, заданной в виде графика?
13. Приведите пример построении графика производной при заданном графике функции.
14. Как определяются масштабы по осям координат при построении графика производной?
